1. Численное интегрирование: вывод формулы прямоугольников и оценки погрешности.

Постановка задачи: дано , требуется найти приближённое значение интеграла : , - заданная точность.

Актуальность задачи: - f(x) вычисляется «сложно» из эксперимента

- f(x) задана таблицей своих значений.

Задача интерполяции: y(x) – задана таблично

- глобальная интерполяция

- m+1 узел, - кусочно-полиномиальная интерполяция .

Основная идея построения формул интерполяционного типа:

, - такова, что интеграл вычисляется, .

Простейшие формулы численного интегрирования:

; - узлы квадратурной формулы, ;

- элементарный отрезок интегрирования; - составной отр. инт-я;

- числовые коэффициенты – веса квадратурной формулы.

- квадратурная сумма (формула).

Величина - называется погрешностью (или остаточным членом) квадратурной формулы.

Будем говорить, что квадратурная формула точна для многочленов степени m, если для любого многочлена степени не выше m эта формула даёт точное решение интеграла, т.е.

Формула левых прямоугольников:

- априорная оценка погрешности, .

Формула правых прямоугольников:

; ; .

Формула центральных прямоугольников:

; ; .

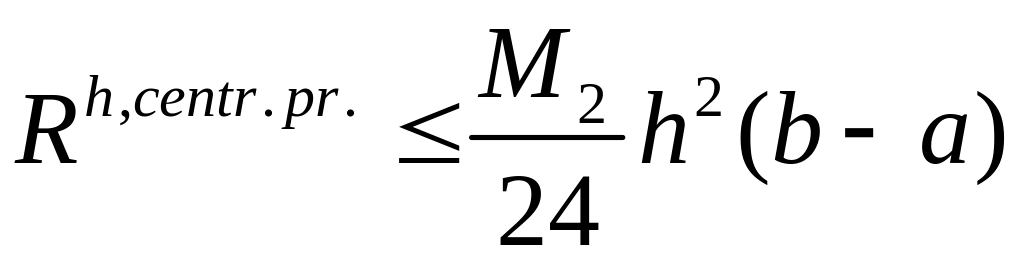Вывод оценки интерполяции: условие: f – дважды непрерывно дифференцируема.

Представим погрешность формулы в виде:

Используя формулу Тейлора: ,

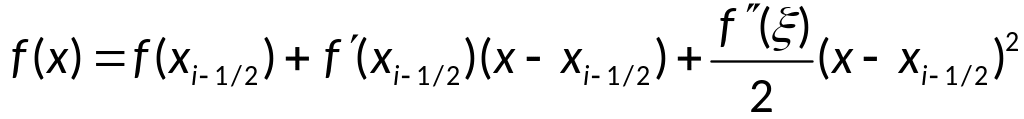где , имеем:

;

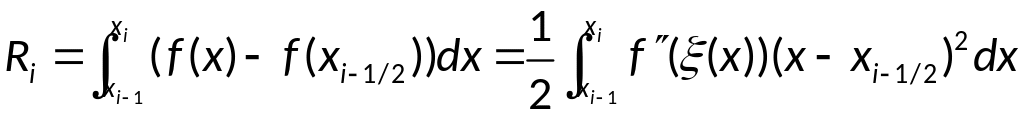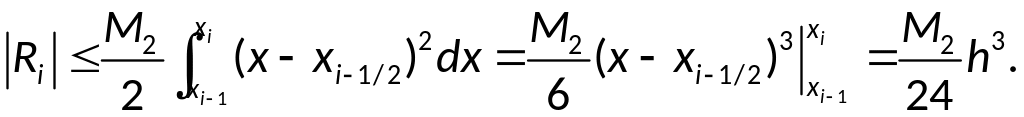
Так как , то

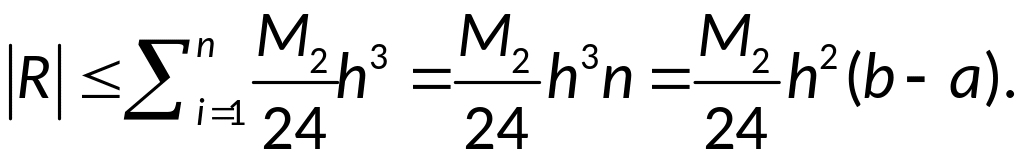
2. Численное интегрирование: вывод формулы трапеций и оценки погрешности.

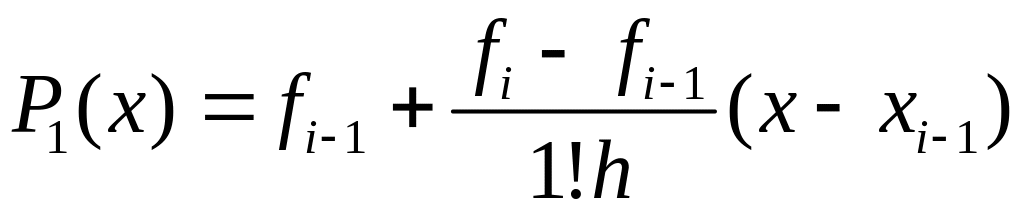; - многочлен Ньютона.

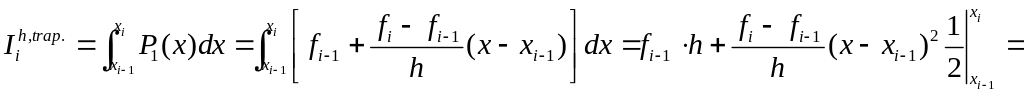
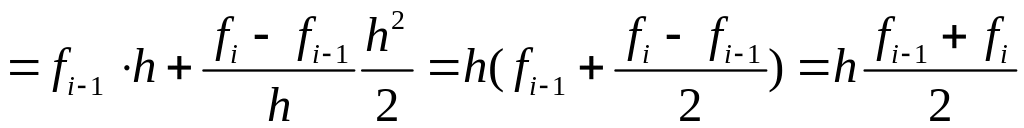- элементарная формула трап.

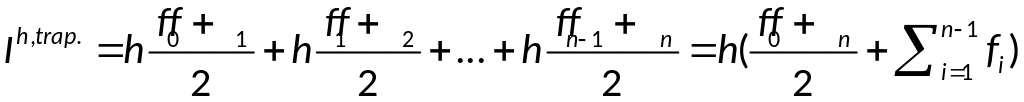- составная ф-ла.

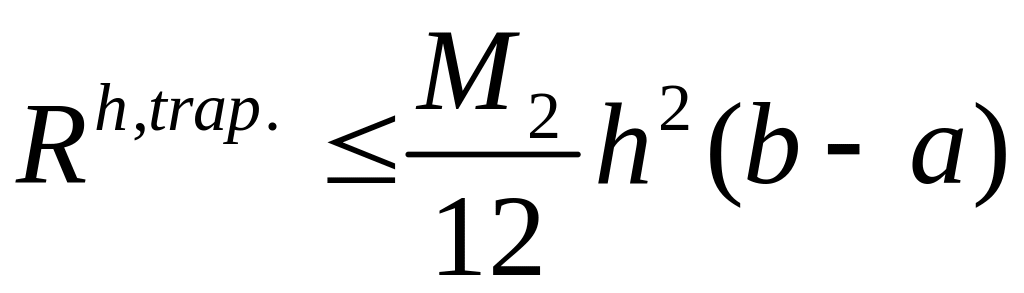- априорная оценка.

Для вывода оценки воспользуемся тем, что отрезок, соединяющий две соседние точки, представляет собой график интерполяционного многочлена первой степени

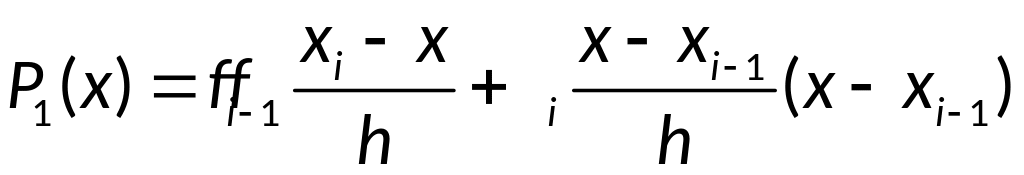. Поэтому для элементарной формулы трапеций верно равенство: .

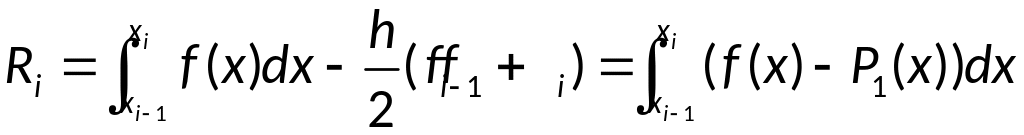Используя оценку погрешности линейной интерполяции, имеем:

, следовательно, для справедлива оценка:

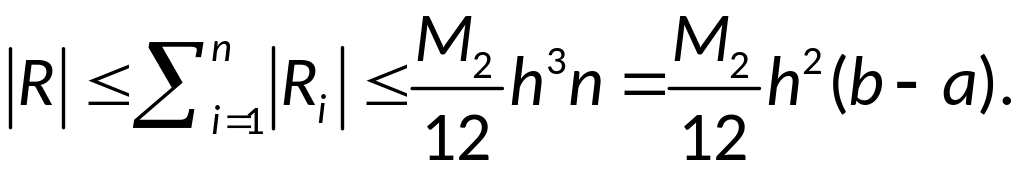
3. Численное интегрирование: формула Симпсона и оценка погрешности.

Если площадь элементарной криволинейной трапеции заменить площадью фигуры, расположенной под параболой, проходящей через точки , то получим приближённое равенство , - интерполяционный многочлен второй степени.

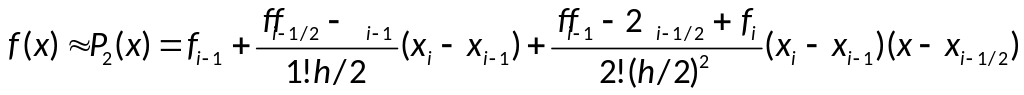
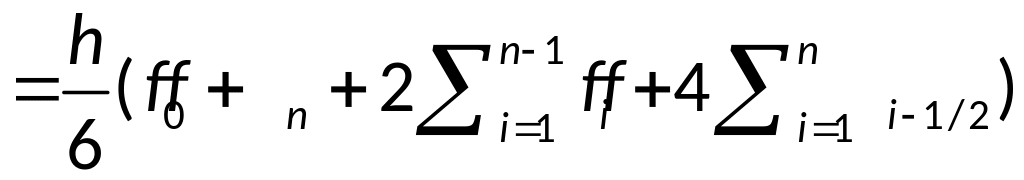- элементарная квадратурная формула Симпсона.

- составная формула Симпсона.

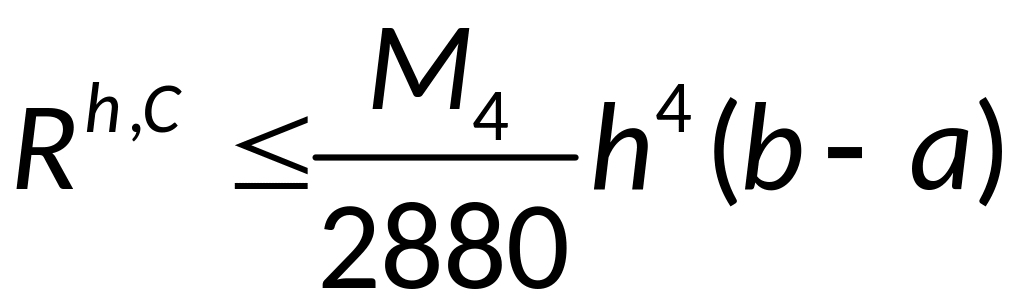- априорная оценка погрешности формулы Симпсона, при условии, что функция f имеет на отрезке [a,b] непрерывную производную четвёртого порядка.

4. Правило Рунге оценки погрешностей. Уточнение по Рунге.

Дано , - квадратурная сумма (приближённое значение интеграла). .

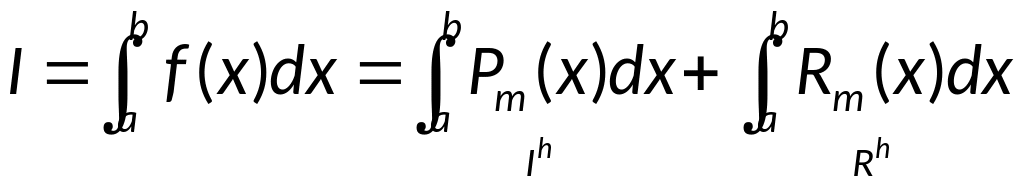
Опр. Квадратурная формула имеет порядок точности .

Правило Рунге: (правило двойного пересчёта) – для практической оценки погрешности (апостериорное правило).

Вычитая из второго первое получаем:

Окончательно получаем: 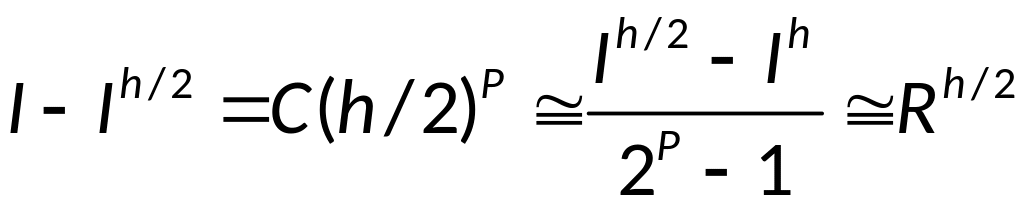- правило Рунге.

Уточнение по Рунге: 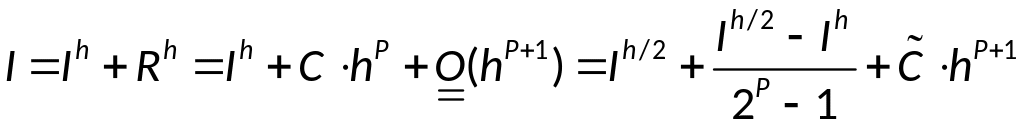главный член погрешности становится точнее.

Для того, чтобы сделать уточнение по Рунге для формулы трапеции с шагом h, нужно: записать формулу трапеции с половинным шагом, в результате получим формулу Симпсона при шаге интерполяции h.

Опр. Пусть квадратурная формула применяется для многочленов степени m и пусть значения интегралов для всех многочленов степени являются точными, а интеграл от многочлена степени m+1 вычисляется приближённо, тогда: квадратурная формула называется формулой алгебраической степени точности m.