19.Решение задачи Коши для уравнения m-го порядка.

Задача Коши для дифф. ур-ния m-го порядка состоит в нахождении ф-ции y(t), удовлетворяющий при дифф. уравнению а при - начальным условиям , Рассмотрим ф-ции , Заметим, что . Поэтому введенные ф-ции удовлетворяют системе дифф. ур-ний первого порядка

20. Многошаговые методы. Вывод формул явного метода Адамса-Башфорта. Порядок аппроксимации метода.

Метод Адамса:

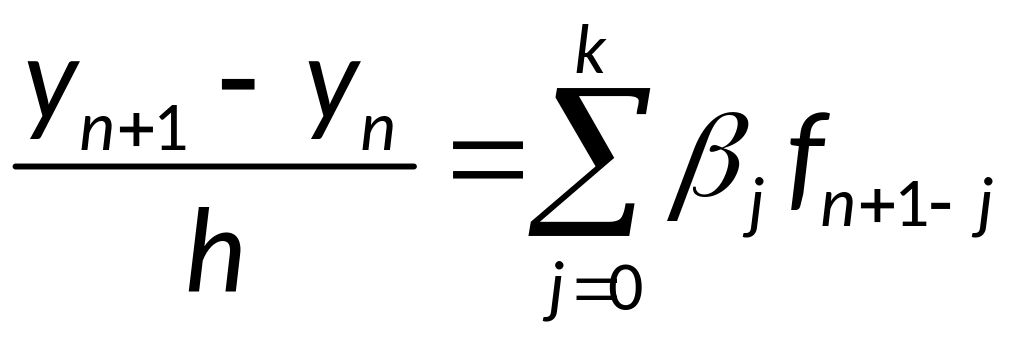, где - числовые коэффициенты, .

Это уравнение позволяет найти новое значение , использовав найденные ранее значения . Поэтому предварительно требуется задание k начальных значений .

Выведем формулу явного метода Адамса-Башфорта:

Из равенства:

Заменим приближенно функцию интерполяционным многочленом (k-1)-й степени , принимающим значения , в тех узлах , где значения сеточной функции уже найдены. Интегрирование этого многочлена дает приближенное равенство .

Получаем формулу 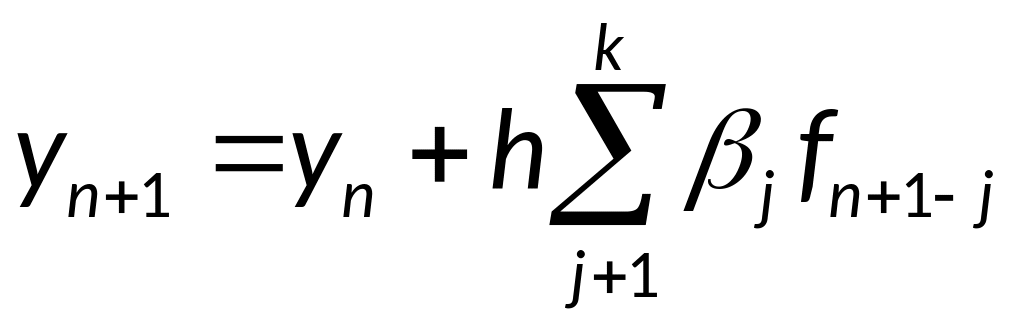, соответствующую явному k-шаговому методу Адамса-Башфорта.

Замечание1: Все это соответствует явному методу Адамса при , т.к. значение выражается через найденные ранее значения по явной формуле.

Замечание2: Иногда его называют экстраполяционным методом.

Замечание3: Двухшаговая формула Адамса-Башфорта:

Порядок аппроксимации:

Пусть решение задачи Коши y(t) непрерывно дифференцируемо k раз на отрезке . Тогда k-шаговый метод Адамса-Башфорта имеет порядок аппроксимации равный k.

21. Многошаговые методы. Вывод формул неявного метода Адамса-Моултона. Порядок аппроксимации метода.

Метод Адамса:

, где - числовые коэффициенты, .

Это уравнение позволяет найти новое значение , использовав найденные ранее значения . Поэтому предварительно требуется задание k начальных значений .

Выведем формулу явного метода Адамса-Моултона:

Из равенства: 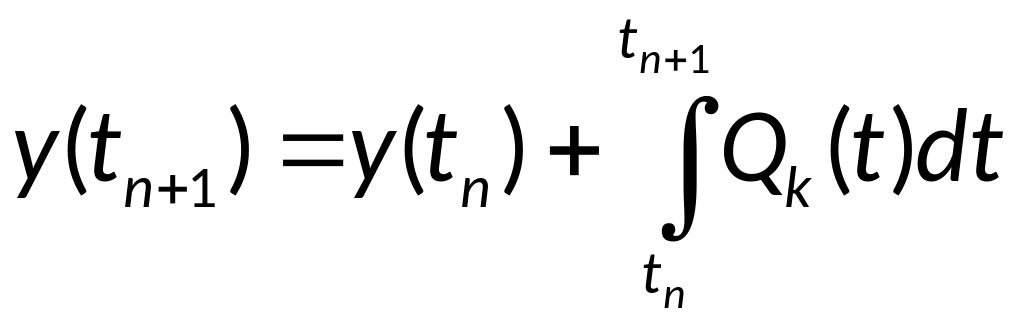, где - интерполяционный многочлен k-й степени, совпадающий со значениями в узлах , то получится формула: 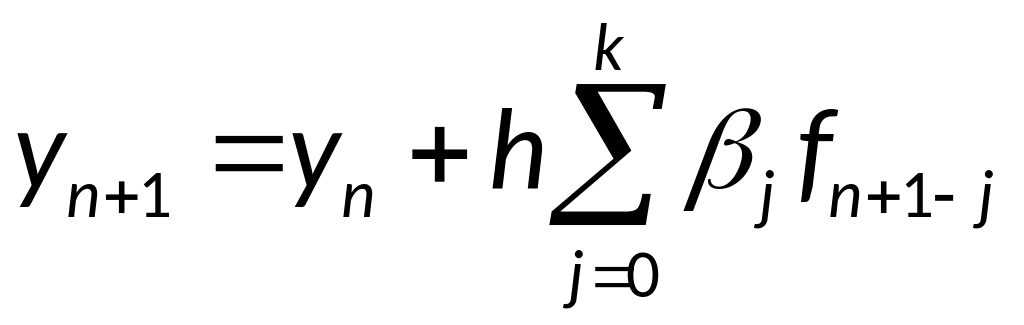, соответствующая k-шаговому методу Адамса-Моултона. Заметим, что этот метод-неявный.

Замечание1: Все это соответствует неявному методу Адамса при .

Замечание2: Иногда этот метод называют интерполяционным методом Адамса-Моултона.

Замечание3: Одношаговая формула Адамса-Моултона: .

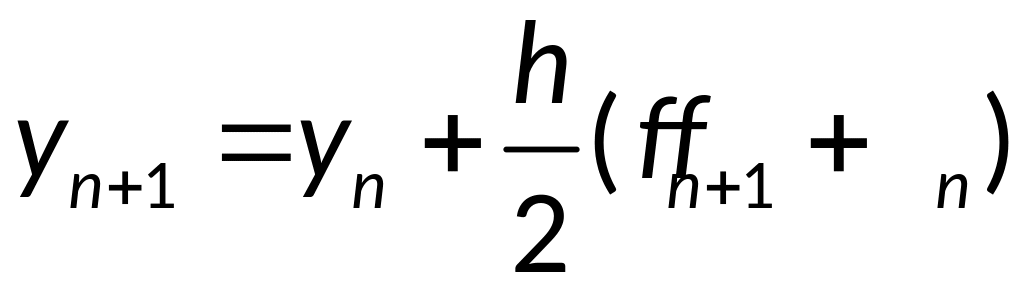Порядок аппроксимации:

Пусть решение задачи Коши y(t) непрерывно дифференцируемо k раз на отрезке . Тогда (k-1)-шаговый метод Адамса-Моултона имеет порядок аппроксимации равный k.

22. Устойчивость численных методов. Понятие нуль-устойчивости.

Примем дискретное решение: , где - решение дискретной задачи при , а - решение дискретной задачи при . При этом зададим фиксированный шаг h, известен отрезок , на котором ищется решение, а погрешность ( ), то погрешность значение можно оценить:

-обусловленность метода, от Т и h.

Нуль устойчивость:

Сразу заметим, что коэффициент может неограниченно возрастать при , а уменьшение шага h приведет не к уточнению решения, а, наоборот, к неограниченному росту погрешности.

Таким образом примем: , где не зависит от h.

Методы, для которых неравенство будет выполняться, когда решается задача Коши для однородного уравнения , будем называть нуль-устойчивыми.

Чтобы отбросить те из методов, которые заведомо не обладают свойством нуль-устойчивости, применим дискретный метод к решению задачи Коши для уравнения . Тогда : , при ,будем называть их линейными однородными разностными уравнениями k-го порядка с постоянными коэффициентами. Пусть решение того же уравнения, тогда в силу линейности уравнения погрешности : (1)

Заменив и сократив на общий множитель получим: -характеристическое уравнение, которое должна удовлетворять величина q.

Пусть q-корень ранее записанного уравнения, тогда сеточная функция является решением разностного уравнения (1). Запишем структуру общего решения разностного уравнения: -корни характеристического уравнения, -их кратности( ), тогда:

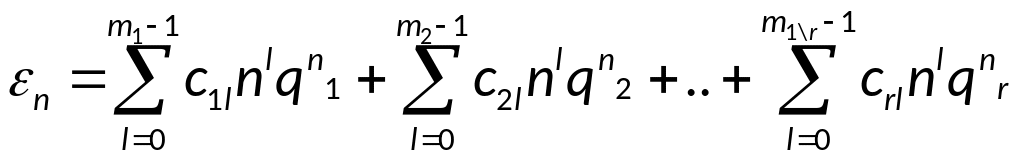
Если -не кратные:

Будем говорить, что выполнено корневое условие, если все корни характеристического уравнения лежат внутри или на границе единичного круга комплексной плоскости(т.е. ), причем на границе единичного круга нет кратных корней.

Теорема: Для того чтобы метод обладал нуль-устойчивостью, необходимо и достаточно, чтобы выполнялось корневое условие.

Замечание1: Для дискретного метода q=1, всегда является корнем характеристического уравнения.

Замечание2: Всегда нуль-устойчивы: все методы Рунге-Кутты и Адамса.

Х. Устойчивость численных методов. Понятие абсолютной устойчивости.

Дискретные методы решения задачи Коши: 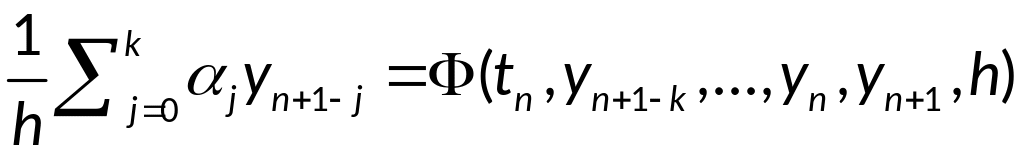(1)

Пусть -решение дискретной задачи, соответствующее начальным значениям , а - решение той же задачи, соответствующее начальным значениям .Если погрешности задания начальных данных достаточно малы, то погрешность значения можно оценить следующим образом: , величина К играет роль числа обусловленности метода.

Значит.часть заведомо непригодных для решения задачи коши на больших временных отрезках методов можно исключить, исследуя результат их применения к реш. модельной задачи:

,

Большинство дискретных методов становятся линейными и приобретают вид:

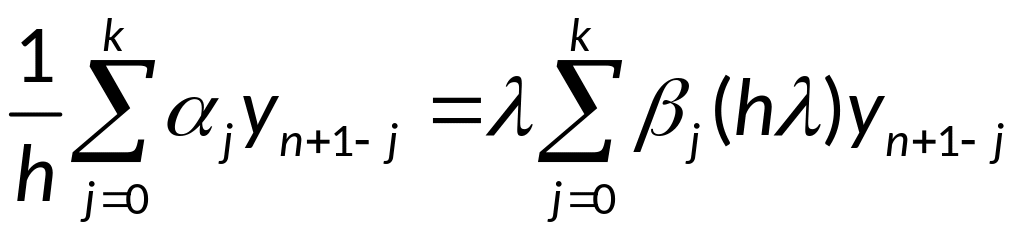
Здесь -некот. зависящие от величины функции. В силу линейности ошибка удовлетворяет тому же уравнению

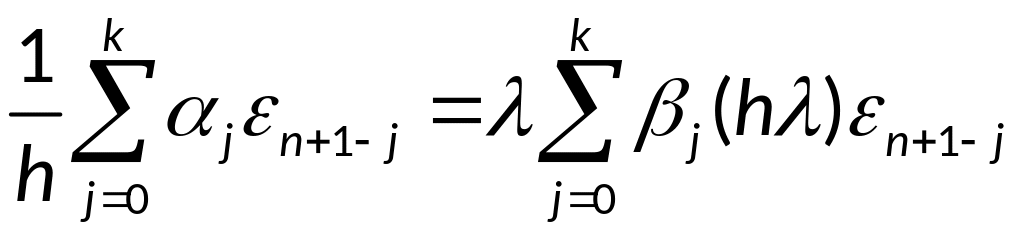
Перепишем в виде: , где ,

Назовем метод (1) абсолютно устойчивым для данного , ежели при этом Z все корни полинома устойчивости 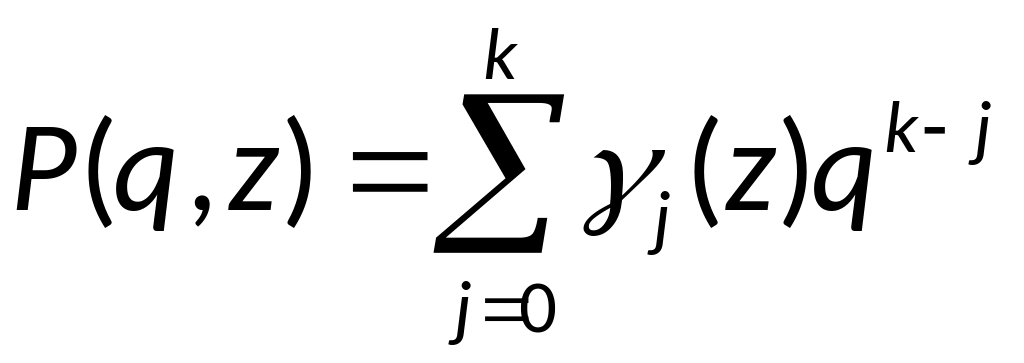лежат в комплексной плоскости внутри единичного круга и на границе этого круга нет кратных корней. Множество D точек комп. Плоскости, состоящие из тех z, для которых метод абс.устойчив, называют областью абсолютной устойчивости метода.