6. Математические модели непрерывных систем в комплексной области.

Одностороннее непрерывное преобразование Лапласа: передаточная функция (ПФ), преобразование Фурье (частотная характеристика). 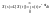, x(t) – оригинал, X(s) – изображение.

1) y(t)=ax(t), a=const, только линейные системы. Y(s)=aX(s).

2) y(t)=x₁(t)+x₂(t), Y(s)=X₁(s)+X₂(s)/

₃₎

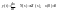
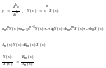
_{ПФ – отношение преобразованных по Лапласу при 0 входных условиях выходного сигнала к входному}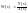

ЧХ – формулы и графики, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме.

На вход: x(t)=sinωt, на выходе: y(t)=A(ω)sin(ωt+φ)/

7. Модели систем при последовательном согласном соединении звеньев.

Последовательным соединением звеньев называется такое соединение, при котором выходная величина предыдущего звена поступает на вход последующего.

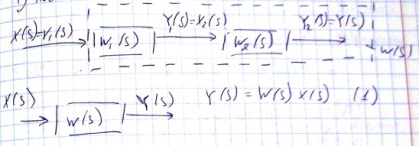
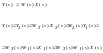
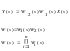
Сохраняет и устойчивость и минимальнофазовость: если звенья все таковы, то и система тоже. Если хотя бы одно звено не- и не-, то и вся система становится такой.

Частотные характеристики:

АЧХ: ;

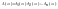ФЧХ: .

8. Модели систем при параллельном согласном соединении звеньев.

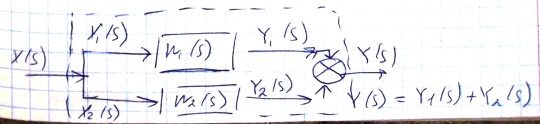
При этом выполняются соотношения и , то есть изображение выходной величины определяется как сумма изображений выходных величин отдельных звеньев.

Если хотя бы одно звено неустойчиво, то и вся система становится неустойчивой. Свойство минимальнофазовости не сохраняется.

9. Модели систем при параллельном встречном соединении звеньев.

Для определенности рассматривается схема, когда звено K₁(s) охватывается отрицательной обратной связью с помощью звена K₂(s).

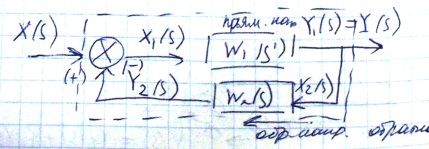
Звено 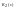- звено обратной связи. Чаше обозначается как .

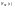Звено 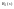- звено прямого тракта. Обозначается - 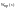. Обратная связь в соединениях может быть положительной (X₁(s)=X(s)+Y₂(s)) и отрицательной (X₁(s)=X(s)-Y₂(s)).

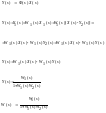
Свойство устойчивости не сохраняется, минимальнофазовости – сохраняется.

10. Понятие об устойчивости. Основная теорема устойчивости для линейных непрерывных систем.

Под устойчивостью, или (более корректно) под устойчивостью процессов управления, понимается работоспособность, т. е. способность системы в принципе отрабатывать входные воздействия.

Для исследования свойств устойчивости вводится в рассмотрение ошибка , где x(t) – входное (задающее) воздействие; y(t) – выходная переменная. Требованием соблюдения устойчивости является выполнение в переходном режиме условия: .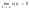

В теории управления доказана основная теорема устойчивости, в соответствии с которой для устойчивости линейной системы необходимо и достаточно, чтобы корни характеристического уравнения 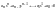имели бы отрицательные вещественные части

Аналитически условия теоремы соответствуют выполнению неравенств:

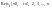
Существует и другая формулировка основной теоремы. Для этого вводится в рассмотрение комплексная плоскость корней: система устойчива при условии, если все ее корни располагаются в левой полуплоскости. Попадание хотя бы одного корня в правую полуплоскость означает неустойчивость системы управления (расходящийся характер переходных процессов). Мнимая ось в общем случае является колебательной границей устойчивости и при нахождении на ней хотя бы одной пары мнимых корней в переходном режиме устанавливаются незатухающие колебания. Начало координат соответствует апериодической границе устойчивости.