11. Алгебраические критерии устойчивости. Критерий Рауса-Гурвица.

Под критериями понимают методы оценки устойчивости, не связанные непосредственно с нахождением корней.

D(s)=a_nsⁿ+ a_n-1s^n-1+ a_n-2s^n-2+…+a₁s+a₀, где n – порядок системы. Определитель Гурвица ∆_n – матрица размером (nxn).

Доказана и существует следующая формулировка критерия: для устойчивости линейной системы достаточно, чтобы при все диагональные миноры в определителе Гурвица были положительными .

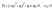
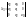
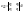
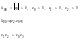
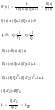
k – коэффициент передачи, система устойчива при k<k_ГР.

∆_n=a₀∆_n-1=0

1) a₀=0, D_n(s)=sD_n-1(s): s₁=0 – апериодическая граница устойчивости.

2) ∆_n-1=0 – колебательная граница устойчивости, a₀=k=0 – апериодическая граница устойчивости.

11. Принцип аргумента. Частотный критерий Михайлова.

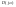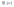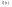Под годографом понимается кривая, которую описывает конец вектора или на комплексной плоскости при изменении  от 0 до . Здесь и - полиномы знаменателей соответствующих передаточных функций.

A(s)=a_nsⁿ+ a_n-1s^n-1+ a_n-2s^n-2+…+a₁s+a₀

Характерной особенностью данного метода является то, что об устойчивости системы судят по поведению годографа Михайлова исследуемой системы:

_{1) А(s)=Q(s) – для разомкнутой системы;}

_{2)A(s)=D(s) – замкнутой.}

_{A(s)=an(s-s1)…(s-sn), si→A(si)=0,}

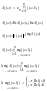
A(jω)=D(jω) – замкнутая САУ. В соответствиии с основной теоремой устойчивости все корни характеристического уравнения: D(s_i)=0, ReS_i<0, 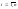, m=0, l=n.

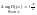- критерий устойчивости Михайлова

На основании принципа аргумента формулируется критерий Михайлова:

Для устойчивости системы необходимо и достаточно, чтобы годограф вектора Михайлова для замкнутой и для разомкнутой системы) при изменении  от 0 до + повернулся в положительном направлении на угол (/2)n или, иначе, пересек по очереди n квадратов без пропусков.

Все эти годографы (и системы соответственно) устойчивы.

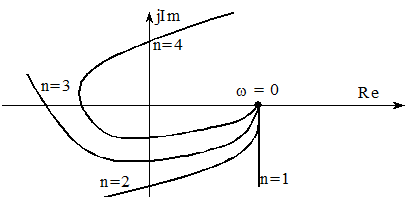
Эти системы неустойчивы, так как вектор годографа Михайлова вращается в отрицательном направлении.

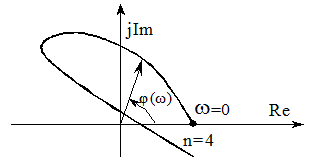
Система неустойчива, так как квадранты проходятся непоследовательно.

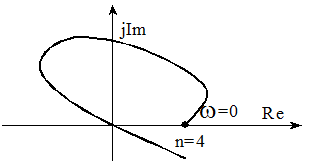
Система находиться на границе устойчивости. При подсчете порядка системы каждое прохождение годографа через 0 повышает порядок на 1.

Следствие из критерия Михайлова:

Для устойчивости системы необходимо и достаточно, чтобы корни мнимой и вещественной частей годографа Михайлова перемежались. Если корни не перемежаются, то система неустойчива. Если характеристическое уравнение не имеет какого либо члена, то система также неустойчива.

11. Критерий устойчивости Найквиста (три случая).

Частотный критерий Найквиста дает возможность определить устойчивость замкнутой системы по АФЧХ ее разомкнутой цепи (разомкнутой системы) .

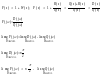
Различают три возможных ситуации:

1. не содержит правых или нулевых корней, то есть разомкнутая система устойчива.

Для устойчивости замкнутой системы, устойчивой в разомкнутом состоянии необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы при изменении от 0 до не охватывал критическую точку с координатой ( ).

.

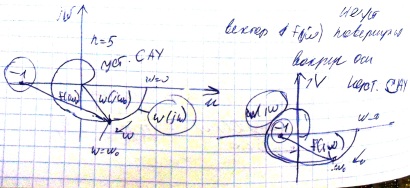
2. имеет хотя бы один правый корень, следовательно, система в разомкнутом состоянии неустойчива.

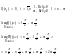
Следовательно, для устойчивости замкнутой системы, неустойчивой в разомкнутом состоянии, необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы при изменении  от 0 до , двигаясь в положительном направлении (против часовой стрелки), 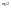раз охватил критическую точку 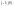_{, где m1 – число правых корней}.

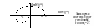
3. Все корни левые, но есть и корни на мнимой оси (на границе устойчивости).

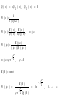
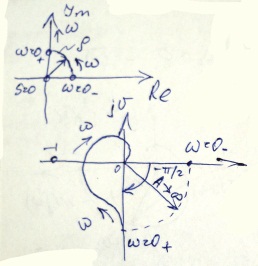
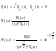
Вывод. Для устойчивости замкнутой системы, имеющем в разомкнутом состоянии все левые точки, а также 1 или несколько нулевых корней, необходимо и достаточно, чтобы при изменении  от 0 до критическая точка не охватывалась годографом АФЧХ разомкнутой системы вместе с ее дополнением.

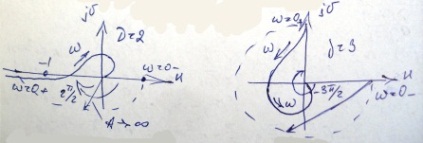
Дополнением является дуга с , повернутая от оси вещественных корней на угол .
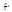