
- •1)Свойства определённого интнграла. Вычисление определённого интеграла. Теорема Ньютона-Лейбница
- •2)Интегрирование по частям.
- •3. Вычисление площади криволинейного сектора.
- •4.Вычисление длины дуги кривой. Площадь поверхности тела вращения. Вычисление объёмов тел
- •5)Криволинейный интеграл I рода. Криволинейный интеграл II рода
- •6)Свойства криволинейного интеграла 2 рода.Формула Остроградского-Грина
- •7. Условия существования двойного интеграла
- •8. Вычисление двойного интеграла
- •9.Определние. Замена переменных в тройном интеграле.
- •10. Цилиндрическая система координат. Сферическая система координат.
- •11.Свойства рядов
- •12.Признак Даламбера
- •13. Признак Лейбница. Признаки Доламбера для знакопеременных рядов.
- •14. Признак Коши для знакопеременных рядов. Свойства абсолютно сходящихся рядов
- •15. Функциональные ряды. Свойства равномерно сходящихся рядов. Степенные ряды.
- •1) Теорема о непрерывности суммы ряда.
- •2) Теорема о почленном интегрировании ряда.
- •3) Теорема о почленном дифференцировании ряда.
- •16)Для того чтобы найти область сходимости ср., докажем теорему Абеля.
- •1) Интегрирование степенных рядов.
- •17.Ряды фурье. Тригонометрический ряд.
- •18.Достаточные признаки разложимости в ряд Фурье. Разложение в ряд Фурье непериодической функции.
- •19.Ряд Фурье для четных и нечетных функций
- •20.Интеграл Фурье
- •21.Свойства функции комплексного переменного
- •22.Производная функций комплексных переменных.
- •23. Свойства векторов. Линейная зависимость векторов.
- •24. Скалярное произведение векторов.
- •25 Векторное произведение векторов
- •26 Смешанное произведение векторов
- •32.Операция умножения матриц.
- •33. Элементарные преобразования. Миноры
- •34. Обратная матрица
- •35. Метод Крамера
- •36. Метод Гаусса
- •37. Определение. Уранением линии
- •38 Уравнение прямой по точке и вектору нормали
- •41. Нормальное уравнение прямой:
- •42. Уравнение прямой проходящей через данную точку перпендикулярно данной прямой:
- •43 . Уравнение окружности и эллипсиса
- •44. Уравнение гиперболы
- •45. Уравнение параболы
- •46.Полярная система координат
7. Условия существования двойного интеграла
Так
как область интегрирования производится
произвольным выбором точек
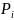 , то считается что все площади одинаковы.
, то считается что все площади одинаковы.
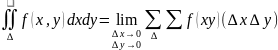
Достаточные условия существования двойного интеграла
Т.:
Если функция f(x,y)
непрерывна в замкнутой области
 , то
, то
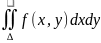 существует.
существует.
Т.: Если функция f(x,y)ограниченна в замкнутой области и непрерывна в ней всюду, кроме конечного числа кусочно гладкой линии, то двойной интерграл существует.
Свойства:

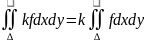
Если
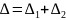 и
и
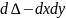 следовательно
следовательно
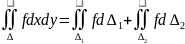
Теорема о среднем:
Двойной интеграл от функции f(x,y) равен произведению значений этой функции в некоторой точке области в области интегрирования на интеграл принадлежащий этой области
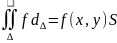
5.Если
f(x;y)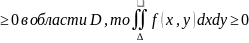
6.Если
f1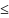 f2
то
f2
то
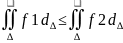
7.|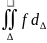 |
|
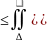
Если
функция f(x,y)
непрерывна в области
,ограниченной
линиями x=a,x=b
при a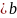 ,y=
,y=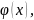
Y=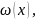 где
где
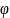 и
и
 непрерывные функции.
непрерывные функции.
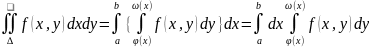
Если
функция
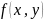 непрерывна в замкнутой области
,ограничена
линиями y=c,y=d
(c
непрерывна в замкнутой области
,ограничена
линиями y=c,y=d
(c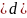
X=Ф(y),x
=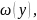 (Ф(y)
(Ф(y)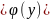
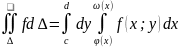
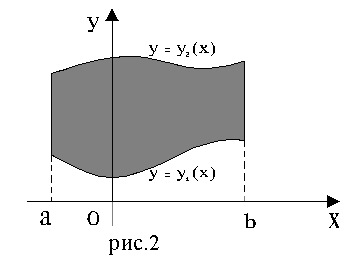
8. Вычисление двойного интеграла
Т.:
Если функция f(x,y)
непрерывна в замкнутой области
ограниченная двумя линиями x=a
, x=b,
a<b,
y=
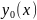 ,
y=
,
y=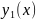 , где
, где
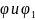 непрерывны и
непрерывны и
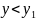 .
.
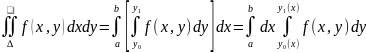
Т.:
Если функция f(x,y)
непрерывна в замкнутой области
граниченная линиями y=c,
y=d
, c<d
, x=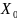 (y),
x=
(y),
x=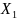 (y)
(y)
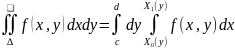
Замена переменных в двойном интеграле
Двойной
интеграл вида
 , где x
, где x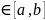 , а y
, а y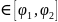
X=f(u,
v),
y=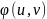 тогда
тогда
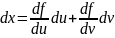 и
и
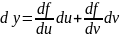
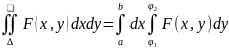
Так
как при первом интегрировании x
применяется за const
dx=0
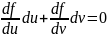
du=
-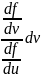
dy
= -
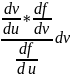 +
+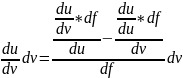
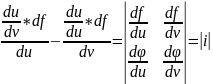
Определитель Якоби
=
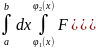 dv
dv
При первом интегрировании выражение для dx примет вид, предполагая, что
v=const
dv=0
, dx
=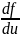 du
при изменении порядка интегрирования,
получим
=
du
при изменении порядка интегрирования,
получим
=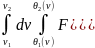
9.Определние. Замена переменных в тройном интеграле.
Тройным интегралом от функции f(x, y, z) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):
![]()
Пример:
![]() Сделаем
замену:
Сделаем
замену:
![]()
Область интегрирования U' в новых переменных u, v, w ограничена неравенствами
![]()
![]()
Вычисляя якобиан, получаем:
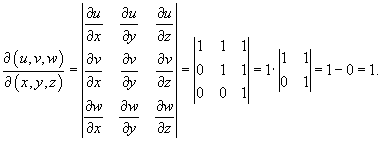
![]()
![]()
10. Цилиндрическая система координат. Сферическая система координат.
Цилиндрическая система координат.
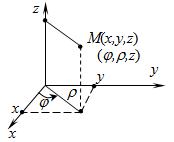
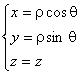
![]()
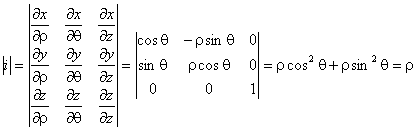
![]()
Сферическая система координат

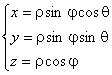
![]()

11.Свойства рядов
Сумма
членов бесконечной числовой
последовательности u1,u2,…..un
– называется числовым рядом и обозначается
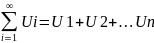
Суммы
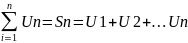 –называются частными суммами ряда
–называются частными суммами ряда
Если
ряд сходятся ,то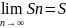 ,
S=
,
S=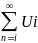
Если последние части сумм ряда расходятся, т.е не имеет предел или он бесконечен, то ряд называется расходящимся и ему не ставят соответственно никакой суммы
Свойства рядов:
1)сходимость или расходимость ряда не нарушится ,если изменить(отбросить или добавить) конечное число членов
2) ∑Un, ∑CUn
Если ряд Un сходится и его сумма равна S, то и ∑СUn сходится , и его ∑=С*Sn(C≠0)
3) ∑Un, ∑Vn
Суммой или разностью этих рядов будет - называется следующий ряд ∑( Un±Vn ), где элементы полученные в результате сложения или вычитания исходных элементов с одинаковым номеров
Теорема:
Если ряды ∑Un , ∑Vn сходятся и их суммы соответственно S и X,то ряд ∑(Un±Vn) также сходится и его сумма равна S±X
Разность 2х сходившихся рядов также является сходящейся.
Сумма сходящихся и расходящихся рядов является расходящимся рядом.
О сумме 2х расходящихся рядов общим утверждением сказать нельзя.
Критерий Коши.
Для
того чтобы последовательность а1,а2….аn
была сходящейся необходимо и достаточно,
чтобы для любого Ƹ>0 существует номер
N,что
при n>N
и для любого р>0,где p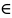 Z
выполняется следующее равенство |an₊p-
an|<Ƹ
Z
выполняется следующее равенство |an₊p-
an|<Ƹ
Доказательство:
Необходимость
an
a
для любого Ƹ>0 найдется номер N,что
неравенство |a
– an|<
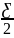 при n>N
при n>N
При этом же условии и для любого p Z>0
|a - an₊p| <
|an₊p-
an|=
(an₊p-
a)+(
a
– an)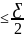 +
=Ƹ
критерий для ряда
+
=Ƹ
критерий для ряда
Для
того чтобы
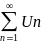 был сходимым необходимо и достаточно
чтобы для любого Ƹ>0 существовал номер
N
, n
> N
и для любого p>0
выполняется следующее неравенство
был сходимым необходимо и достаточно
чтобы для любого Ƹ>0 существовал номер
N
, n
> N
и для любого p>0
выполняется следующее неравенство
|Un₊1+ Un₊2+…+Un₊p|<Ƹ
|Sn₊p –Sn|<Ƹ
На практике используются другие признаки:
Если ряд сходится ,то необходимо чтобы общий член ряда стремился к 0. Однако данное условие не является достаточным. Если общий член не стремится к 0,то ряд однозначно расходится.
Если ряд сходится, то последовательность его частичных сумм ограничена.
Ряды с неотрицательными членами.
Для сходимости ряда с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.
Пусть
даны Un
и Vn,
Un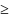 0
,Vn
0
0
,Vn
0
Теорема: если Un Vn при любых n ,то из сходимости ряда Vn следует сходимость ряда,a из расходимости ряда Un следует расходимость ряда Vn. ∑Un ∑Vn, Sn Xn
Доказательство: так как по условию теоремы ряд Vn сходится, то его частичные суммы ограничены. Т.е при всех Xn M ,где M- некоторое положительное число. Т.к Un меньше Vn отсюда следует Sn Xn .
