1)Свойства определённого интнграла. Вычисление определённого интеграла. Теорема Ньютона-Лейбница

Определенный интеграл и условие его существования.

Если сумма

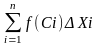
при maxXi стремится к нулю, то имеет место предел независящий ни от способа разбиения отрезка на элементарные, ни от выбора точек на этих отрез­ках. Этот предел называется определенным интегралом функции y(x) на отрезке [a;b] и обозначается =

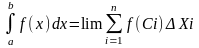(2) в равенстве (2). числа a и b называются нижним и верхним пределами интегрирования. Т. (Коши) Если функция непрерывна на отрезке, то определенный интеграл существует. Эта теорема выражает достаточное условие интегрируемости функции.

Основные свойства определенных интегра­лов.

1)

2) при а<b

3) c=const

4)

5) для произвольных с, при условии интегрируемости функции f(x) (аддитивность интеграла относительно промежутка)

6) если для любого х из интервала [a,b]

Если функции f(x), g(x) принадлежат [a,b], то имеет место неравенство:

7) если для любого x из интервала [a,b]

если g(x)≥0 для любого x из интервала [a,b], где M=sup f(x) – наибольшее , а m = inf f(x) – наименьшее значение функции на промежутке [a,b].

Вычисление определенного интеграла с помощью формулы Ньютона – Лейбница. Известно, что для любой функции f(x), непрерывной на отрезке [a;b], существует на этом отрезке интеграл т.е. 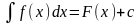F(x) первообразная для функции f(x). Т. Определенный интеграл от непрерывной функции на отрезке равен разности значений любой первообразной от этой функции взятых при нижнем и верхнем пределах интегрирования. 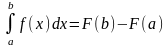(1) Равенство (1) называется формулой Ньютона –Лейбница Если ввести обозначение F(b)-F(a)=F(x)|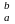 , то формулу (1) можно переписать: 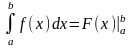Формула Ньютона – Лейбница дает удобный способ вычисления определенного интеграла, чтобы найти определен­ный интеграл на отрезке, надо найти первообраз­ную подынтегральной функции и взять разность ее значений от верхнего и нижнего пределов интег­рирования.

Вычисление определенного интеграла

Замена переменной в определенном интеграле. Пусть требуется вычислить определен­ный интеграл от функции f(x), где f(x) – непре­рывна на промежутке [a;b] предположим, что х есть некая функция от переменной t, т.е. x=(t). Если выполняются следующие условия: 1 x= (t) и ее производная x`=`(t) непрерывна при t  [; ] 2 множество значений функции x=(t) при t  [ ; ]является [a ; b] 3 ()=a, ()=b, то

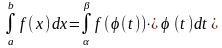(2) Формула (2) - формула замены переменной в определенном интеграле. Формула интегрирования по частям в определенном интеграле. Если функции u(x) и v(x) имеют непрерывное произведение на отрезке [a;b], то имеет место формула:

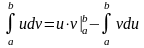
2)Интегрирование по частям.

Данный метод основан на известной фор. произведения

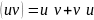
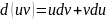
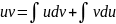
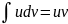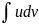- – формула интегр. по частям

Замена переменных.

Если требуется найти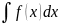 , сложно отыскать первообразную, то с помощью замены 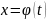и 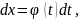получим: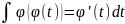

При замене переменной в определенном интеграле вводимая функция должна быть непрерывна на отрезке интегрирования.Иначе абсурд.

Несобственные интегралы

Пусть ф-ия f(x) отделена от а до 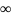,тогда она непрерывна на любом AB.Если существует конечный предел 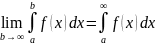говорят что несобственный интеграл сходится.

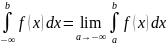
Теорема 1:если для всех x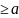 выполняется 0 .

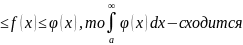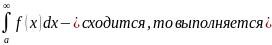
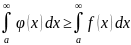
Теорема 2

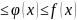Если x 0 и

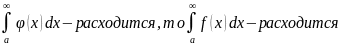
Теорема 3