
- •Вопрос1 Кинематическое описание движения материальной точки
- •Вопрос2 Криволинейное движение
- •Вопрос3 Кинематика вращательного движения
- •Вопрос 4 Законы динамики Ньютона
- •Вопрос 5 Закон сохранения импульса
- •Вопрос 6 Работа, мощность.
- •Вопрос 7 Энергия
- •Вопрос 8 Момент инерции твердого тела
- •Вопрос 9 Работа и кинетическая энергия вращения
- •Вопрос 10 Основной закон динамики вращения
- •Вопрос 11 Закон сохранения момента импульса
- •Вопрос 12 Механические колебания
- •Вопрос 13 Идеальный газ
- •Вопрос 14 Распределение молекул идеального газа по скоростям хаотического теплового движения.
- •Вопрос 15 Распределение молекул в потенциальном поле сил
- •Вопрос 16 Первое начало термодинамики
- •Вопрос 17 Теплоемкость
- •Вопрос 18 Применение первого закона термодинамики к изопроцессам
- •Вопрос 19 Адиабатический процесс
- •2.3.6. Адиабатический процесс. Политропный процесс
- •Вопрос 20 Второе начало термодинамики
- •2.3.8. Энтропия, её статистическое толкование и связь с термодинамической вероятностью
- •2.3.9. Второе начало термодинамики
- •Вопрос 21 Цикл Карно для идеальной тепловой машины Тепловые двигатели и холодильные машины. Цикл Карно и его к. П. Д. Для идеального газа
- •Вопрос 22 Свойства физических зарядов
- •Вопрос 23 Напряженность электрического поля в вакууме
- •Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
- •2. Поле двух бесконечных параллельных равномерно заряженных плоскостей
- •Вопрос 25 Потенциал
- •Вопрос 26 Связь напряженности электрического поля с потенциалом
- •Вопрос 27 Проводники в электрическом поле
- •Вопрос 28 Диэлектрики в электрическом поле
- •Вопрос 29 Энергия электростатического поля
- •Вопрос 30 Постоянный электрический ток
- •Вопрос 31 Закон Ома для однородного участка цепи
- •Вопрос 32 Закон Ома для замкнутой цепи
- •Вопрос 33 Работа и мощность электрического тока
- •Вопрос 34 Магнитное поле в вакууме
- •Вопрос 35 Движение заряженных частиц в магнитном поле
- •Вопрос 36 Взаимодействие магнитного поля с током
- •Вопрос 38 Поток вектора магнитной индукции сквозь произвольную поверхность
- •Вопрос 39 Работа по перемещению проводника и контура с током в магнитном поле.
- •Вопрос 40 Электромагнитная индукция
- •Вопрос 41 Явление самоиндукции
- •Вопрос 42 Энергия магнитного поля тока
- •Вопрос 43 Закон полного тока
- •Вопрос 44 Магнитные свойства вещества
- •Вопрос 45 Магнетики в магнитном поле
- •Вопрос 46 Ферромагнетизм
- •Природа ферромагнетизма
- •Вопрос 50 Интерференция света от двух источников
- •Вопрос 51 Интерференция света в тонких пленках
- •Вопрос 52 Дифракция света
- •Вопрос 53 Дифракция при параллельных лучах Фраунгорфера
- •Вопрос 54 Поляризация света
- •Вопрос 55 Способы получения поляризованного света
- •Вопрос 56 Тепловое излучение
- •Вопрос 57 Законы теплового излучения
- •Вопрос 58 Внешний фотоэффект
- •Вопрос 59 Эффект Комптона
- •Вопрос 60 Корпускулярно – волновой дуализм
- •Вопрос 61 Волновые свойства микрочастиц
- •Вопрос 62 Соотношение неопределенностей
- •Вопрос 63 Волновая функция.
- •Вопрос 64 Боровская теория водородоподобного атома
- •Вопрос 66 Молекула
- •Вопрос 67 Современные представления об электропроводности тел
- •Вопрос 68 Атомное ядро
Вопрос 13 Идеальный газ
Для вывода основного уравнения молекулярно-кинетической теории рассмотрим идеальный одноатомный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку S (рисунок 2.5) и вычислим давление, оказываемое на эту площадку.
При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс
m0v–(–m0v)=2m0v, |
(2.21) |
где m0 – масса молекулы, v – ее скорость. За время t площадки S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием S и высотой vt (рисунок 2.5). Число этих молекул равно nSvt (n – концентрация молекул).
Необходимо учитывать, что реально молекулы движутся к площадке S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул. Половина этих молекул (т.е. 1/6 часть) движется вдоль данного направления в одну сторону, а вторая половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку S будет 1/6 nSvt. При столкновении с площадкой эти молекулы передадут ей импульс
P = 2m0v1/6nSvt = 1/3nm0v2St |
(2.22) |
Тогда давление газа, оказываемое им на стенку сосуда,
P = P/(tS) = 1/3nm0v2. |
(2.23) |
Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2, ..., vN, то целесообразно рассматривать среднюю квадратичную скорость
<vкв>= |
(2.24) |
характеризующую всю совокупность молекул газа. Уравнение (2.23) с учетом (2.24) примет вид
p = 1/3nm0<vКВ>2. |
(2.25) |
Выражение (2.25) называется основным уравнением молекулярно-кинетической теории идеальных газов.
PVm = RT |
|
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона – Менделеева.
В молекулярно-кинетической теории пользуются моделью идеального газа, согласно которой считают, что:
1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Модель идеального газа можно использовать при изучении реальных газов в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах.
Вопрос 14 Распределение молекул идеального газа по скоростям хаотического теплового движения.
Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, т. е. dN(v)/N=(v)dv, откуда
(v)= |
(2.32) |
Применяя методы теории вероятностей, Максвелл нашел функцию f(v)– закон о распределении молекул идеального газа по скоростям:
(v)
= 4
|
(2.33) |
Из (2.33) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры T).
График функции (2.33) приведен на рисунке 2.6.

Рисунок 2.6
Так как при возрастании v множитель exp[-m0v2/(2kT)] уменьшается быстрее, чем растет множитель v2, то функция (v) начинаясь от нуля, достигает максимума при vВ, и затем асимптотически стремится к нулю. Кривая несимметрична относительно vВ.
Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь заштрихованной полоски на рисунке 2.6. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция (v) удовлетворяет условию нормировки
|
(2.34) |
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти, продифференцировав выражение (2.33) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения (v):
|
(2.35) |
Значения v = 0 и v = соответствуют минимумам выражения (2.33), а значение v, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость vВ:
vВ
=
|
(2.36) |
Из формулы (2.36) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рисунок 2.7) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.

Рисунок 2.7
Средняя арифметическая скорость молекулы <v> определяется по формуле
|
(2.37) |
Подставляя сюда f(v) и интегрируя, получаем
|
(2.38) |
Скорости, характеризующие состояние газа:
1) наиболее вероятная
![]() ;
;
2) средняя
![]() ;
;
3) средняя квадратичная
![]() .
.
Исходя из распределения молекул по скоростям
|
(2.39) |
можно найти
распределение молекул газа по значениям
кинетической энергии
![]() .
Для этого перейдем от переменной v
к переменной
.
Для этого перейдем от переменной v
к переменной
![]() .
Подставив в (2.39)
.
Подставив в (2.39)
![]() и
и
![]() получим
получим
|
(2.40) |
где dN () – число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от до +d.
Таким образом, функция распределения молекул по энергиям теплового движения
|
(2.41) |
Средняя кинетическая энергия < > молекулы идеального газа
|
(2.42) |
т.е. получили результат, совпадающий с формулой (2.31).

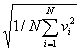 ,
, v2exp[-m0v2/(2kT)]
.
v2exp[-m0v2/(2kT)]
.
 .(
.(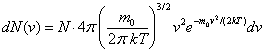 ,
, ,
,