4.Последовательность независимых испытаний. Схема Бернулли. Формула Пуассона.
Пусть проводится серия из n одинаковых испытаний, в каждом из кот. событие А может произойти с одной и той же вероятностью р (в-ть успеха) и не произойти с одной и той же вероятностью q (в-ть неудачи) q=1-p. Наступление либо не наступление события А в n-ом испытании не зависит от исхода предыдущих испытаний.
Pn(m) из n испытаний событие произойдет ровно n раз.
—
формула Бернулли.
Pn(0)+Pn(1)+ Pn(2)+…+ Pn(m)+…+ Pn(n)=(q+p)n=1.
При помощи этой формулы событие произойдет больше m раз: Pn(m+1)+ Pn(m+2)+…+ Pn(n).
Формула Бернулли применяется, когда n — невелико (не больше 10). Если n>10, то на практике применяют: локально-интегральную теорему Муавра-Лапласа, а также формулу Пуассона.
Формула Пуассона
n- велико, порядка сотен и тысяч.
p- мало, порядка сотых и тысячных.
,
где
;
.
5.Наивероятнейшее число наступления события.
Вероятность можно рассматривать как функцию целочисленного аргумента m.
Существует
такое значение аргумента
,
при котором эта функция принимает
наибольшее значение
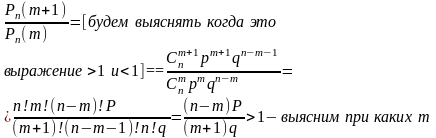np-mp>mq+q
m(q+p)<np-q, где q+p=1
m<np-q
Вывод
при таких m
при
таких m функция возростает.
И наоборот при
m>np-q
,
то есть при таких m функция убывает, то
есть действителен один
при котором функция достигает max значения
По смыслу должны выполняться два неравенства
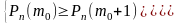
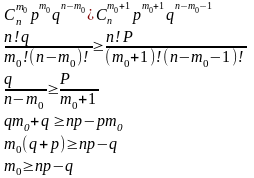
Распишем 2-е неравенство
6. Локальн теорема и интегральная теорема Муавр- 3
-Лапласа.
Локальная теорема.
Применяется, когда 0<P<1 или не слишком близко к 0 или 1.
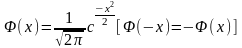
Интегральная теорема Муавра-Лапласа.
,
i=1,2,3,…
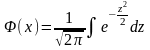- функция Лапласа
(интеграл ошибок, интеграл вероятностей)
П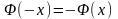
ример
300 дет. за смену
Р(1-ого сорта)=0.75 q=0.25
а) 225 штук б) от 210 до 240
а)
б)
;
;
7. Св. Функции распределения и их свойства.
СВ наз. величины к-рые могут принимать те или иные значения заранее до опыта неизвестно какие именно. Различают дискретные и непрерывные СВ.
Дискретные СВ.
Значения обознач х1,х2,…,хn,…
Всякое описание значений, к-рые может принимать СВ и соответствующие этим значениям вероятности наз. законом распределения СВ.
Для дискретной СВ:
xi |
X1 |
X2 |
… |
xn |
pi |
P1 |
P2 |
… |
pn |
;
Пример:
Вер. Того что в библиотеке нужная ему книга свободна равна 0,3. В городе 4 библиотеки. СВХ – это число библиотек к-рое посетит студент. Составить з-н распределения СВ.
xi |
1 |
2 |
3 |
4 |
Pi |
0.3 |
|
|
|
Ф-ция распределения СВ.
Ф-цией распределения или интегральной ф-цией наз. F(X)=P(X<x). Вер.того вер.Х меньше чем х:
xi |
X1 |
X2 |
… |
xn |
pi |
P1 |
P2 |
… |
pn |
Свойства:
1.
2.F(X)-функция неубывающая
X1 X2 X
Рассмотрим
событие
;
;
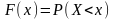-большему
значению аргумента соответствует
большее значение функции.
3.
Замечание: если случ. Величина X непрерывна то вероятность того что СВХ примет значение х равна 0.
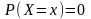ж