
- •1. Определение вероятности. 1
- •2. Условная вероятность. Независимое событие. Формула умножения вероятности.
- •4.Последовательность независимых испытаний. Схема Бернулли. Формула Пуассона.
- •Формула Пуассона
- •5.Наивероятнейшее число наступления события.
- •6. Локальн теорема и интегральная теорема Муавр- 3
- •7. Св. Функции распределения и их свойства.
- •8.Числовые хар-ки случайной величины. 4
- •9.Биномиальный закон распределения.
- •10.Распределение Пуассона. Равномерное распределение.
- •11. Показательное или экспоненциальное распределение.
- •12. Нормальный закон распределения. Числовые 6 характеристики.
- •14.Многомерные случайные величины(св)
- •15.Неравенство Маркова. Неравенство Чебышева.
- •16. Т.Чебышева. Т.Бернули. 8
- •17. Теорема Ляпунова:
- •Элементы математической статистики Генеральная выборочная совокупность
- •Повторная и бесповторная выборка
- •Репрезентативная выборка
- •Статистическое распределение выборки
- •Методы построения точечных оценок
- •Билет №1 10
- •Билет №2
- •Билет №3
- •Билет №4
- •Билет № 5
- •Билет 6.
- •Билет 7
- •Билет 8
- •Билет 9.
- •Билет 10.
- •Билет 11.
- •Билет 12.
- •Билет № 13
- •Билет 14.
- •Билет 15. 16
- •Билет 16.
- •Билет 17.
- •Билет 18.
- •Билет 19.
- •Билет 20. 18
- •Билет 27.
- •Билет 28.
- •1.Теория вероятности
- •3 Т. «Сложения вероятности несовместных событий 20
- •5Формула полной вероятности
- •6.Вероятность наступления хотя бы 1-го события
- •10Вероятность отклонения относительной частоты от постоянной вероятности
- •11Случайная величина
- •12Интегральная ф-ия распределения
- •13Дифференциальная ф-ия распределения вероятностей св (её плотность)
- •14Числовые хар-ки св
- •15Дисперсия св (дискретной)
- •16Среднеквадратическое отклонение св х –
- •17Моменты св х:
- •18Важнейшие з-ны распределения вероятностей cв:
- •21Т.Чебышева
- •22Т. Ляпунова
- •26Вероятность попадания случайной точки в полосу
- •29Числовые хар-ки 2-мерной св (с-мы св):
- •31Нормальное распределение с-мы 2-х св
Билет 27.
5) Дискретная случайная величина X задана законом распределения
x |
0,3 |
0,6 |
p |
0,2 |
0,8 |
Используя неравенство Чебышева, оценит вероятность того, что | X-M(X)|<0,2.
Неравенство Чебышева:
Найдем
мат. ожидание и дисперсию: М(Х) =
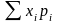 =0,3*0,2+0,6*0,8
= 0,54;
=0,3*0,2+0,6*0,8
= 0,54;
М(Х2)
=
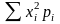 =0,09*0,2+0,36*0,8
= 0,306;D(X)
= М(Х2)–(М(Х))2
=0,306–(0,54)2=0,0144.
=0,09*0,2+0,36*0,8
= 0,306;D(X)
= М(Х2)–(М(Х))2
=0,306–(0,54)2=0,0144.
Подставим
значения:
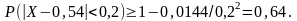 .
.
Билет 28.
5) Математическое ожидание и среднеквадратическое отклонение нормально распределенной СВ X соответственно равно 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (20,30).
М(Х)=20; σ=5; Х€(150;250). Плотность нормального распределения:
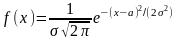 ,
где а – мат. ожидание.
,
где а – мат. ожидание.
Вероятность, что Х примет значение, принадлежащее интервалу:
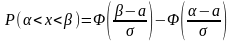 19
19
Подставим
значения: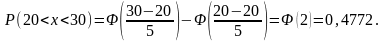
Ответ: 0,4772.
6) Случайные величины X и Y независимы. Найти дисперсию СВ z=2x+3y, Если известно, что D(x)=2, D(y)=6.
Так как и для независимых СВ , то
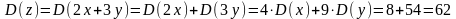
1.Теория вероятности
зависимости:
1)детерминистические (в виде мат. уравнений)
2)вероятностные
Опыт – наблюдение какого-нибудь явления, при наличии определенного комплекса условий и действий. При повторении опыта этот комплекс должен сохраняться.
Результат опыта – событие.
Явление – это событие.
События:
1)достоверное(событие, к. в р-те опыта обязательно произойдёт)
2)невозможное(при проведении опыта заведомо не произойдёт)
3)случайное(в р-те опыта м. произойти, а м. и не произойти)
Теория вероятности – матем. наука, к. занимается изучением массовых случайных явлений.
События: A,B,C,D…
Действия над случайными событиями:
1 )
A+B
)
A+B
2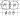 )A∙B
)A∙B
3)AB=BA
4)противопоставление (A и A¯) A+A¯=Ω
Ω – достоверное событие
A – случайное
Ø – невозможное
События:
1) несовместные – события, такие, что появление 1-го из них исключает появление 2-го.
2) совместные – не исключает
a) независимые – при проведении опыта появление одного из них не зависит от появления 2-го.
b) зависимые – зависит от появления 2-го.
I) простые (элем-ные) – события, к. не м.б. разложены на ещё более простые
1)единственно возможное – при проведении опыта м. произойти только это событие;
2) равновозможные – вероятности появления события равны;
2
Полная группа/сумма событий – события, к. при проведении опыта явл. несовместными и единственно возможными (филос.). Вероятность события – объективная возможность появления события.
Н-р, в ящике 25 деталей, из них 20 окр. и 5 неокраш. A – вынутые окраш., B – вынутые неокр.
(классич) Вероятность события A (P(A)) – отношение P(A)=m/n, где m – число благоприятных исходов испытания, n – неблагоприятных+благ-х (всевозможных).
P(A)=20/25=0,8 P(B)=5/25=0,2
(статис) N – кол-во опытов; A произошло M раз (M≤N)
M/N – относительная частота появления события
A – отношение числа событий к числу опытов.
Вероятность события – относит. частота этого события при N→∞.
Геометрическая вероятность – отношение меры одной фигуры к мере другой
P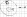 (A)=mesE/mesD
0≤P(A) ≤1
(A)=mesE/mesD
0≤P(A) ≤1
Соединение – множество любых объектов.
Н-р, (a,b,c,d)
Перестановки – такие соединения, которые отличаются только порядком. Кол-во этих перестановок равно Pn=n!
Размещения– соединения, к. отличаются др. от друга элементами или их порядком Amn=m(m-1)(m-2)…(m-(n-1)). Н-р, A42=4*3=12
Сочетания – соединения, к. отличаются друг от друга элементами
Cmn=Amn/Pn=(m!/n!(m-n)!)
Урновая схема для вычисления вероятностей
Пусть в ящике (урне) нах. N шаров, из них M красных, => (N-M) – зелёных. Из урны вынимают n шаров. Найти вероятность того, что из них m красных (событие A)
P(A)=CMm∙CN-Mn-m/CNn
Н-р, N=20, M=16, n=8, m=6
P(A)=C166∙C42/C208=
16! ∙4! ∙20!/(6! ∙10! ∙2! ∙2! ∙8!)=7∙8∙11/(5∙17∙19)
