
- •1. Определение вероятности. 1
- •2. Условная вероятность. Независимое событие. Формула умножения вероятности.
- •4.Последовательность независимых испытаний. Схема Бернулли. Формула Пуассона.
- •Формула Пуассона
- •5.Наивероятнейшее число наступления события.
- •6. Локальн теорема и интегральная теорема Муавр- 3
- •7. Св. Функции распределения и их свойства.
- •8.Числовые хар-ки случайной величины. 4
- •9.Биномиальный закон распределения.
- •10.Распределение Пуассона. Равномерное распределение.
- •11. Показательное или экспоненциальное распределение.
- •12. Нормальный закон распределения. Числовые 6 характеристики.
- •14.Многомерные случайные величины(св)
- •15.Неравенство Маркова. Неравенство Чебышева.
- •16. Т.Чебышева. Т.Бернули. 8
- •17. Теорема Ляпунова:
- •Элементы математической статистики Генеральная выборочная совокупность
- •Повторная и бесповторная выборка
- •Репрезентативная выборка
- •Статистическое распределение выборки
- •Методы построения точечных оценок
- •Билет №1 10
- •Билет №2
- •Билет №3
- •Билет №4
- •Билет № 5
- •Билет 6.
- •Билет 7
- •Билет 8
- •Билет 9.
- •Билет 10.
- •Билет 11.
- •Билет 12.
- •Билет № 13
- •Билет 14.
- •Билет 15. 16
- •Билет 16.
- •Билет 17.
- •Билет 18.
- •Билет 19.
- •Билет 20. 18
- •Билет 27.
- •Билет 28.
- •1.Теория вероятности
- •3 Т. «Сложения вероятности несовместных событий 20
- •5Формула полной вероятности
- •6.Вероятность наступления хотя бы 1-го события
- •10Вероятность отклонения относительной частоты от постоянной вероятности
- •11Случайная величина
- •12Интегральная ф-ия распределения
- •13Дифференциальная ф-ия распределения вероятностей св (её плотность)
- •14Числовые хар-ки св
- •15Дисперсия св (дискретной)
- •16Среднеквадратическое отклонение св х –
- •17Моменты св х:
- •18Важнейшие з-ны распределения вероятностей cв:
- •21Т.Чебышева
- •22Т. Ляпунова
- •26Вероятность попадания случайной точки в полосу
- •29Числовые хар-ки 2-мерной св (с-мы св):
- •31Нормальное распределение с-мы 2-х св
Билет 18.
4)Производится три независимых выстрела по мишени. Вероятности попадания в цель при 1-м, 2-м и 3-м выстрелах соответственно равны 0.6, 0.7, 0.8. СВ Х – число попаданий в цель. Найти М(х) и Д(х).
X |
0 |
1 |
2 |
3 |
P |
0.024 |
0.188 |
0.452 |
0.336 |
M(X)=2.1
D(X)= M(X2)+( M(X))2
5)В партии из 10-ти кинескопов 3 бракованных. Определить вероятность того, что из 4-х взятых кинескопов 2 будут бракованными.
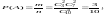
6)Найти минимальный объем выборки, при котором с надёжностью 0.975 точность оценки математического ожидания а Г.С. по выборочной средней равна δ=0.3, если σ=1.2 нормального распределения Г.С.

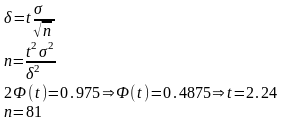
Билет 19.
4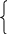 )
0 , х≤0
)
0 , х≤0
СВ задана функцией распределения F(x)= х2/9, 0<х≤3
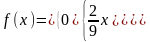
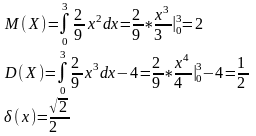
5) При установившемся технологическом процессе в среднем 0.5% шариков для шарико-подшипников оказывается бракованными. Найти вероятность того, что в партии из 1000 шариков бракованными будут 40 штук.
Вероятность
брака –0,005;По формуле Пуассона:
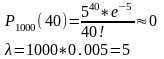
6) С помощью метода наименьших квадратов найти уравнение прямой регрессии У на Х по следующим экспериментальным данным:
-
xi
2
4
6
8
10
yi
3
3
7
9
11
Вид уравнения , Где
|
|
|
|
2 |
3 |
4 |
6 |
4 |
3 |
16 |
12 |
6 |
7 |
36 |
42 |
8 |
9 |
64 |
72 |
10 |
11 |
100 |
110 |
|
|
|
|
;
Y=1.1*X+0;Ответ: Y=1.1X
Билет 20. 18
6)Найти выборочную дисперсию по данному распределению выборки, N=50:
xi |
0,1 |
0,1 |
0,6 |
0,8 |
ni |
5 |
15 |
20 |
10 |
Перейдем к условным вариантам
Ui |
1 |
1 |
6 |
8 |
ni |
5 |
15 |
20 |
10 |
DВ (u)=(∑ni U2i)/n – ((∑ni Ui)/n )2
DВ(u) =27.6-19.36=8.24
DВ (x)= DВ (u)/102=8.24/100=0.0824
Билет 21.

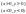

f(x,y)=
Найти M(x).
Найдем плотность распределения:
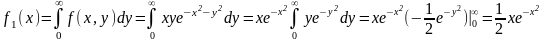
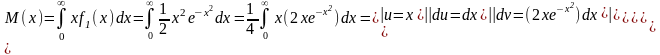
Билет 22.
6) Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 10 и 2. Найти вероятность того, что в результате испытания X примет значение заключенное в интервале (11,13).
Вероятность того, что СВ, распределённая по нормальному закону распределения, примет значение из промежутка (x1, x2) равна
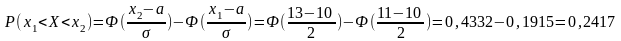
Билет 24.
4) Случайные величины X и Y независимы. Найти дисперсию СВ z=3x+2y, если известно, что D(x)=5, D(y)=7.
Так
как
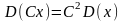 и
для независимых СВ
и
для независимых СВ
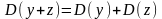 ,
то
,
то
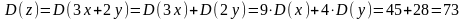
Билет 26.
5) Вероятность появления события в каждом испытании равна 1/4. Используя неравенство Чебышева, оценит вероятность того, что число X появлений события заключено в пределах от 150 до 250. если будет произведено 500 испытаний.
р=0,25; n=500; Х€(150;250). Найдем мат. ожидание и дисперсию:
М(Х) = np = 500*0,25 = 125; D(X) = npq = 500*0,25*(1–0,25) = 93,75.
Найдем максимальную разность между заданным числом появления события и М(Х):
ε =
250-125 = 125. Неравенство Чебышева:
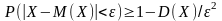
Подставим
значения: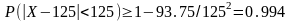 .
.
