8. О пределение криволинейного интеграла первого рода, его основные свойства и вычисление.

Кривая должна быть простой кривой, то есть .

Пусть кривая будет разбита точками разбиения. Составим интегральную сумму.

Полученный интеграл называется криволинейным интегралом первого рода.

На словах можно сказать так. Если существует предел интегральной суммы (см. выше) при стремлении к нулю наибольшей из длин Δl_k (то есть ), то этот предел называется криволинейным интегралом первого рода от функции f(x,y) по кривой L и обозначается символом или .

Если кривая задана не параметрически, а, к примеру, так: 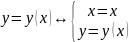, тогда .

Основные свойства:

• Линейность:

• Аддитивность (если дуга AB составлена из двух дуг AC и CB):

• Монотонность: если f<=g на L, то:

• Изменение направления обхода кривой интегрирования не влияет на знак:

• Оценка модуля интеграла:

Вычисление. Пусть L – кривая, как на рисунке, заданная параметрически. Пусть функция f(x,y) определена и интегрируема вдоль кривой l как криволинейный интеграл первого рода. Тогда: .

Таким образом, для вычисления по длине дуги АВ надо, используя параметрическое уравнение кривой, выразить подынтегральную функцию через параметр t, заменить dl дифференциалом дуги в зависимости от параметра t и проинтегрировать полученное выражение по t.

9. Определение криволинейного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.

П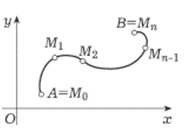 усть кривая L на координатной плоскости Оху задана параметрически уравнениями . L называется простой (плоской) незамкнутой кривой, если функции , непрерывны на и различным значениям параметра t из сегмента соответствуют различные точки , . Если точка совпадает с точкой , а остальные точки не являются кратными, то L называется простой замкнутой кривой. Простая кривая L называется спрямляемой, если существует предел (длинa кривой L) длин ломаных, вписанных в кривую, при Δt → 0.

Пусть на кривой AB заданы две функции, P(x, y) и Q(x, y). Разобьем сегмент на n частей точками . Кривая АВ разобьется на n частей точками в направлении от A к B. Пусть – координаты точки , , , – длина дуги . На каждой дуге возьмем некоторую точку (координаты ) и составим две интегральные су­ммы: , . Если существует предел интегральной суммы при стремлении к нулю наибольшей из длин , то этот предел называется криволинейным интегралом второго рода . Сумма называется общим криволинейным интегралом второго рода.

Из определения криволинейного интеграла второго рода следует, что при изменении направления обхода кривой AB изменяется и знак интеграла . Аналогично вводится для пространственной кривой, заданной параметрически

Криволинейные интегралы обладают теми же свойствами, что и обычные определенные: Линейность . Аддитивность: . Монотонность: если f g, то .

Кривая L кусочно-гладкая, если она непрерывна и распадается на конечное число не имеющих общих внутренних точек кусков, каждый из которых представляет собой гладкую кривую.

Вычисление криволинейного интеграла второго рода с помощью определенного интеграла.

Если AB – кусочно-гладкая кривая, а функции Р=Р(x,y) и Q=Q(x,y) кусочно непрерывны вдоль кривой AB, то справедливо равенство: = .

Если кривая AB задана уравнением y = у(x), a≤x≤b, и имеет кусочно-непрерывную производную, а функции P(x,y) и Q(x,y) кусочно непрерывны вдоль кривой AB, то имеет место равенство: = .

Связь между криволинейными интегралами первого и второго рода.

Пусть AB− кусочно гладкая кривая, функции Р=P(x,y) и Q=Q(x,y) кусочно непрерывны вдоль кривой AB и − единичный касательный вектор к кривой AB в точке M(x,y), причем направление соответствует направлению движения от А к В (α − угол между вектором в точке M(x, y) и осью Oх). . Для пространственной кривой справедлива аналогичная теорема: .

Из лекций:

Это и есть криволинейный интеграл второго рода.

– то же самое, только по y.

Каждый интеграл второго рода может быть сведён к первому роду.

или