28.Однородный марковский процесс. Распределение времени ожидания выхода системы из исходного состояния.

Пусть 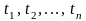- произвольные моменты времени такие, что для : имеет место:

Методом мат. индукции для можно установить равенство:

- общая ф-ла для условной вер-ти марковского однородного процесса.

Дадим характеристику этому рав-ву:

Поведение марковского процесса (не обяз. однор-го) после мом. времени , при известном сост. не зависит от его поведения в прошлом т.е до мом. времени . Выведем формулу: рассм момент времени

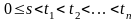. В начальный мом времени у нас задана вероятность распределения по состоянию нашего процесса: . Рассмотрим вероятность

Нашли закон совместн. распределения вер. СВ .

29. Прямая и обратная системы ду Колмогорова.

Рассм. однородный Марковский процесс с непрерывным временем, число состояний кот-го конечно, или счетно.

I. Пусть в момент времени система нах-ся в состоянии i и СВ τ есть время ожидания до ее выхода из этого состояния. Найдем ф-цию распределения и плотность СВ τ .

Предполагаем, что при условии τ >s, последующее поведение рассматриваемого однородного Марковского процесса (с точки зрения распред. СВ τ ) такое же, как и после исх. момента времени .

(*) P{τ > s+t | τ > s}=P{τ > >t}

По ф-ле для условной вер-сти имеем: P{τ > s+t | τ > s}=

Если A= { τ > s+t } и B= {τ > s} Отсюда и из рав-ва (*) вытекает то, что A=>B

P{τ > s+t}= P{τ > s} P{τ > t}

Обозн: f(t)= P{τ > t}

Тогда f(s+t)=f(s)f(t), зн. f – показат. ф-ция н-р =>

Любую показат. ф-цию можно записать с основанием e, т.е , где 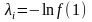(если t=1)

Заметим, что , тогда .

Т.о. Т.о.

Опр: Постоянная назыв. плотностью выхода из состояния i, если , то P{τ > t}=1, для любого t. Зн. процесс навсегда остается в состоянии i.

Находим ф-цию распределения СВ τ : t<0

Находим плотность СВ τ :

Значения в отд. взятой точке для непрерывной СВ не имеет смысла брать. Т.е. СВ τ имеет показательный (с пар-ом ) закон распределения.

II.Пусть в нач. момент времени система нах-ся в состоянии i, где пребывает случ. время с – показательным распределением вер-сти, после чего переходит в новое состояние j1 с вер-тью 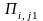(вер-сть попасть при выходе из i именно в состояние j1); в состоянии j1 система пребывает случ. время с – показат. распределение, а затем переходит в новое состояние j2 с вер-тью и.т.д.

При условии, что этот процесс продолжается во времени. Вер-ть того, что за время, не превышающее система совершит выход из исходного состояния i и попадет непосредственно (т.е. минуя пром. состояния) в состояние j равна: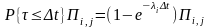

Предположим, что вер-ть более одного перехода за малое время есть . Тогда вер-ть того, что выйдя из i система ч/з окажется в состоянии 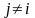будет равна:

А вер-ть того, что ч/з система не будет нах-ся в исходном состоянии i равна:

Т.о. переходные вер-ти при малом удовлетворяют усл-ям:

(1):

(2): ,

Опр: Постоянная назыв. плотностью перехода из сост. i в сост. j.

Заметим, что

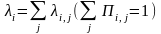
{в силу ур-я Колмагорова - Чепмена}

Т.о.

Поделим обе части на :

;

; ;

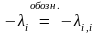Перейдем к

т.к. i,j = 1,2,…

Получим систему, кот-ая наз. обратной системой ДУ Колмогорова. Если бы мы исп. правую часть исх. рав-ва, стоящую в скобках, то получили бы систему:

– прямая система ДУ Колмогорова.

Добавим нач. усл-я: по смыслу ( )

Примечания: Осуществленный выше формально пред. переход при имеет место при усл-ии, что ф-ции дифференцируемы и число состояний системы конечно.

Приведем без д-ва указ. пред. перехода соотв. теоремы для случая числа состояний.

Теорема: Пусть переходные вер-ти диффер. ф-ции. Пусть выполнено усл-е (1), (2), тогда имеет место обратная система ДУ Колмогорова.

Теорема2: Пусть – дифф. ф-ции; пусть вып-но (1) и (2); пусть плотности перехода равномерно по i ограниченны для каждого j (т.е. ) и в выр-ях (1), (2)

равномерно по всем i ( : => )

Тогда имеет место прямая система ДУ Колмогорова.