1. Стохастическая зависимость. Регрессионная зависимость. Эмпирическая функция регрессии.

Стохастическая зависимость.

Пусть некоторая переменная описывается двумерным случайным вектором (x,y). Ставится вопрос о 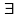зависимости между компонентами этого вектора, т.е. случайными величинами (признаками X и Y). Изучаются форма и сила (теснота) связи между ними.

Различают два вида зависимостей: функциональную и стохастическую (вероятностную). Функциональная зависимость это однозначное отображение множества С.В. Х в множество С.В. Y.

Стохастическая зависимость означает, что изменение одной С.В. влечёт за собой изменение закона распределения другой С.В. Однако точно определить значение второй С.В. по значению первой нельзя.

Пример: Если Х зависит от случайных факторов z₁, z₂, v₁, v₂, а Y от z₁, z₂, u то между Y и X имеется стохастическая зависимость, т.к. среди случайных факторов есть общее z₁, z₂.

Регрессионная зависимость.

В частности стох-ая зависимость проявляется в том, что при изменении одной из величин изменяется мат. ожид другой. Т.е. условное мат. ожидание: M {Y| X=x} = (x).

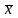Условное мат. ожидание является функцией от х. И наоборот: M {X| Y=y} = (y).

Зависимости такого рода называются регрессионными. Функции (x) и (y) называются функциями регрессии соответственно Y на Х и X на Y. Графики функций (x) и (y) называются линиями регрессии Y на Х и X на Y. Ставятся две основные задачи:

1. Установить форму связи между С.В. X и Y. Т.е. вид функции регрессии.

2. Оценить тесноту или силу связи.

Теснота зависимости Y от Х оценивается по величине расстояния значений С.В. Y вокруг условного мат. ожидания (x). Для данного значения Х=х будем наблюдать рассеяние значения Y около центра (x). Мерой этого рассеяния служит условная дисперсия С.В. Y при данном фиксированном Х.

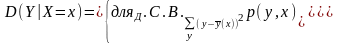В первом p это вероятность, а во втором плотность.

Величину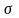 (Y|X=x)= 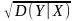можем рассматривать как среднюю квадратичную погрешность прогноза С.В. Y по наблюдённому значению х С.В. Х, если использовать для прогнозирования известную функцию регрессии (x).

Величина (Y|X) и следовательно точность прогноза С.В. Y зависит от х. Для представления о точности прогноза Y по всем наблюдённым значениям х мы должны взять средне взвешенное по вероятности из условных дисперсий.

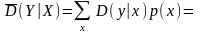
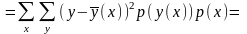
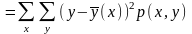
Регрессия (x) является функцией минимизирующей среднюю квадратичную погрешность прогноза Y по Х, т.к. рассеяние измеряемое средним квадратом отклонения значений y около центра рассеяния (x) при каждом х - минимально.

M(Y-b)²=M((Y- (x))+( (x)-b))² =M(Y- (x))²+2M(Y- (x))( (x)-b) +( (x)-b)² M(Y- (x))²

Эмпирическая функция регрессии

Для нахождения функции регрессии (x) или (y) надо знать закон распределения С.В. (X,Y). Однако на практике этот закон, как правило, не известен. Поэтому, исходя из экспериментальных данных, строят оценку функции регрессии.

Пусть в результате наблюдения над двумерной С.В. X,Y получена выборка (x_i, y_i), где i=1..n. Оценкой функции регрессии (x) служит эмпирическая функция регрессии Y на Х. 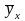=f(x, a₀, a₁, a₂, …,a_m)

Вид функции регрессии и её оценки выбирают из анализа расположения точек (x_i,y_i) на корреляционном поле. Корреляционное поле это изображение наблюдённых данных в виде точек ДПСК. Эмпирическая функция регрессии =f(x,a₀,a₁,a₂,…,a_m) должна удовлетворять условию S(a₀,a₁,a₂,…,a_m)=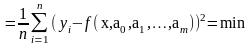

Т.е. значение параметров a₀,a₁,a₂,…,a_m должно быть выбрано так, чтобы значение f(x,a₀,a₁)=a₁x+a₀ Если среди наблюдённых значений есть одинаковые, то имеем равенства: S(a₀,a₁,a₂,…,a_m)=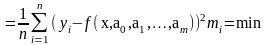 , где m_i- частота пары значений (x_i, y_i).

Т.о. для определения параметров a₀,…,a_m применяется метод наименьших квадратов.

Этот метод позволяет при заданном виде эмпирической функции регрессии так найти неизвестные параметры, что функция =f(x, a₀, a₁, a₂, …,a_m) будет наилучшей оценкой функции регрессии (x) в том смысле, что сумма квадратов отклонений наблюдённых значений С.В. Y от соответствующих ординат эмпирической регрессии будет минимальной. Аналогично определяется эмпирическая функция регрессии X на Y.

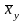=g(y, b₀, b₁, b₂, …,b_k)