16.Дифференцируемость случайного процесса в среднем квадратичном

Пусть СП определен на инт. . Пусть --фикс. кочка. --бегающая. .

Опр. производной СП в точке наз. СП , определяемый равенством

для диф-ти СП на инт. необх. и дост., чтобы его мат. ожидание 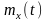было дифф. ф-ией на кореляц. ф-ия имела вторую смеша-нную производную на диагонали .

Для мат. ож. к дисперсии, и кореляц. ф-ии СП имеет место формула

корреляционная ф-ия

17.Интегрируемость случайного процесса в среднем квадратичном

Пусть СП определен на инт. .

Опр. Интегралом СП на наз. случ. вел. :

,

где

Если верхний предел интегрирования переменный, то результатом интегрирования будет СП, аргументом которого является этот перем. предел, т.е.

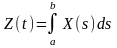,где

имеют место следующие формулы:

,

.

18.Винеровский процесс как математическая модель процесса броуновского движения.

Рассм. частицу, испытывающую хаотические столкновения с молекулами жидкости. В результате она находится в непрерывном беспорядочном движении, называемом Броуновским.

Рассм. одномерное Броуновское движение. Считаем это движение дискретным сначала, а именно положение частицы рассм-ся только в дискретные моменты времени:

кратные

Находясь в точке x, частица независимо от предшествующего поведения переходит с равными вероятностями в одну из соседних точек: или

причем смещение одно из точек для любых точек х. В пределе, когда определенным образом получается непрерывное, случайное блуждание.

Обозначим ч/з положение частицы в момент времени t. Пусть .При дискретном блуждании за время t она совершает шагов. Обозначим ч/з смещение частицы на к-ом шаге, т.е. - это СВ с равными вероятностями . Тогда СП можно представить в виде: ,где -независимо одинаково распр-мые СВ. Рассм. положение частицы в момент времени 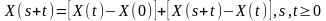s и t –кратны .

Очевидно, что в расс-нной модели: и

эти СВ независимы, причем распре-деление вероятностей СВ такое же как распр. вер-ей СВ . Далее

будем предполагать, что этими св-ами бладает и непрер. модель процесса Броуновского движения .

В

₁₈-2

силу этих свойств имеем:

т.е. функция как ф-ия от t явл. лин. однородной ф-ией

, ( )

где --некоторая положительная постоянная, наз. коофф. диффузии.

С учетом найденной дисперсии пред-ставим поведение частицы с течением времени:

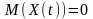
с другой стороны

сравнивая эту формулу с ( ) получаем. 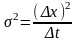. В дальнейшем устремляя отношение будем считать постоянным. Рассм. предел .Далее восп-мся централ. предельной. Будем ее применять для СВ:

₁₈-3

В дальнейшем будет предель-ная СВ

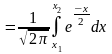
и --их распределение одинаково.

В связи с этим можем сделать вывод, что справедливо и для приращения ф-ий. Т.О. при мы получим семейство СВ , где , таких что:

1)

2) приращение , где имеют нормальные распределения вер-ей с мат. ожид. =0 и дисп. =

3)для любых не пересекающихся инт-ов. , приращ. незав-ые СВ.

Опр.СП обладающий св-ами 1)-3) наз. Винеровским процессом.

В случае если его называют также стандартным винеровским процессом.

Св-ва станд-ого Вин-ого процесса:

Рассм. след. СВ: величина максимального смещения вправо частицы n . --момент времени, в кот. траектория достигает в первый раз точки а. (каждому t соответствует одно х.)