
- •1. Стохастическая зависимость. Регрессионная зависимость. Эмпирическая функция регрессии.
- •2. Линейная регрессия.
- •3. Статистический коэффициент корреляции
- •5. Статистический коэффициент корреляции. Условие отсутствия линейной корреляционной связи между св.
- •6. Критерий существования линейной функциональной связи между св
- •7. Критерий совпадения линий регрессии y на X и X на y.
- •8. Статистический коэффициент корреляции как мера тесноты линейной корреляционной связи между случайными величинами.
- •9. Статистическое корреляционное отношение. Оценка статистического корреляционного отношения.
- •10.Условие отсутствия корреляционной связи между св. Функциональная зависимость св.
- •11.Корреляционное отношение как мера тесноты корреляционной связи между св.
- •12.Определение случайного процесса (сп). Законы распределения случайных процессов.
- •13.Основные характеристики случайных процессов
- •14.Классификация случайных процессов.
- •15. Непрерывность случайных процессов.
- •16.Дифференцируемость случайного процесса в среднем квадратичном
- •17.Интегрируемость случайного процесса в среднем квадратичном
- •18.Винеровский процесс как математическая модель процесса броуновского движения.
- •19.Винеровский процесс как математическая модель процесса броуновского движения.
- •21. Пуассоновский процесс, его одномерный закон распределения.
- •22.Свойства однородности и отсутствия последствий Пуассоновского процесса(пп).
- •24.Марковский процесс и его свойства.
- •25.Уравнение Колмогорова- Чемпена.
- •26.27. Коэф-т эргодичности. Эргодическая теорема для однородного Марковского процесса.
- •28.Однородный марковский процесс. Распределение времени ожидания выхода системы из исходного состояния.
- •29. Прямая и обратная системы ду Колмогорова.
- •30. Ветвящиеся процессы. Производящие функции.
- •31.Ветвящиеся процессы. Дифф уравнение для производящей функции.
- •32.33.34 Анализ ду для производящей функции ветвящегося процесса. Стремление к стационарному состоянию. Исследование вопроса о числе интегральных кривых, проходящих через точку (0,1).
- •35.Эффекты вырождения и взрыва ветвящегося процесса
- •36, 37 Каноническое разложение случайного процесса
- •38.Спектральное разложение стационарного случайного процесса
30. Ветвящиеся процессы. Производящие функции.
Имеется совокупность частиц, которые с течением времени превращаются в частицы такого же типа или исчезают.
При этом каждая из исходных частиц за промежуток времени t независимо от др. ч-ц и от обстоятельств, предшествовавших исходному моменту, и одинаков. для всех част-ц вер-стью pn(t) переходит в группу из n ч-ц.
Введём обозначения:
пусть X(t) – число ч-ц, имеющихся в момент времени t.
Очевидно, что эволюция вел-ны X(t) представляет собой однородный Марковский пр-сс. Будем называть его ветвящимся.
Пусть в исх. момент времени t0=0 имеетя k ч-ц:
Xi(t) – число имеющихся в момент времени t ч-ц, порождённых i-той ч-цей.
Тогда: X(t)=X1(t)+ X2(t)+…+ Xk(t), t=1,2,…,k.
Случ. в-ны Xi(t), где i = 1,2,…,k независимы и имеют одно и то же распределение вероятностей: P(Xi(t)=n) = pn(t).
Предположим, что отдельн. ч-ца за мал. пром-к времени Δt с вер-ю pn(Δt) = λnΔt + Ỗ(Δt), при n≠1 превращается в n новых ч-ц (или исчезают при n=0), а с вер-ю p1(Δt) = 1 – λ(Δt) + Ỗ(Δt) остаётся неизменной.
λn≥0, λ≥0.
Обозначения: λ1 = - λ , Σi λi=0 .
Будем предполагать, что переходные вероятности pkn(t) удовл-т обратной сис-ме ДУ Колмогорова:
p1n`(t) = Σk=0∞ λk pkn(t) (*), n=0,1,2,…
pkn(t) - вер-сть того, что k ч-ц за время t переходят в n ч-ц.
Введём следующие ф-ции:
F(t,z) = Σn=0∞ pin(t)zn - поколение одной ч-цы,
Fk(t,z) = Σm=0∞ pkn(t)zn k=0,1,2,… - поколение k ч-ц
Эти ф-ции наз-ся производящими (ф-циями данного ветвящегося пр-сса).
Отметим, что ряды, опред-ие ф-ции F(t,z) и Fk(t,z), сход-ся при |z≤1|, z€C.
[Ряды Σn=0∞|pin(t)zn| и Σm=0∞|pkn(t)zn| сход-ся, потому и ряды выше сх-ся абсолютно.]
31.Ветвящиеся процессы. Дифф уравнение для производящей функции.
Имеется
совокупность частиц, которые с течением
времени превращаются в частицы такого
же типа или исчезают. При этом
из
исходных частиц за промежуток времени
t
независимо от других частиц и от
обстоятельств, предшествовавших
исходному моменту, с одинаковой для
всех частиц вероятностью
 переходят в группу из n
частиц. Пусть X(t)
– число частиц, имеющихся в момент
времени t.
Очевидно, что эволюция величины X(t)
представляет собой однородный Марковский
процесс. Будем называть его ветвящимся.
переходят в группу из n
частиц. Пусть X(t)
– число частиц, имеющихся в момент
времени t.
Очевидно, что эволюция величины X(t)
представляет собой однородный Марковский
процесс. Будем называть его ветвящимся.
Пусть
в исходный момент времени
имеется k
частиц. Обозначим через
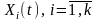 независимы и имеют одно и тоже распределение
вероятностей:
независимы и имеют одно и тоже распределение
вероятностей:
 ,
n=0,1,2,…
,
n=0,1,2,…
Очевидно,
что
 .
.
Предположим,
что отдельная частица за малый промежуток
времени
с вер-ю
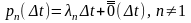 превращается в n
новых частиц (или исчезают в случае
превращается в n
новых частиц (или исчезают в случае
 ),
а с вероятностью
),
а с вероятностью
 остается
неизменной. Обозначим
остается
неизменной. Обозначим
 .
.
 -предположение.
-предположение.
 ,
,
 -
сходится абсолютно.
-
сходится абсолютно.
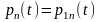 -
удовлетворяет ДУ Колмогорова:
-
удовлетворяет ДУ Колмогорова:
 [1],
где
[1],
где
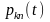 -
вероятность того, что k
частиц за время t
переходят в n
частиц. Введем производящие
функции:
-
вероятность того, что k
частиц за время t
переходят в n
частиц. Введем производящие
функции: ,t-параметр
,t-параметр
z-
комплексная переменная,

Свойства производящих функций:
1.Ряды
определяющие ф-ции
 и
и
 сходятся при
сходятся при
 .
2.
В силу [1] имеем, что все
.
2.
В силу [1] имеем, что все
 (равномерно
по n
ограничены и const
единств для всех n).
(равномерно
по n
ограничены и const
единств для всех n).
 -сходится
-сходится
=>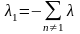 -
сходится к
-
сходится к

 а
наш ряд отличается лишь одним слагаемым
|
|,
во всех остальных модуль можно убрать.
а
наш ряд отличается лишь одним слагаемым
|
|,
во всех остальных модуль можно убрать.
Зн.
при
 ряд
ряд
 будет сходится равном, но по
.
будет сходится равном, но по
.
 ,
,
 .
Далее воспользуемся т.Вейерштрасса:
.
Далее воспользуемся т.Вейерштрасса:
 -
сходится при
.
-
наш ряд сх равномерно. Поэтому ряд
-
сходится при
.
-
наш ряд сх равномерно. Поэтому ряд
 можно
почленно продифф-ть по t.
Дифф-ем и используем [1]:
можно
почленно продифф-ть по t.
Дифф-ем и используем [1]:
 Т.о.
Т.о.
 [2]
[2]
 ,
,
 .
Т.к.
.
Т.к.
 ,
,
 -
независимые СВ =>
-
независимые СВ =>

 Посчитаем
при
Посчитаем
при
 ,
т.е.
,
т.е.
 -
справедливо.
-
справедливо.
Равенство
[2] можно переписать в виде:
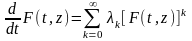 [3]
[3]
Будем считать, что заданными параметрами ветвящегося
Процесса
явл. плотность перехода, т.е
 Введем в рассмотрение ф-цию
Введем в рассмотрение ф-цию

Функция f(x) является аналитической при -1<x<1, т.к ряд инт-м. В силу [3] F(t,z) явл-ся решением ДУ:

Определимся с нач условиями:

Т.о
F(t,z)
–решение указанного ур-я, удовлетворяет
нач. условию

