32.33.34 Анализ ду для производящей функции ветвящегося процесса. Стремление к стационарному состоянию. Исследование вопроса о числе интегральных кривых, проходящих через точку (0,1).

Рассмотрим . Внутри [0;1) функция является аналитической. Заметим, что при х=1 ряд, сходится. По теор. Абеля ряд сходится равномерно на [0;1] => S(x) – сумма ряда явл. функцией непрерывной на [0;1] => непрерывна слева в х=1 => f(x) – непрерывна на [0;1].

В точке х=1 функция f(x) может не иметь конечной производной.

Найдем 2-ую производную от функции f(x): =>

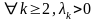
1) если при на (0;1), зн-т f(x) – выпукла вниз на (0;1).

2) если при , зн-т на инт-ле (0;1) ф-ия f(x) будет линейной, т.е. , где .

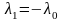Отметим характерные точки f(x). Зн-ие х=1 явл. корнем ур-я f(x)=0[т.к. =0].

В силу св-в ф-ии f(x) это ур-ие f(x)=0 может иметь еще один корень .

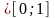Если этим корнем явл. х=0.

Если .

Предположим - наим. корень ур-я f(x)=0 на отр. [0;1] => - инт. кривая ДУ .

Пусть

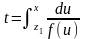Рассмотрим интегральную кривую: Рассмотрим как ведет себя t(x) при

, если ;

, если

!!!

=> наш интеграл расходится

Из вышесказанного => x(t) строго возрастает при . В силу теоремы Вейерштрасса конечный предел:

Можно показать, что предельное зн-ие явл. корнем ур-я f(x)=0. Т.к. - наим. корень ур-ия f(x)=0 на [0;1]=> .

Аналогично при можно рассм. инт. кривую, проходящую через точку . x(t) – строго убывает при , ,

Если , исследуем вопрос о числе инт. кривых, проходящих через точку t=0, x=1:

1) Допустим,

Этот ин-л расходится, когда

Тогда

Интегральная кривая примет вид: для точки ур-ние.

Найдется такое, что - это наше время, => инт. кривая в момент времени t=0 находится в точке z => инт. кривая пересекает в точке (0,z) => x(t)=1 – единственная инт. кривая, проходящая через (0,z).

2) Допустим, что интеграл , т.е. сходится. Тогда при большом может случиться, что . Выйдет на инт. кривую x=1 в какой-то момент времени 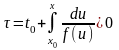=> через (0;1) проходит семейство инт. кривых , каждое из которых отвечает своему , где - момент выхода инт. кривой на x=1, если идти в обратную сторону.

Легко видеть, что , где x(0,z)=z. Т.е. - предельная для других инт. кривых x(t,z) лежащих ниже ее. случиться, что ерез ()т вид зн-ие явл.

35.Эффекты вырождения и взрыва ветвящегося процесса

Если для некоторого ветвящегося процесса λ₀=0, то имеется положительная вероятность того, что через некоторое время t не останется ни одной частицы. Если в исходный момент времени имелась одна частица, то

p₀(t)=F(t,0) , где F(t,0) – интегральная кривая, выходящая из начала координат.

p₀(t) – решение дифференциального уравнения x’=f(x), x(0)=0

p_k0(t)=F_k(t,0)=[F(t,0)]^k=[p_k(t)]^k

В силу доказанного, имеем, что p₀(t)α при t∞.

Предельное значение p₀=α называется вероятностью вырождения.

Если 0≤х<1, f(x)>0 следовательно, α=1.

Рассмотрим явление взрыва. Вероятность того, что взрыв произойдёт до момента времени t, если была одна частица, получится:

p_∞(1)=1-P{X(t)<∞}=1- ∑^∞ _n=0P{X(t)=n}=

=1-∑^∞ _n=0p_k(t)=1- lim_{z 1-0} F(t,z)

Когда x(t)≡0, то единственная интегральная кривая проходит через точку (0;1).

Имеем: Т. о., если ,

,

то p_∞(t)=0 – возможность взрыва исключена. Если интеграл сходится, то

Т о, p_∞(t)=l-x₀(t)- вероятность вырождения p_∞(t)>0 для t>0.