22.Свойства однородности и отсутствия последствий Пуассоновского процесса(пп).
Однородность.
Покажем,
что ПП является однородным , а именно
При фиксированном
не
зависит от
.
Пусть
X(t)-
ПП с данным параметром
.Пусть
и
фиксировано. Рассмотрим новый случайный
процесс:
,
Докажем, что это случайный ПП с тем же параметром .
1)
2)
,
интервалы
и
не
пересекаются.
Т.к.
интервалы
и
не
пересекаются, то не будут пересекаться
и интервалы
и
.
X(t)-процесс
с независимыми приращениями, то
тоже
будет независимая случайная величина.
Т.о.
процесс
с независимыми приращениями.
3)Очевидно, что в случайный момент времени получает приращения =1.Т.к. таким свойством обладает случайный процесс X(t).
Кроме
того рассмотрим
или
Т.о.
-это
ПП с тем же, что и X(t)
параметром
.А
поэтому распределение вероятности:
Этим в силу произвольности доказана однородность случайного процесса X(t).
Отсутствие
последствий.
и
В силу независимости приращений имеем:
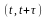и
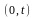не
пересекаются.
Случайный процесс обладающий таким свойством называется процессом беспоследствия
23. Закон распределения интервала времени между последовательными скачками Пуассоновского процесса.
Пусть -СВ равная длине интервала времени между 2-мя последовательными скачками Пуассоновского процесса Х(t) с параметром .
Пусть
предыдущий скачок произошел в момент
времени t0
Находим
функцию распределения величины :
Т.е. СВ имеет распределительный с параметром закон распределения.
24.Марковский процесс и его свойства.
Рассмотрим
семейство целочисленных СВ X(t),
-время.
Значение X(t)
–это возможное состояние некоторой
системы. Эти состояния нумеруются (0-е,
1-ое, 2-ое, …). Обознач: i,j,
.
Т.о. величины X(t)
описывает
случайный процесс (СП) переходов из
одного состояния в другое.
Свойства:
Предполагаем,
что для
где n-любое,
таких что
выполняется равенство:
-
произвольные состоян. процесса X(t).
Это
свойство называется свойством Марковости.
Предполагаем, что для
таких, что
и для
возможных
состояний процесса: i,j
имеет место:
т.е.
указанная условная вероятность не
зависит от расположения мом. времени
на временной оси, а зависит лишь от
разности между этими моментами:
-
функция от
.
Это св-во наз. св-ом однородности.
Опр.
СП указанного вида обладает св-ми
Марковости, однородности и назыв.
однородным марковским процессом со
счетным числом состоянии. СП обладающий
св-ом Марковости наз-ся Марковским,
однако мы будем рассм. именно однородные
марковские процессы. Опр.
Условная вер.
наз.
переходной вер-ю.(вер. перехода из
состояния
в состояние
).
25.Уравнение Колмогорова- Чемпена.
Теорема: Переходные вероятности однор. марк. процесса X(t) , удовлетвор рав-ву:
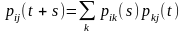
Доказательство.
Выпишем
одно слагаемое прав. части формулы:
Просуммируем по всем k обе части этого рав-ва:
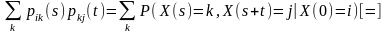
Т.е
у нас есть
;
Ч.т.д.
26.27. Коэф-т эргодичности. Эргодическая теорема для однородного Марковского процесса.
Эргодичность – из теории динамических систем означает св-во таких систем, что при некот, усл-ях состояния системы эволюционирующих во времени нах-ся близко к своим состояниям. (св-во динамических систем)
Рассмотрим однородный Марковский процесс с бесконечным, или конечным числом состояний.
Опр:
Величина
наз-ся коэф. эргодичности.
Замечание:
Коэф. эргодичности удовлетворяет:
Д-во:
и
=>
=>
=>
Ч.т.д.
Теорема:
Если k(τ)>0,
τ>0, то существуют пределы
,
j=1,2...
(кроме
существования этих пределов в ф-ле есть:
предельные вер-сти
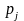не зависят от начального состояния i)
Д-во:
Зафиксируем произв.
и произв. состояние. Для произв. пары t,
j
определим 2 величины: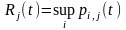
- это конечная величина не превосходящая
1.
Справедливо: (*)
,
Возьмем
произв. момент времени
,
i-
произв. состояние процесса.
{Исп. т. Вейерштрасса: достаточное усл-е существования предела монотонной огр-ой ф-ции}
Рассм.
(**)
{Согласно
Ур-ию Колмогорова - Чепмена}
Рассм.
(хотим п-ть, что
и
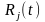имеют конечный предел при
)
,
где
Из
последней строчки и рав-ва (**)
вытекает:
Из
этого нер-ва следует
Отсюда следует, что – не убывает, при добавлении s, может только возрасти.
Аналогично - не возрастает. – ограниченно сверху и возрастает
– ограниченно снизу и убывает
Установили
выполнение условий теоремы Вейерштрасса,
следовательно,
и
Док-м, что эти пределы равны:
Рассм.
след. разность: τ
– из условия
Х
– мн-во, причем
.
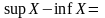
Используем ур-е Колмогорова - Чепмена:
={разбиваем
сумму под знаком sup
на 2 суммы, и это разбиение – при произв.
фиксир.
и
}= {ч/з
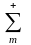и
обозн. суммы, для кот-ых разность
‘+’ и ‘-’ соответственно}=
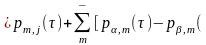
Имеет
место:
,
где
.
Тогда
П-жем, что
и
отличаются
только знаком:
,
где
и
То
есть
.
Т.о.
{d=1-k(t);
k(t)>0;
}=
{нами д-но:
}
Рассм
.
{исп.
выведенное нер-во n
раз}
Теперь
.
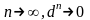
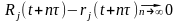Мы
установили ранее, что существуют пределы,
а из последнего следует, что эти пределы
совпадают:
Обозн.
значение предела:
;
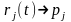Ч.т.д.