19.Винеровский процесс как математическая модель процесса броуновского движения.
Очевидно,
что
и
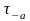имеют
одинаковые распределения вер-ей. т.к.
,
а и-а симм. относ. 0 и частица b
дискретной модели дви-жется вправо и
влево с одинак. веро-ятностями. поэтому
будем считать в дальнейшем a>0.Найдем
след. вер-сть:
.
Рассм. след. вер. :
Рассм.
событие :
Из
.Если
исп. операции над мн-ами., то
.
если
рассм. круги Эйлера. Из всего этого видно
(
)
Условная
вероятность
равна веро-ятности того что после выхода
и т. а в некот. момент вр. t
нах-ся правее точки а [вероятность
нахождения в т. а в мом. вр.
].
Из соображения симм-ти вытекает, что
эта вер-сть ок-ся в этом момент вр. левее
т. а
Из
(
)
и
.
Отсюда
,
что ф-ия распределения:
,
при
.
Т.к.
t-время,
нач-щееся с нуля. Найдем плотность
распределения СВ
.
Рассм.
Отметим еще одно св-во:
=
для любой т. а величина конечна с вероятностью 1. Это означает, что броуновская частица рано или поздно (в некот. случ. момент вр.) попадает в люб. т. а.
20.Распределение случайной величины Yt = max X(s) (0≤s≤t) для стандартного винеровского процесса.
Рассмотрим
2 СВ:
-величина
максимального смещения вправо броуновской
частицы и
-момент
времени, в который траектория X(t)
достигает впервый раз точки а.
Каждому t соответствует одно х.
Распределение
вероятностей
.
Очевидно, что
и
имеют
одинаковые распределения вероятностей.
Т.к. Х(0)=0, а и –а симметричны относительно
0 и частица в дискретной модели движется
в право и влево с одинаковой вероятностью.
Поэтому будем считать в дальнейшем a>0.
Найдем следующую вероятность: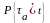
.
Для
этого рассмотрим следующую вероятность(*):
Условная
вероятность
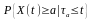равна
вероятности того, что после выхода из
точки а в некоторый момент времени
предшествующий t,
частица в момент времени t
находится правее точки а (вероятность
нахождения в точке а в момент времени
t=0)
(**)
Из (*) и (**) следует:
Отсюда
следует, что функция распределения:
при t>0.
приt<0.
Т.к. t время начинающееся с нуля.
Найдем
плотность распределения СВ
.Найдем
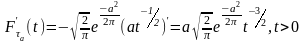и
.
Отметим еще одно свойство, найдем вероятность события:
Для
любой точки а величина
конечна с вероятностью 1. Это означает,
что броуновская частица в некоторый
случайный момент времени попадает в
любую точку а.
Рассмотрим СВ
Пусть x>0.Рассмотрим 2 события:
и
Максимальное
отклонение от начала координат за время
.
Пусть
произойдет событие А, тогда верно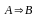
.Верно
и обратное
.
Значит
.Следовательно,
вероятности этих событий одинаковы:
Найдем функцию распределения и плотность распределения:
при
x>0
при x<0.
Отметим следующий факт
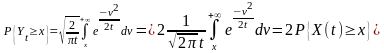
СВ имеет удвоенный нормальный закон распределения вероятностей.
Отметим следующий факт
Можно
рассматривать
Т.о.
эти 2 равенства означают , что броуновская
частица за любое сколь угодно малое
время t>0
побывает как правее исходной точки
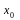так
и левее ее.
21. Пуассоновский процесс, его одномерный закон распределения.
Случайный
процесс X(t),
где
называется
Пуассоновским, если он удовлетворяет
следующим свойствам:
1)Х(0)=0;
2) X(t) процесс с независимыми приращениями;
3)В
случайный момент времени происходят
приращения значения X(t)на
единицу времени, причем для любого
момента времени
имеет
место следующее равенство:
,
,
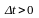интенсивность.
,
,
.
К ПП относятся:
-процесс радиоактивного распада, где X(t)-число атомов распавшихся за время е;
-поток заявок на АТС, где X(t)-число вызовов за время е;
-сбои аппаратуры, где X(t)-число сбоев за время t, и т.д.
Рисунок
Найдем
одномерный закон распределения ПП X(t).
Введем обозначения:
,n=0,1,…
Задача
состоит в отыскании вероятности
.Рассмотрим
событие
Это событие представим в виде следующей суммы событий
При
n=0:
Слагаемые
в правой части –это несовместные
события. А случайные величины
и
-независимые,
т.к. интервалы времени
и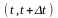
не пересекаются.
X(t) -процесс с независимыми приращениями. Поэтому получаем
Отсюда
и из свойства 3) определения ПП следует:
(*)
Для
n=0
имеем:
(**)
Теперь будем работать с (*) и (**):
Для
n=0
имеем
Делим
обе части этих равенств на
и переходим к пределу при
:
и
,
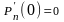при n>1
Решая
данное дифференциальное уравнение с
начальными условиями , получаем:
