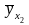- •1. Стохастическая зависимость. Регрессионная зависимость. Эмпирическая функция регрессии.
- •2. Линейная регрессия.
- •3. Статистический коэффициент корреляции
- •5. Статистический коэффициент корреляции. Условие отсутствия линейной корреляционной связи между св.
- •6. Критерий существования линейной функциональной связи между св
- •7. Критерий совпадения линий регрессии y на X и X на y.
- •8. Статистический коэффициент корреляции как мера тесноты линейной корреляционной связи между случайными величинами.
- •9. Статистическое корреляционное отношение. Оценка статистического корреляционного отношения.
- •10.Условие отсутствия корреляционной связи между св. Функциональная зависимость св.
- •11.Корреляционное отношение как мера тесноты корреляционной связи между св.
- •12.Определение случайного процесса (сп). Законы распределения случайных процессов.
- •13.Основные характеристики случайных процессов
- •14.Классификация случайных процессов.
- •15. Непрерывность случайных процессов.
- •16.Дифференцируемость случайного процесса в среднем квадратичном
- •17.Интегрируемость случайного процесса в среднем квадратичном
- •18.Винеровский процесс как математическая модель процесса броуновского движения.
- •19.Винеровский процесс как математическая модель процесса броуновского движения.
- •21. Пуассоновский процесс, его одномерный закон распределения.
- •22.Свойства однородности и отсутствия последствий Пуассоновского процесса(пп).
- •24.Марковский процесс и его свойства.
- •25.Уравнение Колмогорова- Чемпена.
- •26.27. Коэф-т эргодичности. Эргодическая теорема для однородного Марковского процесса.
- •28.Однородный марковский процесс. Распределение времени ожидания выхода системы из исходного состояния.
- •29. Прямая и обратная системы ду Колмогорова.
- •30. Ветвящиеся процессы. Производящие функции.
- •31.Ветвящиеся процессы. Дифф уравнение для производящей функции.
- •32.33.34 Анализ ду для производящей функции ветвящегося процесса. Стремление к стационарному состоянию. Исследование вопроса о числе интегральных кривых, проходящих через точку (0,1).
- •35.Эффекты вырождения и взрыва ветвящегося процесса
- •36, 37 Каноническое разложение случайного процесса
- •38.Спектральное разложение стационарного случайного процесса
7. Критерий совпадения линий регрессии y на X и X на y.
 -
статистический
коэфф-т корреляции
-
статистический
коэфф-т корреляции
 -
статистическая
ковариация
-
статистическая
ковариация
 -
статистические
среднеквадратичные отклонения
-
статистические
среднеквадратичные отклонения
Теорема:
 тогда
и только тогда, когда линии регрессии
У на Х и Х на У совпадают.
тогда
и только тогда, когда линии регрессии
У на Х и Х на У совпадают.
Доказательство:
(=>)
 //линия
регр-и У на Х
//линия
регр-и У на Х

Обе
прямые проходят через одну точку
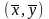
Угловые
коэффициенты:
 ,
,

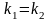 ,
значит одна прямая.
,
значит одна прямая.
(<=)
Если одна прямая, должно выполняться :


ЧТД.
8. Статистический коэффициент корреляции как мера тесноты линейной корреляционной связи между случайными величинами.
Выясним смысл коэф-та линейной корреляции :


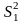 -
сумма
квадратов отклонений экспериментальных
данных от линии регрессии по ординате,
рассеяние эксперимент-х данных вокруг
линии регрессии.
-
сумма
квадратов отклонений экспериментальных
данных от линии регрессии по ординате,
рассеяние эксперимент-х данных вокруг
линии регрессии.
Если
 ,
то
сила линейной корреляционной связи
между величинами растет, точки
экспериментальных данных все ближе к
линии регрессии.
,
то
сила линейной корреляционной связи
между величинами растет, точки
экспериментальных данных все ближе к
линии регрессии.
Если
 ,
то лин-я корр-я связь м-ду Х и У уменьшается.
,
то лин-я корр-я связь м-ду Х и У уменьшается.
ВЫВОД: статистический коэфф-т корр-и является мерой тесноты линейной корреляционной связи между Х и У.
9. Статистическое корреляционное отношение. Оценка статистического корреляционного отношения.
Будем исследовать тесноту любой (нелинейной) корр-й связи м-ду случайными величинами Х и У.
x\y |
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ;
=
;
= ;
;

Для каждого xi найдем значение у


X |
x1 |
x2 |
|
xk |
|
|
|
|
|
ni |
n1 |
n2 |
|
nk |
Величины
 называют
групповыми условными средними.
называют
групповыми условными средними.
Введем в-ны:
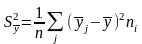

эти в-ны называются межгрупповыми дисперсиями и характеризуют рассеяние условных средних относительно общего среднего выборочного.
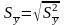 ,
,
 - межгрупповые
среднеквадратичные отклонения
- межгрупповые
среднеквадратичные отклонения
Опр.
Статистическим
коррел-м отношением У на Х наз-ся величина
 ,
где
,
где
Теорема:
 (
( )
)
Д-во:
 -
по
определению,
-
по
определению,
 ,
,

рассмотрим

// ,
зафиксируем
Si
,
зафиксируем
Si
 -
групповая
условная дисперсия
-
групповая
условная дисперсия
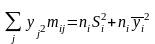

 -
внутригрупповая
дисперсия (среднее значение групповых
дисперсий)
-
внутригрупповая
дисперсия (среднее значение групповых
дисперсий)

получили:

=>


 ,
ЧТД.
,
ЧТД.
10.Условие отсутствия корреляционной связи между св. Функциональная зависимость св.
Будем исследовать тесноту любой, вообще говоря, нелинейной корреляционной связи между СВ X и Y . Пусть имеется корреляционная таблица наблюденных данных СВ X и Y.
X\Y |
y1 |
y2 |
… |
yl |
ni |
x1 |
m11 |
m12 |
… |
m1l |
n1 |
x2 |
m21 |
m22 |
… |
m2l |
n2 |
… |
… |
… |
… |
… |
… |
Xk |
mk1 |
mk1 |
… |
mkl |
nk |
mj |
m1 |
m2 |
… |
ml |
n |
Для
каждого xi
среднее значение соотв.
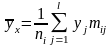
X |
x1 |
x2 |
… |
xk |
|
|
|
… |
|
ni |
n1 |
n2 |
… |
nk |
Введем обозначение . Величины наз. групповыми (условными) средними.
 .
Дисперсия
относительно общего среднего.
.
Дисперсия
относительно общего среднего.
 .
Эти величины характеризуют рассеивание
условных средних относительно общего
среднего выборочного. Они наз. межгрупповыми
дисперсиями.
.
Эти величины характеризуют рассеивание
условных средних относительно общего
среднего выборочного. Они наз. межгрупповыми
дисперсиями.
 ,
,
 -межгрупповые средне квадратичные
отклонения. Статистическим нормальным
отклонением Y
на X
(X
на Y)
наз. величина:
-межгрупповые средне квадратичные
отклонения. Статистическим нормальным
отклонением Y
на X
(X
на Y)
наз. величина:
 (
( ),
), .
Теорема:
0≤
.
Теорема:
0≤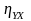 ≤1,
0≤
≤1,
0≤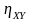 ≤1.
Док-во: док-ем 0≤
≤1,
≥0
– очевидно, т.к.
≤1.
Док-во: док-ем 0≤
≤1,
≥0
– очевидно, т.к.
 и
и
 положительные.
≤1,
положительные.
≤1,
 ,
,
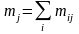 ,
,
 - групповая или условная дисперсия
- групповая или условная дисперсия
 .
.
 .
.
 ,
,
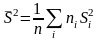 - внутригрупповая дисперсия.
- внутригрупповая дисперсия.
 ,
получили формулу:
,
получили формулу:
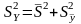 =>
=>
 ,
,
 ,
,
 . Ч.т.д. Теорема:
Если
=0,
то корреляционная связь Y
на X
отсутствует. Док-во:
=0
=>
. Ч.т.д. Теорема:
Если
=0,
то корреляционная связь Y
на X
отсутствует. Док-во:
=0
=> ,
,
 ,
,
 .
Корреляционной связи между X
и Y
нет. Ч.т.д.
.
Корреляционной связи между X
и Y
нет. Ч.т.д.
Функциональная зависимость- это однозначное отображение множества значений С.В. Х в множество значений С.В. Y.
Теорема:
Если
=1,
то СВ Y
и Х функционально зависимы. Док-во:
=1,
то
 ,
.
Было установлено:
.
=>
,
.
Было установлено:
.
=>
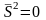 =>
=>
 ,
,
 ,
т.е. выбирая и фиксируя хi
мы получим единственное yj.
Т.е. между x
и y
существует функциональная зависимость.
Ч.т.д.
,
т.е. выбирая и фиксируя хi
мы получим единственное yj.
Т.е. между x
и y
существует функциональная зависимость.
Ч.т.д.