15. Тригонометрический ряд Фур’є

Озн:Тригонометричним рядом на в [-π,π], наз. функціональний ряд вигляду (1), де а₀,а₁,...,b₁,b₂,…- дійсні числа, які наз. коефіцієнтами тригонометричного ряду.(1)

Нехай f(x) подана у вигляді рівномірнозбіжного до неї триг. ряду(1) (2). За власт-ми ряд(2)можна почленно інтегрувати. проінтегр. на[-π,π]

Звідси одержимо:

, (3).

Помножимо тепер обидві частини рівності (2) на coskx і проінтегрувати одержаний вираз на відрізку [-π,π] одержимо:

Звідси одержимо

(4)

Аналогічно помноживши (2) на sinkx і проінтегрувавши одержаний вираз на [-π,π], одержимо: ,

(5).

Озн: Тригонометричний ряд (1) коеф. якого обчислені за формулами (3), (4), (5) наз. рядом Фур’є ф-ї f(x), а самі коеф-ти 3 і 4 наз. коеф. Фур’є.

Розглянемо задачу: нехай задана 2π- періодична ф-ція f(x). Побудуємо для цієї ф-ції ряд Фур’є

(6), де a₀,a_n,b_n – визначається відповідно за формулами (3), (4), (5)

Однак виявляється, що побудований формально ряд (6) взагалі кажучи зовсім не обов’язково буде збігатися до ф-ції f(x), а може збігатися до зовсім іншої ф-ції. Аналогічне явище спостерігалося раніше для рядів Тейлора. Розглянемо далі теорему в якій наведені умови за яких ряд Фур’є ф-ції f(x) збігається саме до ф-ції f(x).

Теорема 1 (б/д)

Якщо ф-ю f(x) можна подати у вигляді рівномірно збіжною тригоном. ряду (2) то це подання єдине і данний тригоном. ряд є рядом Фур’є цієї ф-ї.

Озн

Ф-цію f(x) наз. Кусково-монотонною на відрізку [a,b], якщо існує таке розбиття відрізка на n частин a=x₀<x₁<…<x_n=n, що на кожн. з від-ку [x_i-1; x_i] ф-ція f(x) монотонною.

Теорема 2: Нехай f(x) обмежена, 2π- періодична і кузково-монотонна ф-я на всій осі, тоді ряд Фур’є ф-ї f(x) є збіжним на всій числовій осі і сума S(x) цього ряду дорівнює значенню ф-ї f(x), якщо х₀-точка розриву ф-ї f(x), то

.

Зауваження: Крім того виявляється, що випудку, коли ф-ція f(x) є парною, або непарною задача знаходження коєфіц. Фур’є значно спрощ. Так для парної ф-ції f(x) ряд Фур’є містить лише косинуси.

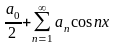
і коефіц. Фур’є обчислюємо:

,

Для непарної ф-ції ряд Фур’є містить лише синуси

n=1,2,…

b_n=2/π n=1,2,… коеф.

Це невипадково, оскільки таке подання відображає хар-тер ф-ції. Для парної ф-ції ряд Фур’є скл. З парних ф-цій косинусів, а для непарних – з непарних ф-цій синусів.

16. Подвійний інтеграл умови його існування і властивості.

Нехай функция задана у замкненій

обмеженій області D, границя якої складається із числа неперервних кривих.

Розіб’ємо область D на n частин – неперервними кривими так щоб ці частини не мали спільних внутрішніх точок. Площу позначимо відповідно через .

Візьмемо у кожній з цих частин довільні точки: і побудуємо суму

Сума (1) наз. інтегральною сумою ф-ції по області D.

Зрозуміло що можна побудувати скільки завгодно таких сум в залежності від того як розіб’ємо D на частини і як вибираємо точки .

Діаметр обмеженої області G наз. найбільша відстань між двома точками межі цієї області.

Позначимо через діаметр області G. Позначимо через найбільший з діаметрів множин .

Озн. Якщо при існує границя інтегральних сум (1), яка не залежить від способу розбиття D на частини вибору точок в кожній з них цю границю називають подвійним інтегралом по області D і позначають символом .

В цьому позначенні D – область інтегрування, - підінтегральна ф-ція, х та у – змінні інтегрування, dS – елемент площі. Тобто за означенням подвійний інтеграл

З означення подвійного інтеграла випливає, що він не залежить від способу розбиття області

D, тому в декартових координатах найбільш

вдалим є розбиття області D прямими, що паралельні координатним осям

, тому подвійний інтеграл у цьому випадку позначають як . Якщо у формулі (2) взяти , то одержимо формулу для обчислення площі області D: .

Геометричний зміст подвійного інтегралу: Якщо подвійний інтеграл по області D = об’єму циліндричного тіла яке обмежене зверху поверхнею знизу областю D, в площині хоу з боків циліндричною поверхнею напрямна якої збігається з межою області D, а твірні паралельні осі OZ.

Теорема: Якщо ф-ція неперервна у замкненій обмеженій області D, то вона інтегрована в цій області.

Порівняємо тепер позначення (2) з позначенням визначеного інтегралу:

Конструктивно ці означення однакові: і в 2, і в 3 ідеться що замкнену обмежену множину, в 2 це область D, в 3 відрізок потім ця множина ділиться на частини, в кожній із них вибирається точка і обчислюється значення ф-ції в цій точці, потім це значення множиться на міру відповідної множини. В (2) це є 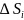– площа множини , а в (3) - - довжина відрізку . В утворених інтегральних сумах знаходиться границя коли міра частин області прямує до 0. Враховуючи все це можна зробити висновок, що властивості подвійного інтегралу аналогічні визначеному, наведемо їх без доведення.

Властивості:

1) Сталий множник можна виносити за знак подвійного інтегралу .

2) Подвійний інтеграл від суми (різниці) інтегрованих в області D ф-цій = сумі (різниці) подвійних інтегралів цих ф-цій .

3) Якщо ф-ція інтегровна в області D і для всіх точок із D, .

4) Якщо ф-ція і інтегровні в області D і для точок цієї області , то .

5) Якщо область D поділити неперервною кривою на частини і , які не мають спільних внутрішніх точок і ф-ція інтегровна в області D, то

6) Якщо ф-ція неперервна у замкненій обмеженій області D, то справедлива нерівність , де m і M відповідно найменше і найбільше значення ф-ції , яких вона набуває в області D. - площа області D.

7) Якщо ф-ція неперервна у замкненій обмеженій області D. То існує точка , така що