7.3 Решение смешанной задачи для уравнения гиперболического типа методом сеток

Рассмотрим уравнение колебания однородной и ограниченной струны.

Задача состоит в отыскании функции u(x,t) приt>0, удовлетворяющей уравнению гиперболического типа

,

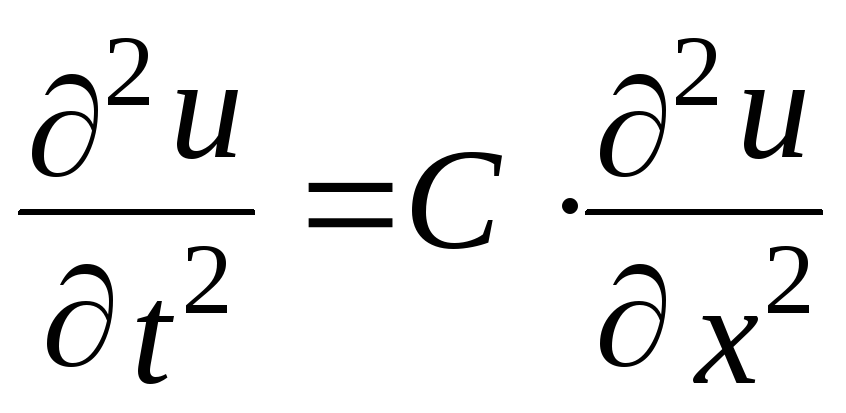(7.12)

где: 0<x<a; 0<t<T,

начальным условиям

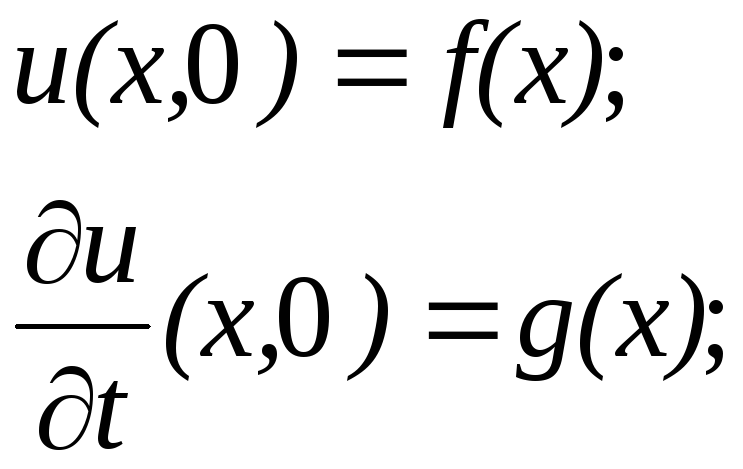
0  x a

(7.13)

и краевым условиям

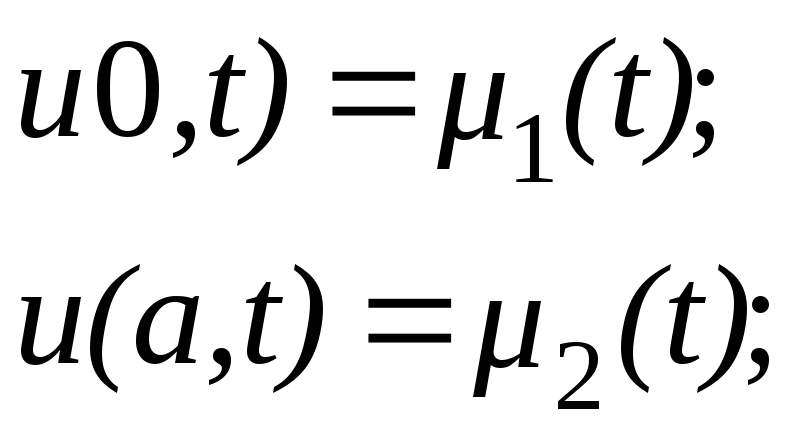
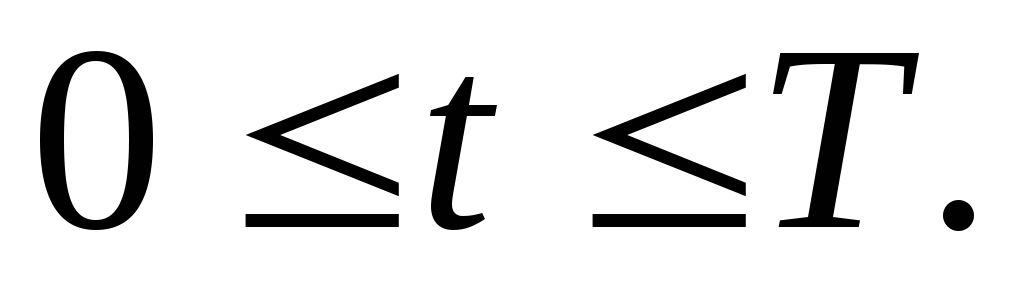
(7.14)

Заменим Снасtи получим уравнение

и в дальнейшем будем считать С=1.

Для построения разностной схемы решение задачи (7.12)-(7.14) построим в области сетку;i=0,1,…,n;;;j=0,1,…,m;m=T.

Аппроксимируем (7.12) разностными производными второго порядка точности относительно шага

.

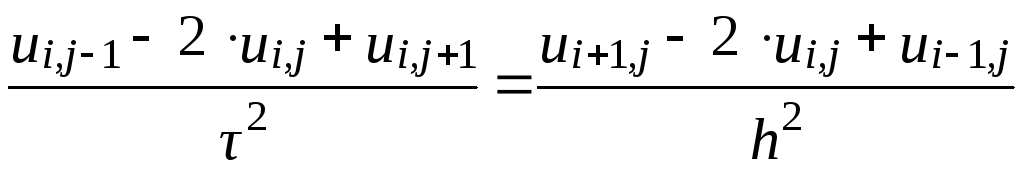(7.15)

Полагая =/hперепишем (7.15), выразивU_i,j+1.Таким образом получим трехслойную разностную схему

,

(7.16)

где: i=1,…,n;j=1,…,m. Задаем нулевые граничные условия₁(t)=0, ₂(t)=0. Тогда в (7.16),для всехj.

Схема (7.16) называется трехслойной, т.к. она связывает значения искомой функции на трех временных слоях j-1,j,j+1.

Численное решение задачи состоит в вычислении приближенных значений решенияu(x,t) в узлахприi=1,…,n; j=1,…,m.Алгоритм решения основан на том, что решение на каждом следующем слое (j=2,3,..,n) можно получить пересчетом решений с двух предыдущих слоев (j=0,1,..,n-1) по формуле (7.16). Приj=0 решение известно из начального условия. Для вычисления решения на первом слое (j=1) положим

,

(7.17)

тогда ,i=1,2,…,n. Теперь для вычисления решений на следующих слоях можно использовать формулу (7.16).

Описанная схема аппроксимирует задачу (7.12)-(7.14) с точностью O(+h). Невысокий порядок аппроксимации по объясняется грубостью аппроксимации по формуле (7.17).

Схема будет устойчивой, если выполнено условие .

Лабораторная работа № 1 Решение систем линейных алгебраических уравнений

Точные методы

Метод Гаусса

Входные параметры: n—целое положительное число, равное порядку n системы; а — массив изnхnдействительных чисел, содержащий матрицу коэффициентов системы (а(1) = а₁₁, а(2) =a_12…а(n) = а_n1, а(n+ 1) = а₁₂, .... а(n хn) = а_nn);b— массив изnдействительных чисел, содержащий столбец свободных членов системы (b(1) =b₁,b(2)=b_2,…b(n)=b_n).

Выходные параметры: b—массив изnдействительных чисел (он же входной); при выходе из программы содержит решение системыb(l) =x₁,b(2) =x₂, …b(n) = х_n;error—признак правильности решения (код ошибки): еслиks= 0, то в массивеbсодержится решение системы, еслиerror= 1, исходная система не имеет единственного решения (определитель системы равен нулю).

Перед обращением к подпрограмме SIMQнеобходимо:

1) описать массивы а и b. Если система содержитnуравнений, то массив а должен содержатьn² элементов, а массивb–nэлементов;

2) присвоить значение параметру n, который равен числу уравнений системы;

3) присвоить элементам массивов а и bзначения коэффициентов системы следующим образом:a(l) =a₁₁, а(2) = а₂₁, а(3) = а₃₁,…а(n) = а_n1а(n+1) = а₁₂, а(n+2) = а₂₂… а(nxn) = а_nn.b(1) =b₁,b(2)=b_2,…b(n)=b_n

4) проверить соответствие фактических параметров по типу и порядку следования формальным параметрам подпрограммы SIMQ. Параметры а иb- величины вещественного типа, n иerror- целого типа.

Задание. Используя программу SIMQ, решить заданную систему трех линейных уравнений. Схема алгоритма приведена на рисунке 13.