Причем- для первой задачи.

6.6 Решение двухточечной краевой задачи для линейного уравнения второго порядка сведением к задаче Коши

Запишем линейное уравнение второго порядка в виде

,

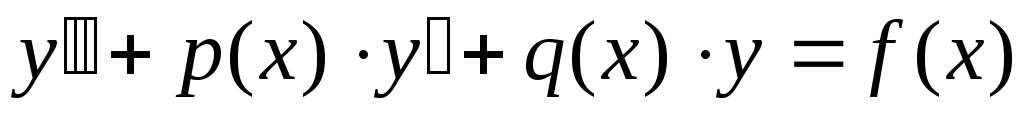(6.40)

где: p, q, f-известные непрерывные функции на некотором отрезке [a,b].

Требуется найти решение уравнения (6.40), удовлетворяющее заданным краевым условиям

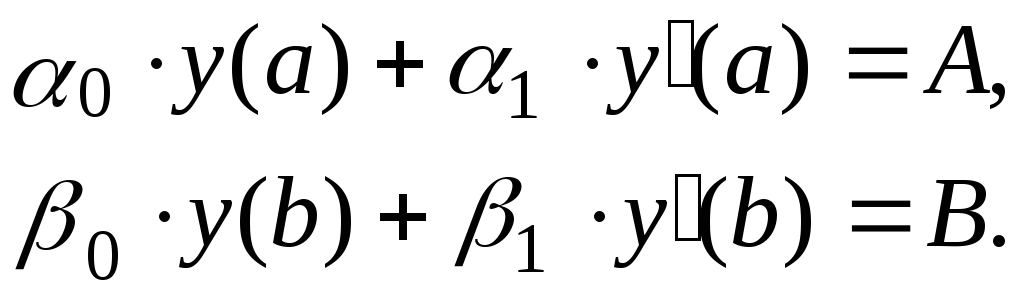
(6.41)

Причем константы иодновременно не равны нулю

Решение задачи (6.40), (6.41) будем искать в виде линейной комбинации

y=Cu+V,

где С - константа, u-общее решение соответствующего однородного уравнения

,

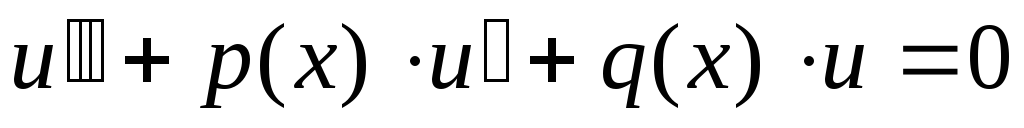(6.42)

а V-некоторое частное решение неоднородного уравнения

.

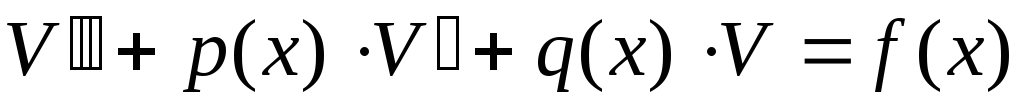(6.43)

Потребуем ,чтобы первое краевое условие было выполнено при любом C,

,

откуда следует, что ,.

Тогда

,

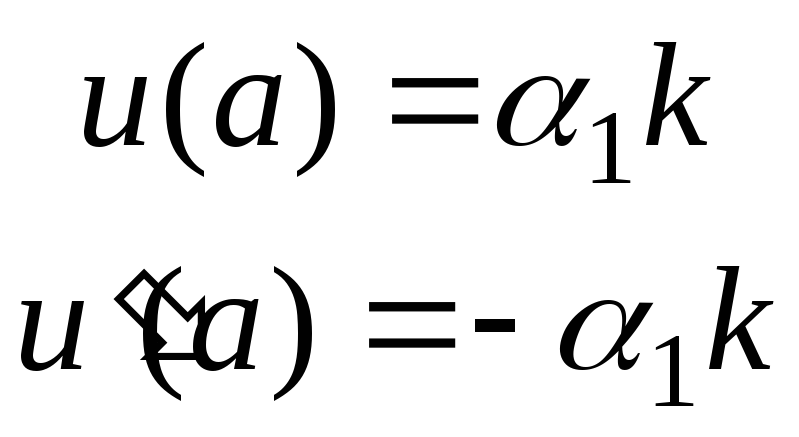(6.44)

где k- некоторая константа, не равная нулю. Значение функцииVи ее производная в точкеа

,

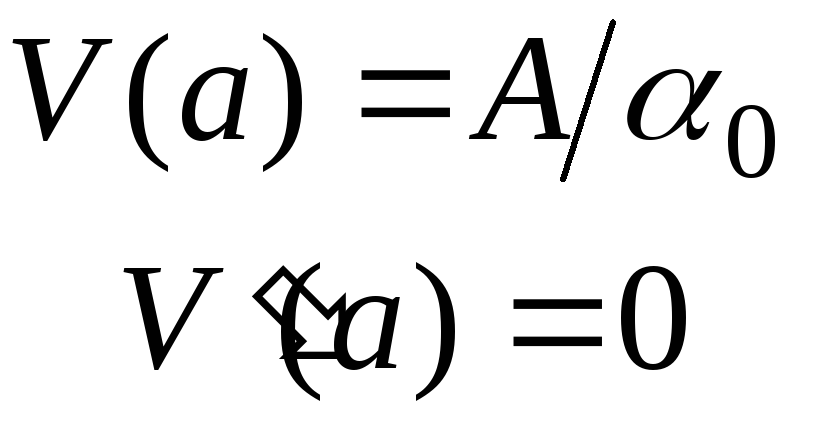(6.45)

если коэффициент и

,

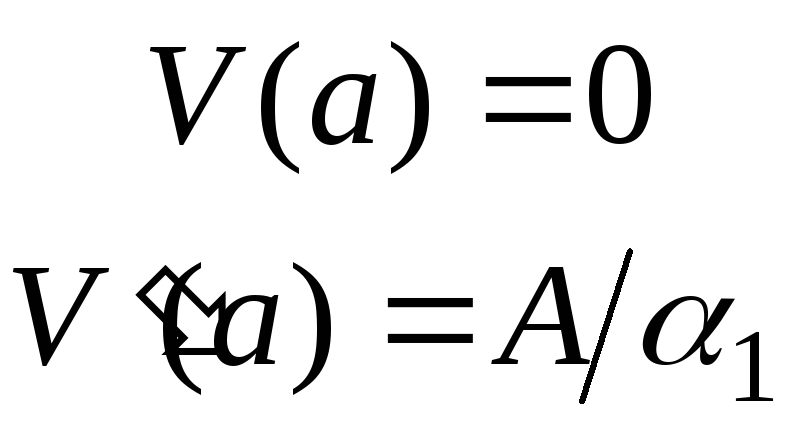(6.46)

если коэффициент .

Из этих рассуждений следует, что функция u- есть решение задачи Коши для однородного уравнения (6.42) с начальными условиями (6.44), а функцияV- есть решение задачи Коши для неоднородного уравнения (6.43) с начальными условиями (6.45) или (6.46) в зависимости от условий. КонстантуCнадо подобрать так, чтобы выполнялись условия (6.41) (вторая строчка) в точкеx=b

.

Отсюда следует, что

,

где знаменатель не должен быть равен нулю, т. е.

.

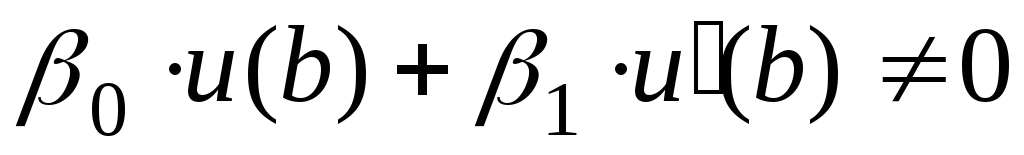(6.47)

Если условие (6.47) выполнено, то краевая задача (6.35), (6.36) имеет единственное решение. Если же (6.47) не выполняется, то краевая задача (6.35), (6.36) либо не имеет решения, либо имеет бесконечное множество решений.

6.7 Методы численного решения двухточечной краевой задачи для линейного уравнения второго порядка

6.7.1 Метод конечных разностей

Рассмотрим линейное дифференциальное уравнение

(6.48)

с двухточечными краевыми условиями

; ,

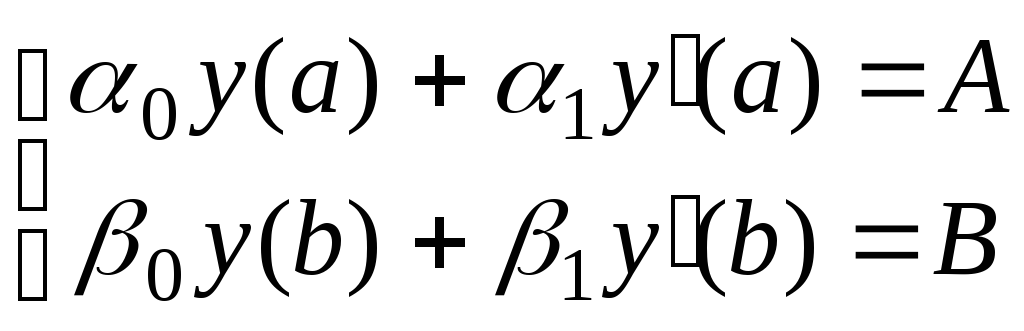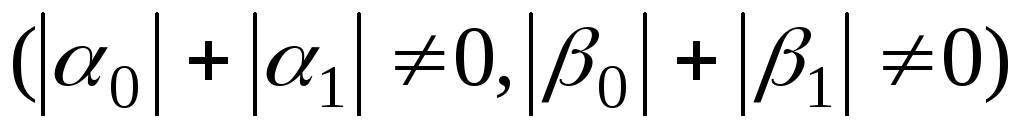(6.49)

где: p, q, f-известные непрерывные функции на некотором отрезке [a,b].

Одним из наиболее простых методов решения этой краевой задачи является сведение ее к системе конечно-разностных уравнений.

Основной отрезок [a,b] делим на n- равных частей с шагомh=(b-a)/n, то есть рассматриваем равномерную сетку,i=0,1,…,n. Производные в исходном уравнении (6.48) заменяем конечно-разностными отношениями. Для внутренних точек

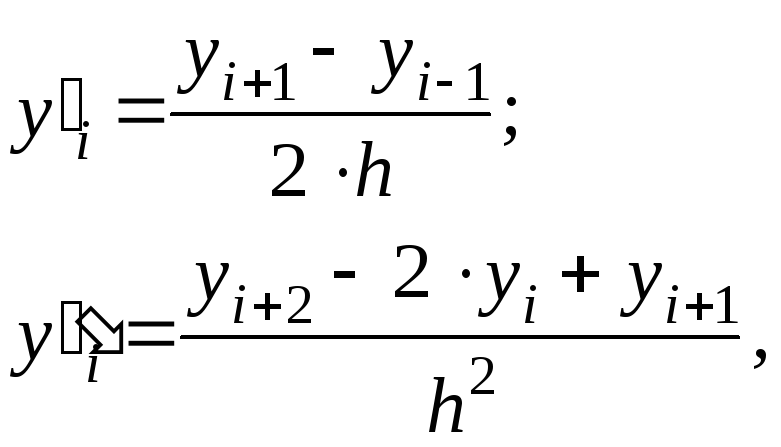
(6.50)

где i=1,...,n-1.

Для граничных точек и, чтобы не выходить за границы отрезка, производные заменяем отношениями

.

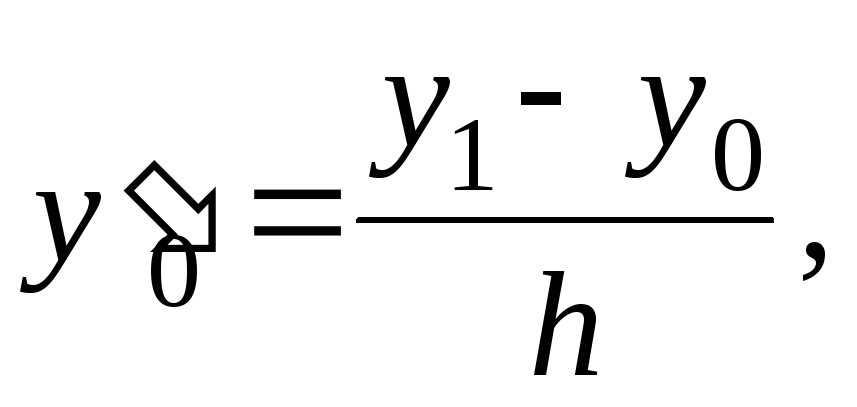
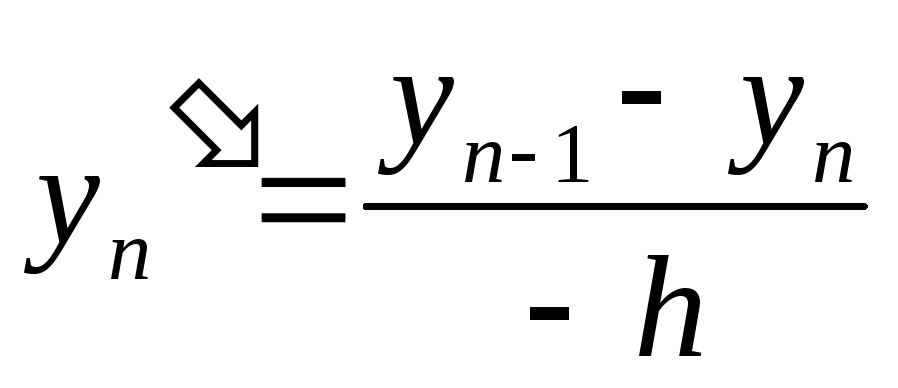(6.51)

Используя отношения (6.50), (6.51) исходное дифференциальное уравнение (6.48) аппроксимируем конечно-разностными уравнениями

,

(6.52)

где i=1,...,n-1. Учитывая краевые условия, получим еще два уравнения

.

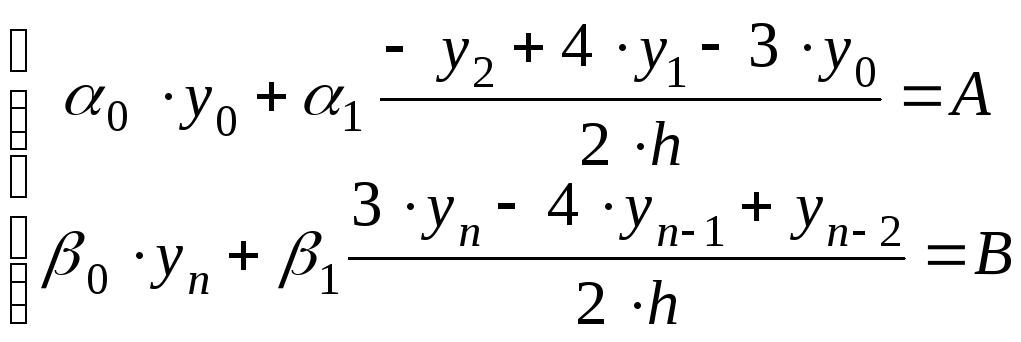(6.53)

Таким образом получена линейная система n+1 уравнений сn+1 неизвестными, представляющими собой значения искомой функциив точках. Решив эту систему, получим таблицу значений искомой функцииy.

6.7.2 Метод прогонки (одна из модификаций метода Гаусса)

При применении метода конечных разностей к краевым задачам для дифференциальных уравнений второго порядка получается система линейных алгебраических уравнений с трехдиагональной матрицей, т.е. каждое уравнение системы содержит три соседних неизвестных. Для решения таких систем разработан специальный метод – «метод прогонки».

Для этого систему (6.52) перепишем в виде

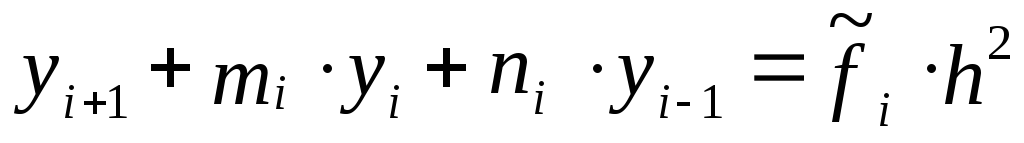для внутренних точек (i=1,…,n-1),

(6.54)

где: ;;.

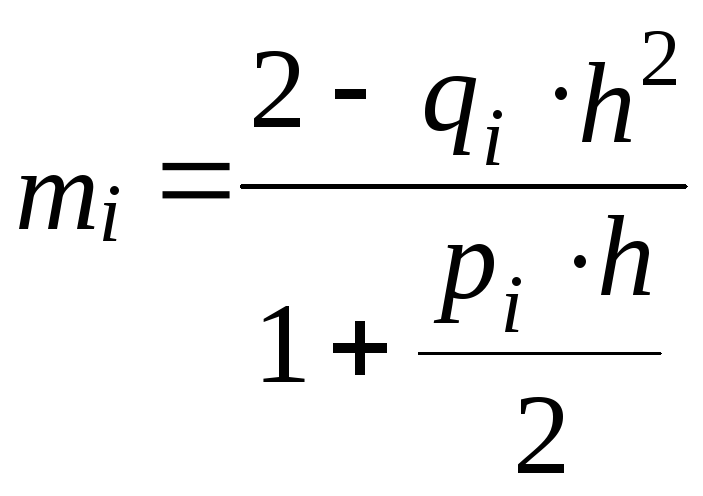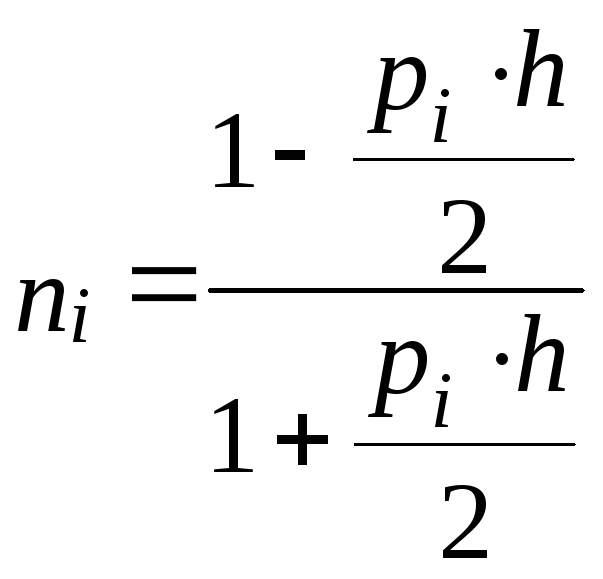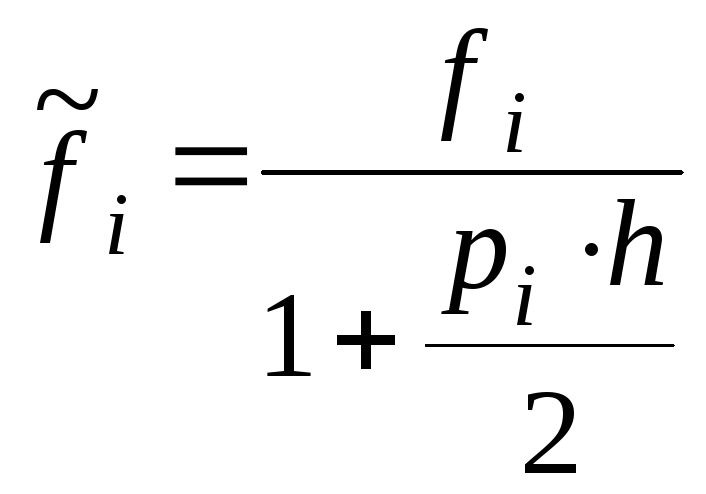На концах отрезка x₀=a и x _n=b производные заменяем разностными отношениями

и .

Учитывая эту замену получим еще два уравнения

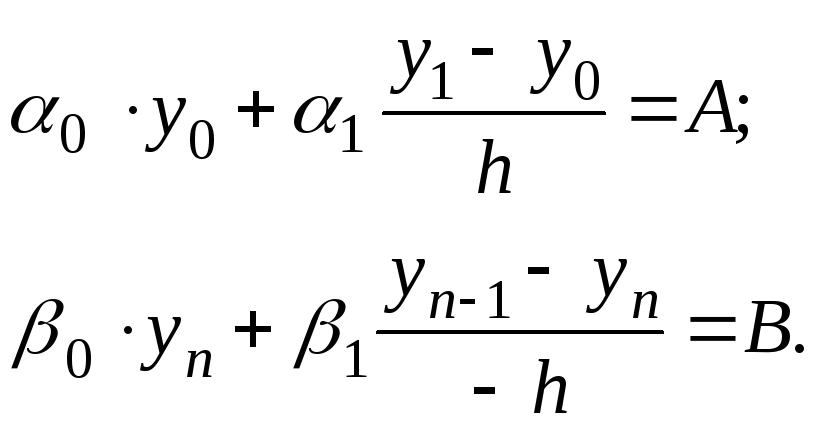
(6.55)

Обратим внимание на внешний вид записи системы (6.54), (6.55). В каждом уравнении системы присутствует три ненулевых элемента. В первом и последнем - по два ненулевых коэффициента.

Разрешая уравнение (6.54) относительно , получим

.

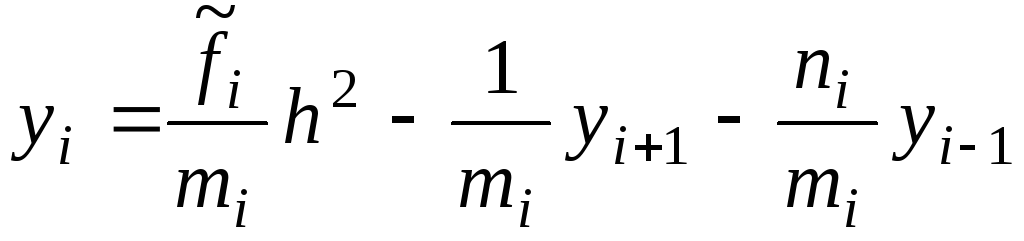(6.56)

Предположим, что с помощью полной системы (6.54), (6.55) из уравнения (6.56) исключена неизвестная . Тогда это уравнение примет вид

,

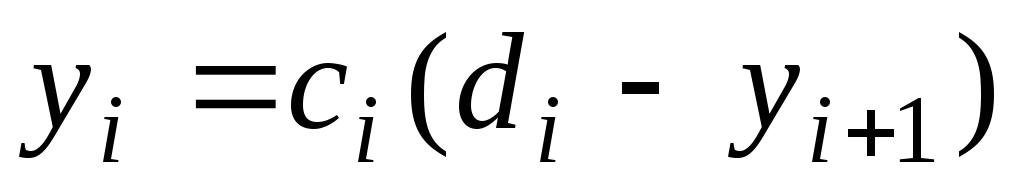(6.57)

где: - некоторые коэффициенты;i=1,2,…,n-1. Отсюда

.