4.1 Прямые методы

4.1.1 Метод Леверрье

Метод разделяется на две стадии:

- раскрытие характеристического уравнения,

- нахождение корней многочлена.

Пусть det(A-E) - есть характеристический многочлен матрицы А={a_ij} (i,j=1,2,…,m), т.е., и₁,_2,…,_m- есть полная совокупность корней этого многочлена (полный спектр собственных значений).

Рассмотрим суммы вида (k=1,2,…,m), т.е.

,

(4.3)

где - след матрицы.

В этом случае при kmсправедливы формулы Ньютона для всех (1km)

,

(4.4)

Откуда получаем

при k=1р1 = -S1, при k=2 р2 = -1/2 * (S2 + р1*S1), . . . . . . . . . . . . . . при k=m рm = -1/n * (Sm + р1*Sm-1 + р2*Sm-2 + ... + рm-1*S1).

(4.5)

Следовательно, коэффициенты характеристического многочлена р_iможно определить, если известны суммыS₁,S₂,...,S_m. Тогда схема алгоритма раскрытия характеристического определителя методом Леверрье будет следующей:

1) вычисляем степень матрицы: А^к=А^к-1*Адляk=1,…,m;

2) определяют S_k- суммы элементов стоящих на главной диагонали матрицА^к;

3) по формулам (4.5) находят коэффициенты характеристического уравнения р_i(i=1,2,…,m).

4.1.2 Усовершенствованный метод Фадеева

Алгоритм метода:

1) вычисляют элементы матриц A₁,A₂,..,A_m:

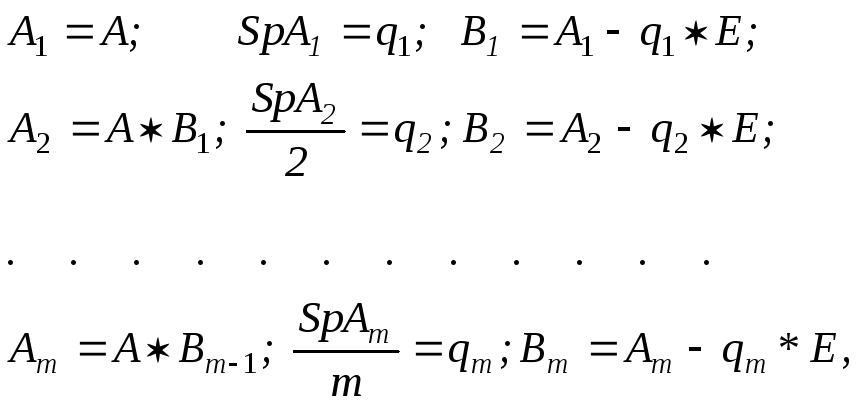
(в конце подсчета B_mнулевая матрица для контроля);

2) определяют коэффициенты характеристического уравнения р_i

q₁ = -р₁, q₂ = -р₂,..., q_m = -р_m.

Существуют и другие методы раскрытия характеристического определителя: метод Крылова, Данилевского и др.

4.1.3 Метод Данилевского

Две матрицы A и B называются подобными, если одна получается из другой путем преобразования с помощью некоторой не вырожденной матрицы S:

B=S^-1*AS,

если это равенство справедливо, то матрицы A и B подобны, а само преобразование называется преобразованием подобия (переход к новому базису в пространстве m - мерных векторов).

Пусть y- результат применения матрицы A к векторух

y=A*х.

Сделаем замену переменных:

x=S*x' , y=S*y'.

Тогда равенство y=A*хпреобразуется к виду

y'=S^-1*A*S*x'.

В этом случае матрица B и матрица A имеют одни и те же собственные числа. Это можно легко увидеть раскрыв определитель

.

Следовательно, матрицы A и B - подобные, имеют одни и те же собственные значения. Но собственные векторы хих’– не совпадают, они связаны между собой простым соотношением

х = S*х'.

Такую матрицу A с помощью преобразования подобия или же последовательности таких преобразований можно привести к матрице Фробениуса вида:

.

Детерминант матрицы F det (F) можно разложить по элементам первой строки:

.

Тогда коэффициенты характеристического многочлена матрицы А будут р₁ = f₁₁ , p₂ = f_12,…, p_n = f_1m.

Второй случай. Матрицу А преобразованием подобия можно привести к матрице В верхнего треугольного вида

.

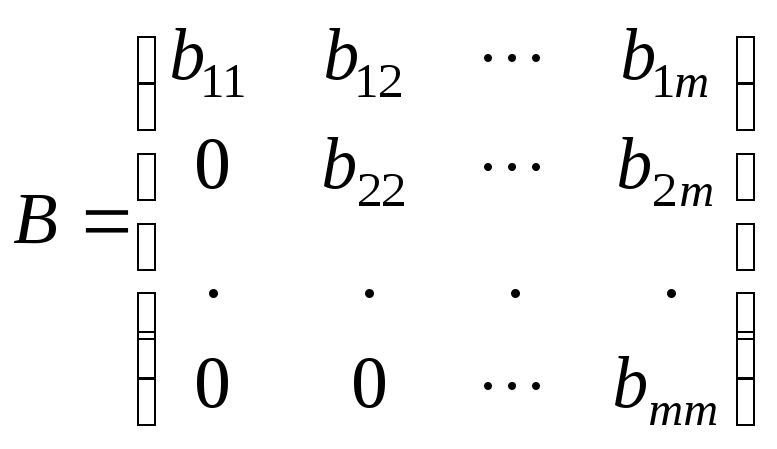Тогда собственными числами будут диагональные элементы матрицы B:

.

Третий случай. Матрицу A с помощью преобразования подобия можно привести к Жордановой форме

,

где _i- собственные числа матрицы A; S_i- константы (0 или 1); если S_i=1, то_i=_i+1.

К четвёртому случаю относятся матрицы, которые с помощью преобразования подобия можно привести к диагональному виду (матрица простой структуры):

,
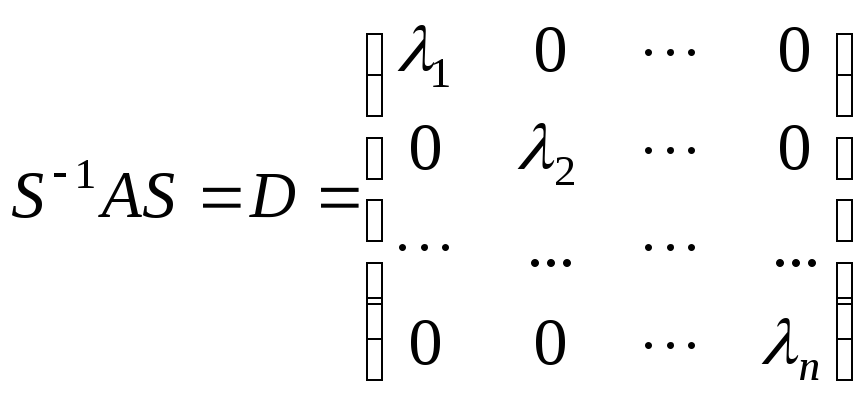
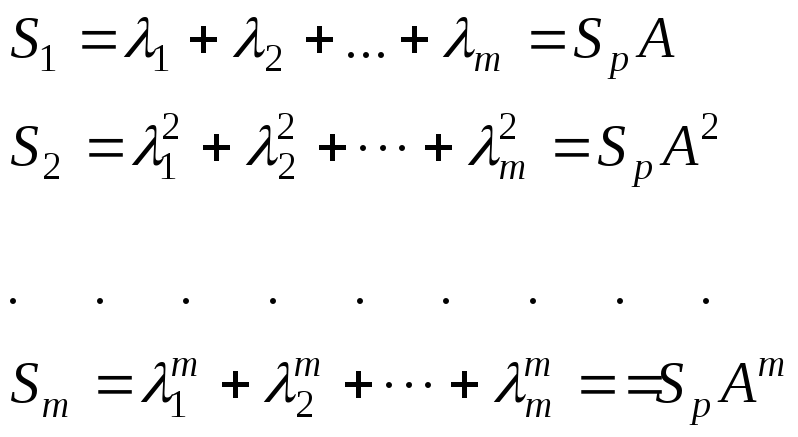