7.1 Метод сеток для решения смешанной задачи для уравнения параболического типа (уравнения теплопроводности)

Смешанная задача означает, что следует найти искомую функцию, удовлетворяющую заданному уравнению в частных производных, краевым, а так же начальным условиям.

Рассмотрим смешанную задачу для однородного уравнения теплопроводности

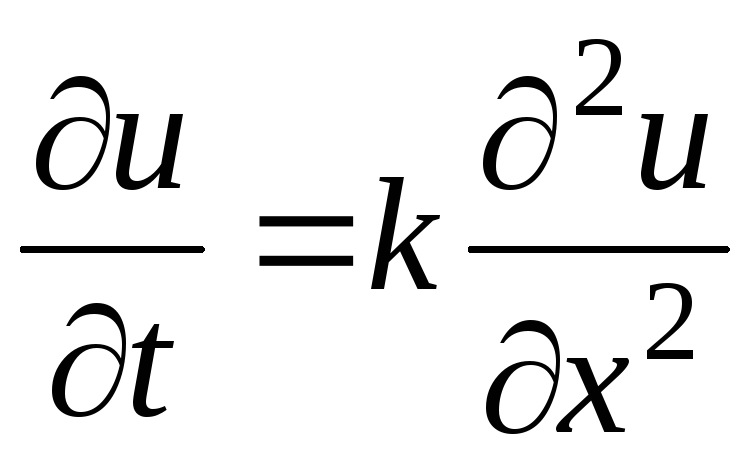, k=const>0.

(7.4)

Задано начальное условие

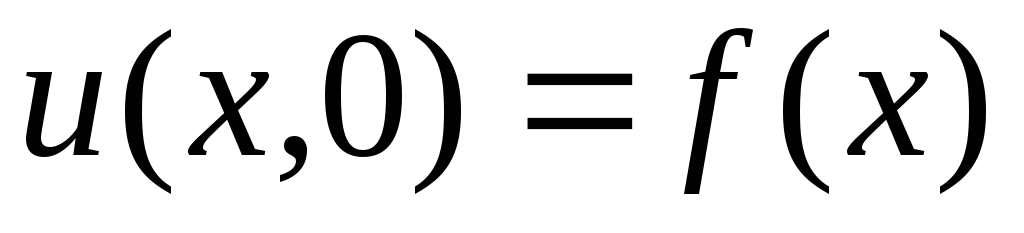
(7.5)

и заданы краевые условия первого рода

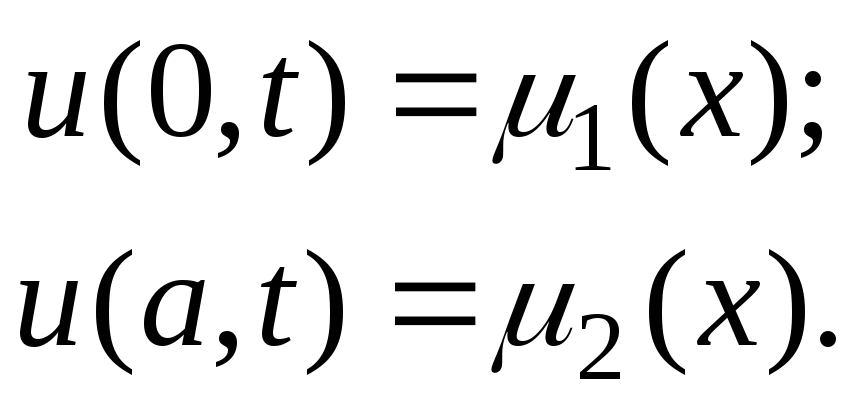
(7.6)

Требуется найти функцию u(x,t), удовлетворяющую в областиD(0<xa, 0<tT) условиям (7.5) и (7.6). Физически это можно представить как стержень, на концах которого поддерживается требуемый температурный режим, заданный условиями (7.6).

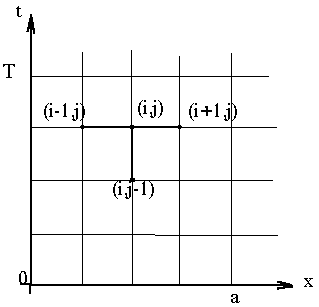
Рисунок 10 – Неявная схема

При проведении замены получим , т.е.k=1. Задача решаетсяметодом сеток: строим в областиDравномерную сетку с шагомhпо осиxи шагомпоt(см. рисунок 10).

Приближенное значение искомой функции в точке -обозначим через. Тогда ;; i=0,1,...,n; ;

j=0,1,...,m;. Заменим производные разностными отношениями

;

.

В результате получим неявную двухслойную схему с погрешностью O(+h²)

.

Используя подстановку , выразим из этой схемыu_i,j-1

,

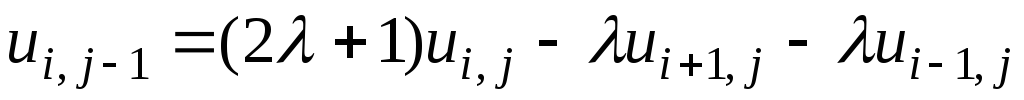(7.7)

где: u_0,j=₁(t_j); u_n,j=₂(t_j).

Получаем разностную схему, которой аппроксимируем уравнение (7.4). Эта схема (7.7) неявная, и выглядит так, как показано на рисунке 10. При построении схемы (7.7) получается система линейных уравнений с трехдиагональной матрицой. Решив ее любым способом (в частности, методом прогонки), получаем значения функции на определенных временных слоях. Так, на нулевом временном слое используем начальное условие U_i,0=f(x_i), т.к.j=0. Эта неявная схема более устойчива для любых значений параметра>0.

Есть и явная схема (рисунок 11), но она устойчива только при , т.е. при.

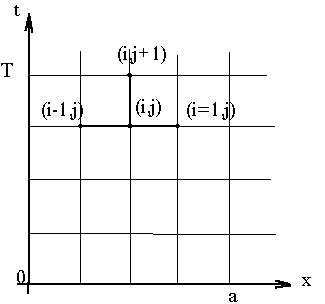
Рисунок 11 - Явная схема

7.2 Решение задачи Дирихле для уравнения Лапласа методом сеток

Рассмотрим уравнение Лапласа

.

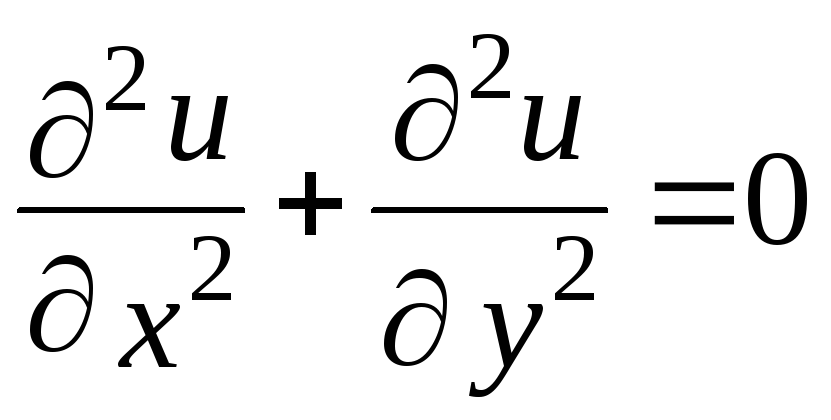(7.8)

Уравнение (7.8) описывает распространение электромагнитных волн(полей). Будем рассматривать уравнение Лапласа в прямоугольной области с краевыми условиями

; ;;,

где -заданные функции. Заметим, что чаще всего область бывает не прямоугольной.

Введем обозначения u_ij=u(x_i,y_j). Накладываем на прямоугольную область сетку;i=0,1,…,n;;j=0,1,…,m. Тогда,.

Частные производные аппроксимируем по формулам

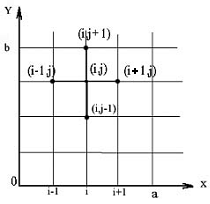
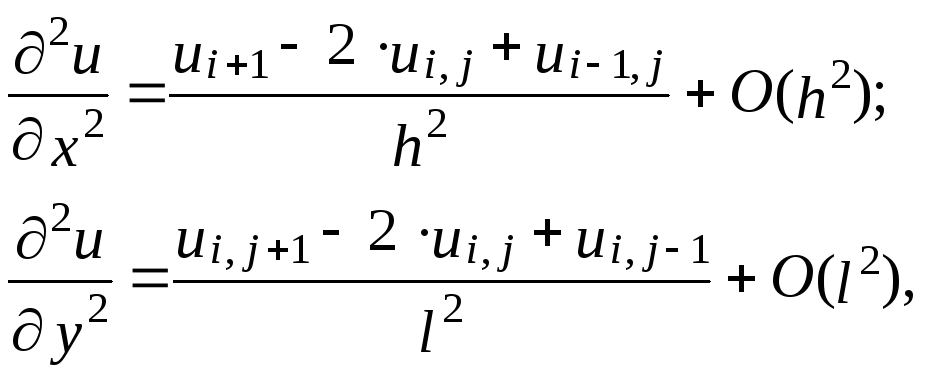
и заменим уравнение Лапласа конечно-разностным уравнением

Рисунок 12 – Схема “крест”

,

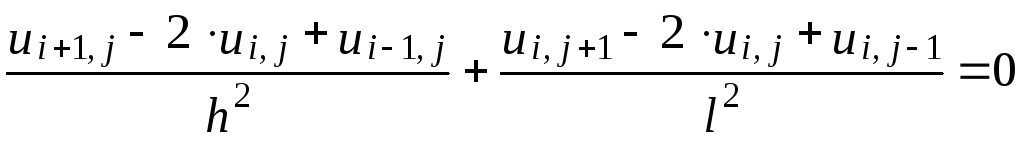(7.9)

где: i=1,…,n-1,j=1,...,m-1 (т.е. для внутренних узлов).

Погрешность замены дифференциального уравнения разностным составляет величину О(). Выразимu_i,jприh=l, и заменим систему

(7.10)

Получаем систему (7.10) линейных алгебраических уравнений, которые можно решить любым итерационным методом (Зейделя, простых итераций и т.д.). При этом построении системы использовалась схема типа “крест”(рисунок 12). Строим последовательность итераций по методу Гаусса-Зейделя

,

где s-текущая итерация.

Условие окончания итерационного процесса

.

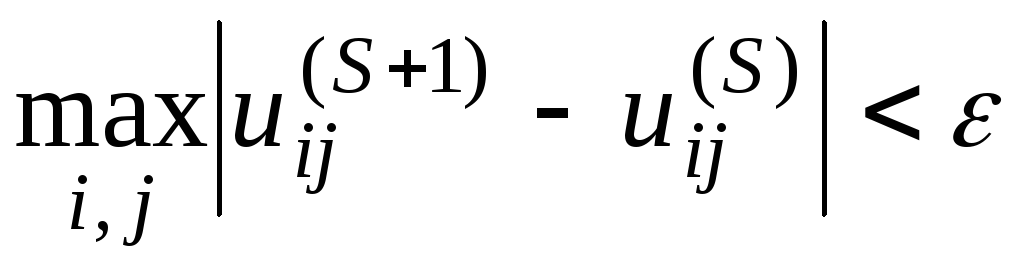
(7.11)

Условие (7.11) ненадежно и на практике используют другой критерий

где .

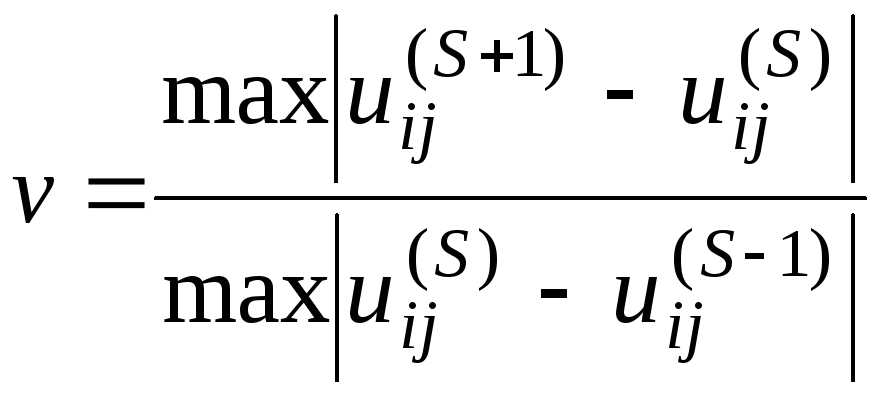Схема “крест “- явная устойчивая схема ( малое изменение входных данных ведет к малому изменению выходных данных).