Подставляя это выражение в уравнение (6.54), получим

,

а отсюда

.

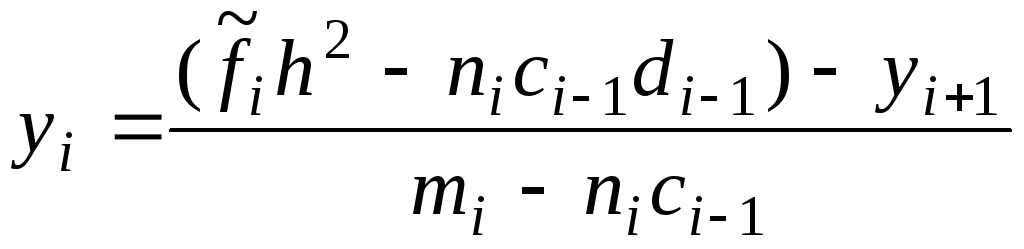(6.58)

Сравнивая (6.57) и (6.58), получим для определения ирекуррентные формулы

; i=1,…,n-1.

(6.59)

Из первого краевого условия (6.55) и из формулы (6.57) при i=0 находим

; .

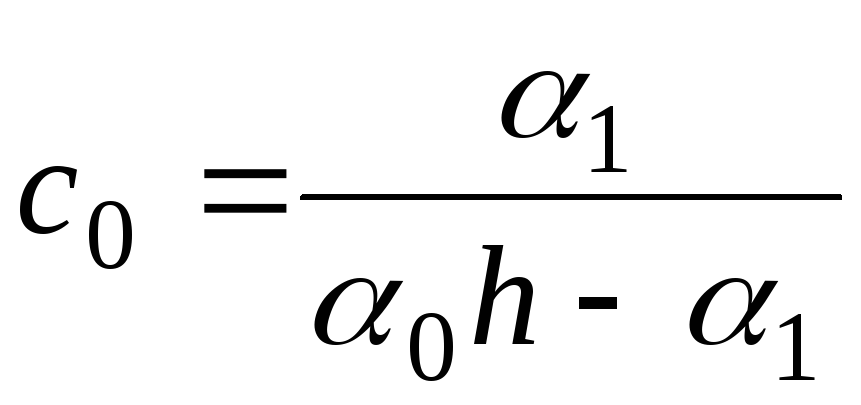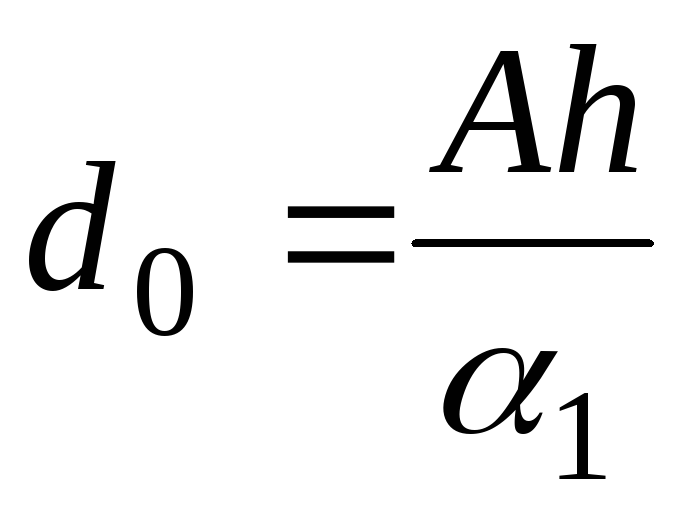(6.60)

На основании формул (6.59), (6.60) последовательно определяются коэффициенты ,(i=1,…,n-1) доивключительно (прямой ход).

Обратный ход начинается с определения . Для этого из второго краевого условия (6.55) и из формулы (6.51) приi=n-1 найдем

.

(6.61)

Далее по формуле (6.57) последовательно находим .

Заметим, что метод прогонки обладает устойчивым вычислительным алгоритмом.

7 Приближенное решение дифференциальных уравнений в частных производных

В реальных физических процессах искомая функция зависит от нескольких переменных, а это приводит к уравнениям в частных производных от искомой функции. Как и в случае обыкновенных дифференциальных уравнений(ОДУ), в этом случае для выбора одного конкретного решения, удовлетворяющего уравнению в частных производных, необходимо задавать дополнительные условия (т.е. краевые условия ). Чаще всего такие задачи на практике не имеют аналитического решения и приходится использовать численные методы их решения, в том числе метод сеток, метод конечных разностей и так далее. Мы будем рассматривать класс линейных уравнений в частных производных. В общем виде эти уравнения записываются в виде

,

(7.1)

где: A, B, C, a, b, c-заданные непрерывные функции двух переменных, имеющие непрерывные частные производные,u-искомая функция. Для сокращения записи введем обозначения

; ; ;;.

Будем рассматривать упрощенную форму записи (7.1) вида

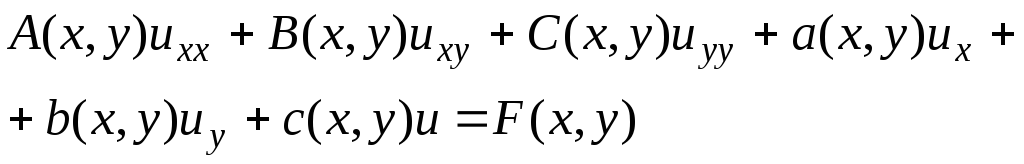
(7.2)

и рассмотрим частный случай (7.2), когда a=b=c=F0, т.е.

.

(7.3)

Путем преобразований уравнение (7.3) может быть приведено к каноническому виду (к одному из трех стандартных канонических форм) эллиптическому типу, гиперболическому типу, параболическому типу. Причем тип уравнения будет определяться коэффициентами А, В, С, аименно – знаком дискриминанта

D=B²-4AC.

Если D<0, то имеем уравнение эллиптического типа в точке с координатамиx, y; еслиD=0, то (7.3)-параболического типа; еслиD>0, то (7.3)-гиперболического типа; еслиDне сохраняет постоянного знака, то (7.3)-смешанного типа.

Замечание.ЕслиА, В, С- константы, тогда каноническое уравнение (7.3) называется полностью эллиптического, параболического, гиперболического типа.

Введем понятие оператора Лапласа для сокращенной записи канонических уравнений вида

.

Используя это определение, запишем сокращенные канонические уравнения всех трех типов

1. u=0. Это уравнение эллиптического типа, так называемое уравнение Лапласа. В механике это уравнение описывает стационарные тепловые поля, установившееся течение жидкости и т.д.

2.u=-f, гдеf-заданная непрерывная функция. Это уравнение Пуассона имеет эллиптический тип и описывает процесс теплопередачи с внутренним источником тепла.

3. , гдеa-константа. Не во всех уравнениях в качестве переменных будут выступать стандартные переменныеx, y. Может быть также переменная времени. Это уравнение диффузии описывает процесс теплопроводности и является уравнением параболического типа.

4. ,а-константа. Это уравнение гиперболического типа - так называемое волновое уравнение и оно описывает процесс распространения волн.