5.4 Аппроксимация функций методом наименьших квадратов

К такой задаче приходят при статистической обработке экспериментальных данных с помощью регрессионного анализа. Пусть в результате исследования некоторой величины xзначениямпоставлены в соответствие значениянекоторой величины у.

Требуется подобрать вид аппроксимирующей зависимости y=f(x),связывающей переменныех и у.Здесь могут иметь место следующие случаи. Во-первых: значения функцииf(x)могут быть заданы в достаточно большом количестве узлов; во-вторых: значения таблично заданной функции отягощены погрешностями. Тогда проводить приближения функции с помощью многочлена нецелесообразно, т.к.

- это неудобно делать, поскольку число узлов велико и пришлось бы строить несколько интерполяционных многочленов;

- построив интерполяционные многочлены, мы повторили бы те же самые ошибки, которые присущи таблице.

Будем искать приближающую функцию из следующих соображений:

1. приближающая функция не проходит через узлы таблицы и не повторяет ошибки табличной функции;

2. чтобы сумма квадратов отклонений приближающей функции от таблично заданной была минимальной.

у отклонения

х₀х₁х_n-1х_nх

Рисунок 6 – Графическое изображение отклонений

Рассмотрим линейную задачу наименьших квадратов.

Пусть даны функции , назовем их базисными функциями. Будем искать приближающую (аппроксимирующую) функцию в виде линейной комбинации

. (5.11)

Такая аппроксимация называется линейной, а Ф_m(х) – обобщенный многочлен. Согласно критерию метода наименьших квадратов вычислим сумму квадратов отклонений таблично заданной функции от искомого многочлена в узлах:

. (5.12)

Но нам неизвестна степень обобщенного многочлена. Подберем ее так, чтобы было наименьшим и:

- аппроксимирующая кривая не проходила через узлы таблицы;

- получить приближение с заданной степенью точности.

Выражение можно рассматривать как функцию от неизвестных. Нас интересует, при каких значениях, значениебудет минимально.

Для этого воспользуемся условием существования экстремума, а именно, найдем частные производные от по всем переменными приравняем их к нулю. Получим систему вида:

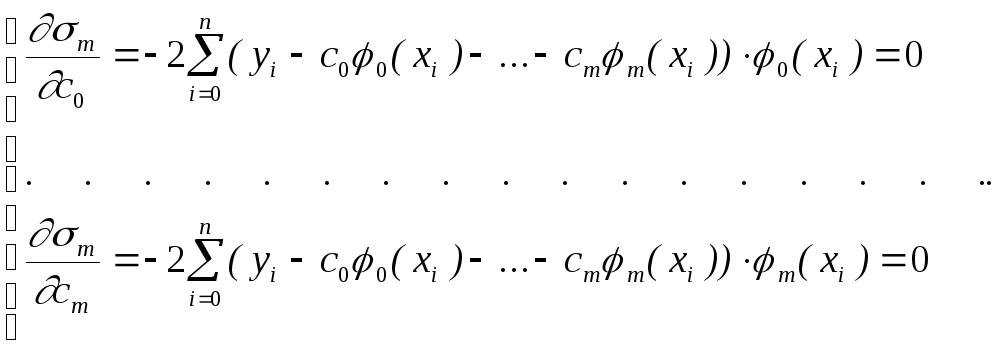(5.13)

Система (5.13) - система линейных уравнений относительно.

Введем определение, чтобы лучше записать (5.13).

Определение. Скалярным произведением функцииfнаgна множестве точекназывается выражение.

Тогда систему (5.13) можно записать в виде:

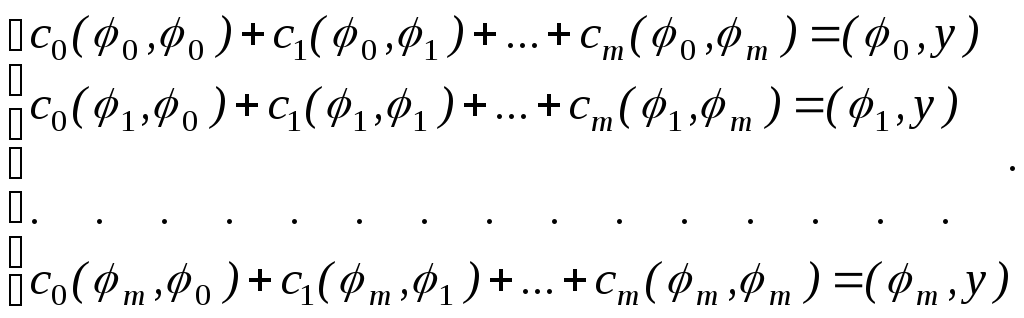(5.13а)

Системы (5.13) и (5.13а) будем называть нормальными системами уравнений.

Решив эти системы, мы найдем коэффициенты , и следовательно, найдем вид аппроксимирующего многочлена. Напомним, что это возможно, если узлы не равноотстоящие и базисные функции линейно не зависимы. Осталось определитьm.

Алгоритм выбора степени ‘’m’’. В случае, когдаm=nмы получим интерполяционный многочлен, поэтомуm<<n. Так же необходимо задать числа₁ и₂,учитывая следующее:

1. ₁ >0 и₂>0 должны быть такими, чтобы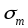находилось между ними;

2. первоначально mвыбирают произвольно, но учитывая условие, чтоm<<n;

3. выбрав m, строят системы (5.13) и (5.13a), решив которые находят;

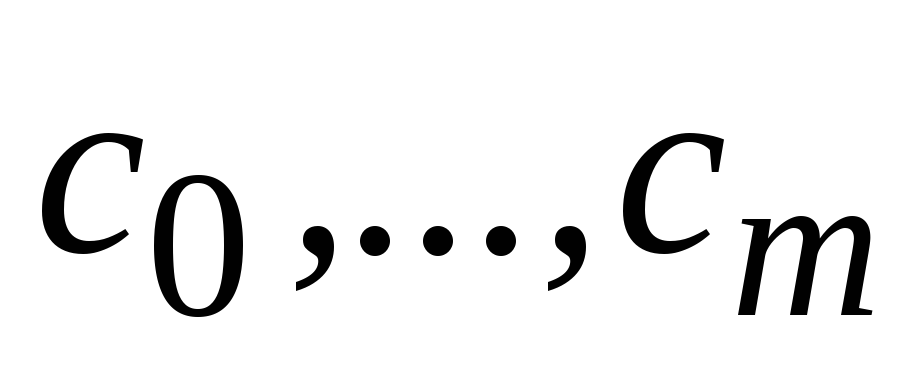4. используя найденные коэффициенты вычисляется 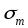и проверяется, попала ли она в промежуток между₁и₂. Если попала, то степень многочлена выбрана правильно, иначе

а) если >₁, то степень необходимо уменьшить хотя бы на единицу;

б) если <₂, то степень необходимо увеличить хотя бы на единицу.

5. затем строить приближающую функцию.

Очень часто для приближения по методу наименьших квадратов используются алгебраические многочлены степени mn, т.е.. Тогда нормальная система (5.13) принимает следующий вид:

(k= 0,1,…,m). (5.14)

Запишем систему (5.14) в развернутом виде в двух наиболее простых случаях m=1 иm=2. В случае многочлена первой степениP₁(x)=c₀+c₁x, нормальная система имеет вид

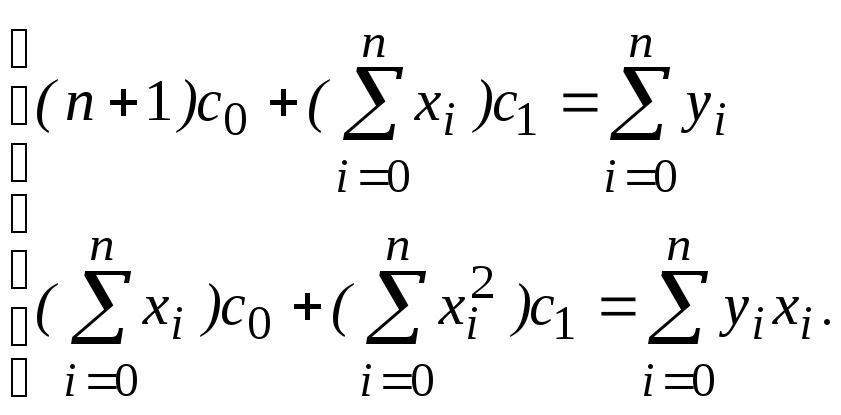(5.15)

Для многочлена второй степени P₂(x)=c₀+c₁x+c₂x², нормальная система имеет вид

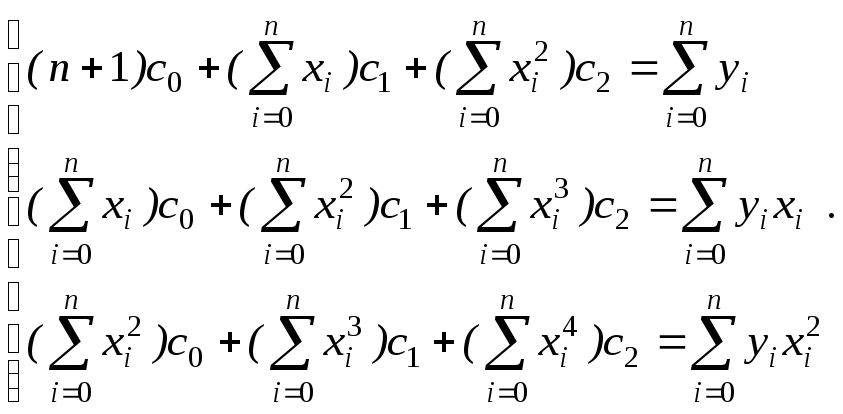(5.16)