Глава1. Метрические пространства

Предисловие

Данное учебно-методическое пособие предназначено студентам-заочникам математического факультета для организации самостоятельной работы и подготовки к зачету и экзамену. В нем содержится теоретический материал раздзела математического анализа “Метрические пространства” и шесть вариантов контрольных работ по тематике разделов математического анализа “Метрические пространства” и “Дифференциальное и интегральное исчисление функции многих переменных”, образец решения нулевого варианта, вопросы к экзамену, список рекомендуемой литературы.

Содержание пособия соответствует программе курса математического анализа.

В пособии использованы распространенные символы математической логики и логические операторы   ,  , 

Для удобства текст, которым начинается и завершается доказательство теорем, показаны значками исоответственно.

§1. Определение и примеры метрических пространств

Известно, что расстояние между двумя точками М₁(х₁,y₁) и М₂(х₂,y₂) плоскости вычисляется по формуле

и имеет свойства:

1) (M₁,M₂) 0; (M₁,M₂) = 0  M₁ = M₂;

2) (M₁,M₂) = (M₂,M₁);

3)(M₁,M₂)  (M₁,M₃) + (M₂,M₃) (неравенство треугольника).

Напомним, что если имеются два непустых множества X и Y, то их декартовым произведением XY называется множества всех упорядоченных пар . В частности X Х обозначается X².

Обобщим понятие расстояния на любое множества с помощью понятия декартового произведения двух множеств: .

Пусть Х – некоторое непустое множества любой природы. Рассмотрим декартовое произведение .

Определение 1.1. Метрикой (расстоянием) на множестве Х называется отображение  декартова произведения Х  Х в множества действительных чисел, удовлетворяющее следующим условиям дляx, y, zX:

1) (x,y)0; (x,y)=0  x = y;

2) (x,y) = (y,x);

3) (x,y)  (x,z) + (y,z) (неравенство треугольника).

Значение функции  в точке (x,y) , т.е. число (x,y), называется расстоянием между точками x и y. Условия 1-3 называются аксиомами метрики.

Определение 1.2. Множества Х с метрикой  на этом множестве, т.е. упорядоченная пара (Х, ), называется метрическом пространством.

Элементы множества Х называются элементами или точками метрического пространства (Х, ).

Пусть дано метрическое пространство (Х, ), пусть МХ, _м(x,y) = (x,y). Очевидно, что и пространство ( М, _м ) в этом случае будет метрическом пространством, поскольку М  М  Х  Х.

Пространство (М, _м) называется подпространством метрического пространства

( Х,  ).

Замечание. Введение понятия расстояния между точками метрического пространства имеет большое значение в математике. Оно позволяет рассмотреть важные вопросы о предельном переходе, непрерывности и дифференцируемости отображений и т.д.

Примеры метрических пространств

Пример 1.1. Пусть R – множества действительных чисел. Для любых чисел x,yR введем функцию (x,y) = х в (1.1). Очевидно, что (1.1) удовлетворяет аксиомам 1 и 2 метрики. Покажем, что функция  удовлетворяет аксиоме 3

 x, y, zR :

(x,y) = х  в= х z + z в х  z+ z  в= (x,z) + (z,y).

Пара (R, ), где  определено равенством (1.1) – метрическое пространство. Его обозначают R или R¹.

Пример 1.2. Множества М=[a,b] с метрикой (x,y) = х вx,y[a,b] обозначают Х = ([a,b], ). Х – подпространство метрического пространства R , поскольку [a,b] R .

Пример 1.3. Множества рациональных чисел Q с метрикой, которая определена формулой (1.1) для всех x, y Q, является метрическом пространством. Пространство Х = (Q,) – подпространство метрического пространства R и обозначается через Q.

Пример 1.4. Обозначим через R^m множества упорядоченных совокупностей m действительных чисел . Элементы множества R^m называются векторами (точками) и обозначаются одной буквой х = (х₁,х₂,…, х_m), y =(y₁,y₂ ,…, y_m). Числа х₁, х₂ ,…, х_m – координаты вектора х. Элементы х и в равны между собой, т.е. х = в, тогда и только тогда, когда х₁ = у₁, х₂ = у₂, …, х_m = у_m.

На множестве R^m введем функцию  (x,y):

x,y R^m. (1.2)

Покажем, что пространство (R^m ,) = R^m, где  определено равенством (1.2), является метрическом пространством.

Функция  удовлетворяет первым двум аксиомам метрики. Для того, чтобы показать, что функция удовлетворяет аксиоме 3, докажем две леммы.

Лемма 1.1. Для любых действительных чисел a_k , b_k, k=1,2,…,m, имеет место неравенство Коши-Буняковского:

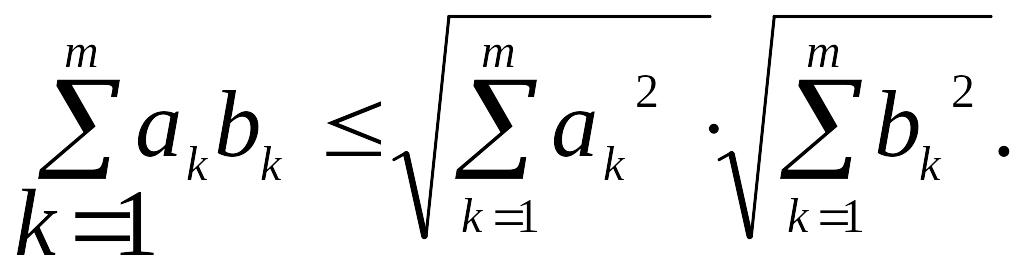(1.3)

Рассмотрим функцию

Поскольку квадратный трехчлен неотрицательный, то дискриминант неположительный:



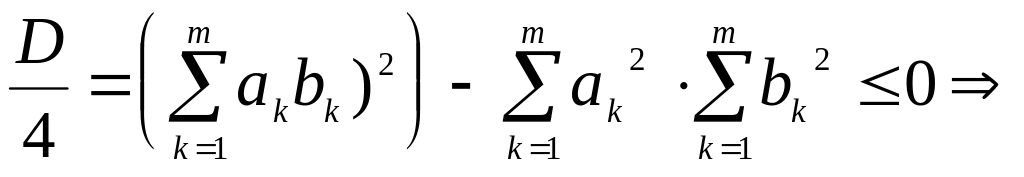
Лемма 1.2. Для любых действительных чисел a_k,b_k , где k = 1,2,…,m имеет место неравенство Минковского:

. (1.4)



 .

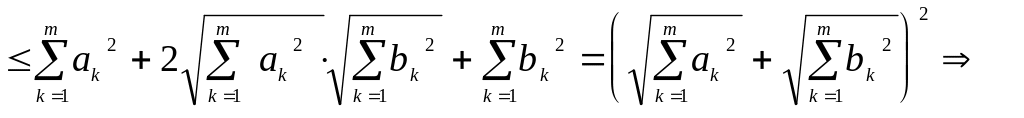
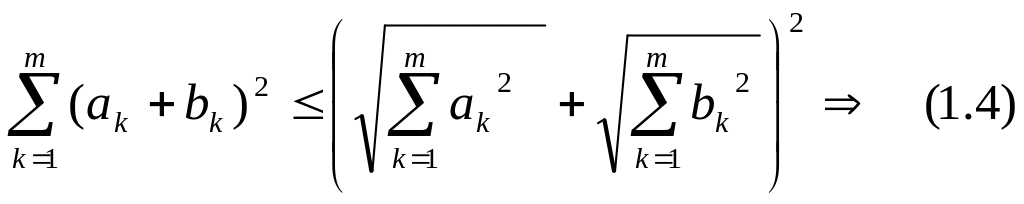Покажем, что для функции (1.2) выполняется аксиома 3 для любых трех точек х = (х₁, х₂, …, х_m), y = (y₁, y₂ , …, y_m), z = (z₁, z₂, …, z_m). Обозначим

a_k = x_k – z_k , b_k = z_k – y_k  a_k + b_k = x_k – z_k + z_k – y_k= x_k – y_k . (1.5)

Подставим в неравенство (1.4) значения из (1.5) и получим



 (x,y)  (x,z) + (z,y). 

Пример 1.5. Рассмотрим также множества R^m , но  зададим с помощью формулы

где х = (х₁,х₂,…, х_m), y = (y₁,y₂ ,…, y_m) – произвольные точки (векторы) пространства R^m. Докажем, что функция (1.6) удовлетворяет аксиомам метрики.

Функция  удовлетворяет первым двум аксиомам метрики . Покажем, что  удовлетворяет аксиоме 3 для любых трех точек

х = (х₁,х₂,…, х_m), y = (y₁,y₂ ,…, y_m), z = (z₁,z₂,…, z_m) пространства R^m.



 (x,y)  (x,z) + (z,y). 

Пример 1.6. Рассмотрим множества С[a,b] всех действительных функций, непрерывных на [a,b]. Для любых двух функций x(t) и y(t) из этого множества положим

(1.7)

Равенство (1.7) – чебышовское расстояние между функциями x(t) и в(t). Покажем, что функция (x,y) – метрика на множестве С[a,b].

Функция  удовлетворяет первым двум аксиомам метрики. Покажем, что  удовлетворяет аксиоме 3.

Пусть x, y, z  С[a,b]. Тогда t [a,b]. Оценим разность

x(t)  y(t)= x(t)  z(t) + z (t)  y(t) x(t)  z(t)+z(t)  y(t)

(x,y)  (x,z) + (z,y). 

Пример 1.7. Рассмотрим l₂ – множества различных числовых последовательностей х₁, х₂, ..., х_n… действительных чисел, для которых сходится ряд . Для любых двух элементов х = х₁, х₂, ... и в = у₁, у₂ ... этого множества определим

. (1.9)

Т.к. ряд сходится, то формула (1.9) определяет функцию для любых х, вl₂. Сходимость этого ряда легко доказать с помощью признака сравнения рядов, если учесть сходимость рядов и и очевидное неравенство .

Функция , заданная формулой (1.9), удовлетворяет аксиомам 1 и 2 (Очевидно). Докажем, что она удовлетворяет и аксиоме 3.

Для любых трех элементов x, y, z множества l₂ имеет место неравенство

 (x,y)  (x,z) + (z,y). 