Основы языка логики высказываний

В логике различают языки логики высказываний и логики предикатов. Язык логики высказываний используется для описания структуры высказываний, рассуждений, предложений. Под высказываниями понимаются простые или сложные абстрактные символические выражения, обозначающие суждения. Простые высказывания, объединенные в сложные с помощью связок «и», «или», «если.., то» и др., называют пропозициональными высказываниями, а логику, с помощью которой описываются такие высказывания, иногда называют пропозициональной логикой, или пропозициональным исчислением. Логика высказываний может быть классической (двузначной) или многозначной.

Язык логики предикатов используется для описания внутренней структуры высказываний. Алфавит языка логики предикатов состоит из следующих символов:

а) а, Ь, с... - постоянные предметные термины;

б) x,y,z...- переменные предметные термины;

в) Р, Q, R ... - предикатные термины (имена свойств);

г) p, q, r ... - пропозициональные термины (имена высказываний);

д) кванторы: - все, - некоторые;

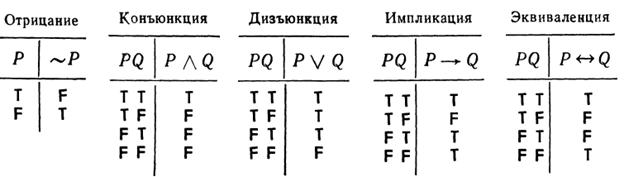
е) , , , - логические союзы, которые соответственно читаются: «и», «или», «если…,то...», «если, и только если, то...» и называются знаком отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности;

ж) технические знаки: , - запятая; () - скобки.

С помощью приведенного алфавита строится формализованная логическая система, называемая исчислением предикатов. Выражения языка логики предикатов называются формулами. Формулы могут быть правильно построенные и неправильно построенные.

Существует особая наука о знаках - семиотика. В этой науке выделяют три раздела - синтаксис, семантику и прагматику, что связано с наличием трех аспектов языка.

Синтаксисом называется раздел семиотики, в котором исследуются отношения между самими знаками (правила построения и преобразования выражений языка и т. д.). В процессе этого исследования отвлекаются от смыслов и значений знаков.

Семантикой называется раздел семиотики, в котором прежде всего исследуются отношения знаков к представляемым ими объектам, а также смыслы знаков, поскольку они являются одним из средств установления связи знаков и их значений.

Прагматика изучает отношение человека к знакам, а также отношения между людьми в процессе знакового общения.

Язык формальной логики позволяет избегать неясности и двусмысленности естественного языка и сводить процесс проверки правильности рассуждений к «вычислению».

Семантическая таблица истинности

Рассмотрим построение таблицы истинности пропозициональной формулы ( A ? B ? C ) ? ( A ? B ) ( см. табл. 9.1). Анализируя таблицу, можно отметить, что большинство информации в ней избыточно. Таблицу можно значительно сократить, пользуясь следующими правилами: для истинности дизъюнкции достаточно истинности одного из членов; для ложности конъюнкции достаточна ложность одного из членов; истина следует из всего что угодно; из лжи следует все что угодно. Сокращенная таблица истинности показана на табл. 9.2 .

Таблица 9.1: Полная таблица истинности

При таком сокращении самым тонким местом является проверка того, что ни один случай не упущен. Можно создавать много способов сокращения таблиц истинности, но в некотором смысле все это будет изобретением велосипеда, поскольку, базируясь на правилах сокращения, голландский логик Бет (Е. W . Beth ) создал в 50-х годах формализм, гарантирующий полноту разбора и выполняющий все прямые сокращения. Он основан на необходимых и достаточных условиях истинности и ложности формул. Начнем с примера для той же формулы.

Таблицы истинности

Под высказыванием мы понимаем повествовательное предложение, которое имеет то свойство, что оно может быть классифицировано либо как истинное, либо как ложное, но не как то и другое вместе. «Истинность» или «ложность» предложения и есть истинностное значение высказывания.

Приписывание истинностных значений может быть сведено в краткие истинностные таблицы, при помощи которых можно приписывать истинностное значение любому высказыванию для всех возможных случаев приписывания истинностных значений составляющим его высказываниям.