Вопрос 16. Шифр с неограниченным ключом

Шифр с неограниченным ключом представляет собой семейство шифров , и объединенных общим способом преобразования множества шифровелечин. Для зашифрования открытого текста длинны l, также для расшифрования криптограммы длины l, шифр с неограниченным ключом использует l-опорный шифр. При этом из множества выбираем ключом в соответствии с распределением P( ).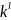

Может возникнуть вопрос, почему вместо семейства моделей не рассматривают оду модель с множеством открытых текстов и с множеством ключей 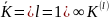и множество шифротекстов . Такой подход обладает следующим существенным недостатком, дело в том что при этом не всякий открытый текст можно зашифровать на любом ключе. В самом деле ключ 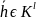можно применять лишь к открытому тексту 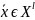, поэтому мы не можем рассматривать правила зашифрования как отображения . По этому будем исходить из того что для любой модели шифра типа (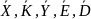 ) правила зашифрования являются отображения следующего вида .

Шифр с НЕ ограниченным ключом – ключами шифра служат всевозможные ключевые потоки. Шифр с неограниченным ключом полностью определяется своим действием на мн-вешифровеличин и рандомизаторов.

Ключевой поток может получаться случайным образом, например, с помощью рандомизатора типа игровой рулетки. Такой шифр мы будем называть шифром с неограниченным ключом. Ключами шифра служат всевозможные ключевые потоки. Шифр с неограниченным ключом полностью определяется своим действием на множестве шифрвеличин и рандомизатором.

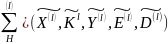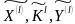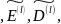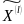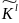Пусть - совокупность случайных величин , множеств правил зашифрования и расшифрования для которой выполняются условия P{ = } > 0, P{ = } > 0. l -й опорный шифр шифра

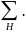
Тогда шифром замены с неограниченным ключом назовем семейство 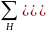l N). Шифр с неограниченным ключом представляет собой семейство шифров 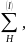действующих на множествах 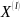открытых текстов, l ∈ Ν , и объединенных общим способом преобразования множества шифрвеличин. Для зашифрования открытого текста длины l (так же как и для расшифрования криптограммы длины l ) шифр с неограниченным ключом использует l -й опорный шифр. При этом из множества с помощью некоторого рандомизатора случайно выбирается ключ в соответствии с априорным распределением P( ).

Вопрос 17. Модель шифра с ограниченным ключом.

Исходными предпосылками построения такого шифра служит опорный шифр сигма, конечное множество ключей-К, и множество правил зашифрования { K,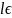 N }, в определении действия 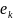. Также как и для шифра с неограниченным ключом используется ,

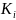
, i=1,l , где по прежнему К={0,1,…,n-1} множество номеров простых замен входящих в опорный шифр.

Отличие шифра с неограниченным ключом состоит в следующем: для шифра с ограниченным ключом, ключевой поток вычисляется по выбранному ключу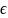 k K.

Определение 4. Пусть C:K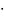 N--> – произвольное отображение, такое что для любы k K и n N, i=1,l

Такое что ψ (k,l)=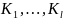 причем множество отображений { ψ (k,l), k K}=K , назовем последовательность ….., а само отображение кси- генератором ключевого потока. Причем в этом определении ключевой поток однозначно определяется ключом k K и числом l.

Введем последовательность моделей, ,l N при этом будем исходить из некоторых априорных распределений ключей Р(к) и открытых ключей P( ), l N . Существенное отличие от аналогичной модели для шифра с неограниченным ключом состоит в том что, в качестве множества возможных ключевых потоком длины l, которое задается следующим образом . Пусть 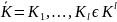тогда 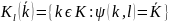. Введем следующее распределение P( 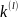), введем распределение .

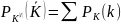Определение 5. Пусть имеется математическая модель 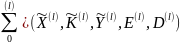, где совокупность случайных величин 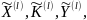правила зашифрования и расшифрования 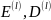, распределение P( ), определяется нашей формулой и выполняется следующее условие P{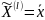 }>0. Для всех тогда шифром ….

Заметим что для всех l 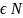образует разбиение К на классы эквивалентных ключей, прождающих одинаковые ключевые потоки длины l. Поэтому лучше выбирать дляшифрования открытого текста длины l не столько ключ k K сколько порождаемый этим ключом ключевой поток.

Криптографические свойства шифра с ограниченным ключом определяется в первую очередь свойствами генератора ключевого потока.

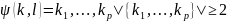Например если: где все k K, то получаем слабый шифр простой замены. Если генератор выдаёт нам следующую последовательность ,то мы получаем переодическую последовательность. То получаем более стойкий шифр, например Виженера.