Уравнения максимальной работы (уравнения Гиббса-Гельмгольца).

Свойства функций F и G дают возможность установить связь между максимальной работой процесса, протекающего равновесно, и теплотой того же процесса, но протекающего неравновесно.

= – S , F = U – TS, F = U + T

Запишем это уравнение для двух состояний системы:

F₁ = U₁ + T , F₂ = U₂ + T

F₁ – F₂ = U₁ – U₂ + T (F₁ – F₂)_V = – F

A_max = + T (1)

Видно: зная A_max (или изменение изохорного потенциала) и зависимость ее от Т, можно вычислить теплоту процесса (т.е. изменение внутренней энергии).

Если же известна Q процесса, то для расчета A_max необходимо интегрировать уравнение (1), причем появляется постоянная интегрирования, для определения которой необходимы дополнительные сведения.

Уравнение (1) – уравнение максимальной работы (уравнение Гиббса-Гельмгольца) – может быть записано и в форме:

F = U + T (2)

Другие варианты уравнения Гиббса-Гельмгольца:

= – S , G = H – TS , G = H + T

G₁ = H₁ + T , G₂ = H₂ + T

G₁ – G₂ = H₁ – H₂ + T (G₁ – G₂)_P

A_max = + T (3)

G = H + T (4)

U = Q_V и H = Q_P справедливы, если в 1-м случае не совершается никакая работа (А = 0), а во 2-м случае совершается только работа расширения (А = 0). Поэтому в уравнениях (1) и (3) теплоты и относятся не к процессам, которым соответствуют работы А или А, а к процессам, протекающим между теми же начальным и конечным состояниями, но без совершения работы (для Q_V) или с совершением только работы расширения (для Q_P), т.е. в неравновесных условиях. Теплоты же равновесного процесса, равные ТS, выражаются последними членами уравнений (1) и (3).

Исходя из вышеизложенного, эти уравнения можно записать так:

– F = A_max = – Q_{V, неравн} + Q_{V, равн}

– G = A_max = – Q_{P, неравн} + Q_{P, равн}

Статистический характер II закона термодинамики.

Термодинамический метод неприменим к системам, состоящим из малого числа молекул (единицы, десятки, сотни). Это связано с тем, что в таких системах исчезает различие между теплотой и работой. Одновременно исчезает однозначность направления процесса, устанавливаемая вторым законом термодинамики. Категорическое утверждение о невозможности одного из направлений процесса заменяется оценкой относительной вероятности обоих противоположных направлений. Для очень малого числа молекул оба направления процесса становятся равноценными. Чисто механическое движение отдельных молекул обратимо и преимущественного направления не имеет.

В отличие от I закона термодинамики, который является абсолютным, II закон термодинамики имеет статистический характер, он справедлив лишь для систем, имеющих большое число частиц. Ограничения перевода теплоты в работу, которые устанавливаются вторым законом термодинамики, в противоположность неограниченному переводу работы в теплоту, связаны со стремлением системы, содержащей большое число частиц, к молекулярному беспорядку, мерой которого служит энтропия.

Работа характеризуется упорядоченным коллективным движением частиц в одном направлении; теплота связана с хаотическим молекулярным движением. Поэтому выясняется самопроизвольный характер перехода работы в теплоту, как перехода молекулярной системы к более вероятному состоянию, которому отвечает большая степень молекулярного беспорядка.

Причиной стремления к равновесию является переход молекулярной системы от менее вероятного состояния к более вероятному состоянию большего молекулярного беспорядка; при этом возрастает энтропия. Связь между S и вероятностью состояния системы можно установить таким образом: любое термодинамическое макросостояние системы может быть осуществлено различными микросостояниями. Число микросостояний, с помощью которых можно осуществить данное макросостояние системы, называется термодинамической вероятностью W.

Число микросостояний можно рассчитать по формуле:

W =

N – общее число молекул, распределенных либо по k отделениям, либо по k уровням, либо по скоростям и т.д.;

N₁ – число молекул в 1-м отделении;

N₂ – число молекул во 2-м отделении …

Рассмотрим, как меняется W по мере протекания процесса. Самопроизвольный процесс сопровождается возрастанием S; при этом резко возрастает также W. Следовательно, S и W должны быть связаны друг с другом:

S = S (W)

Надо учесть аддитивность S: S = S₁ + S₂

Для W: W = W₁  W₂

(вероятность события равна произведению вероятностей отдельных независимых событий).

Если равновесная система с вероятностью W и энтропией S состоит из двух частей с вероятностями W₁ и W₂ и энтропиями S₁ и S₂ , то можно записать:

S₁ = f (W₁) , S₂ = f (W₂)

S = f (W) = f (W₁W₂) , S₁ + S₂ = f (W₁) + f (W₂)

f (W) = f (W₁W₂) = f (W₁) + f (W₂)

Для системы из многих частей:

f (W) = f (W₁W₂ … W_k) = f (W₁) + f (W₂) + … + f (W_k)

Решением этого уравнения является уравнение Больцмана:

S = k ln W

k – постоянная Больцмана; k = R / N_A

Рассмотрим процесс изотермического расширения 1 кмоля идеального газа.

S = = = R ln = kN ln W1 = – вероятность нахождения одной молекулы в объеме V1 W1 = – вероятность нахождения одной молекулы в объеме V2

Для N молекул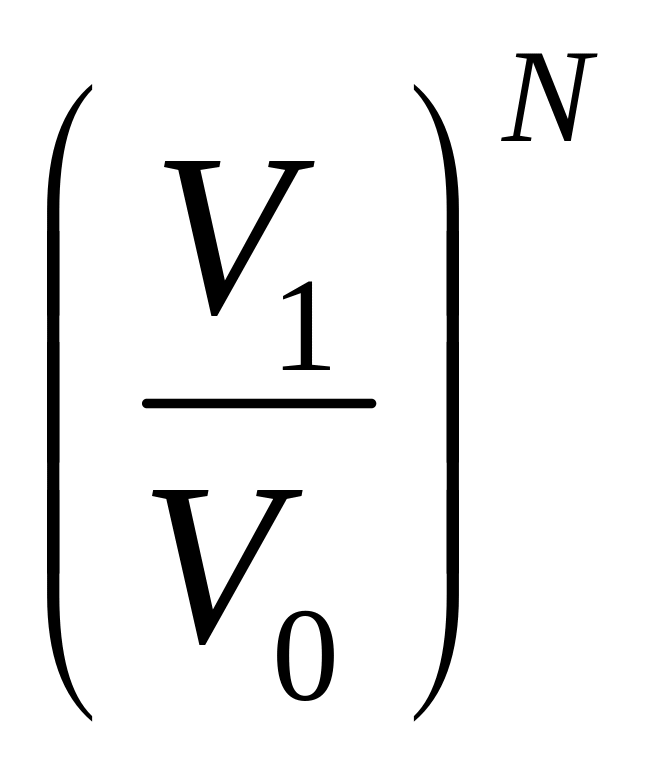: W_N = , W_N =

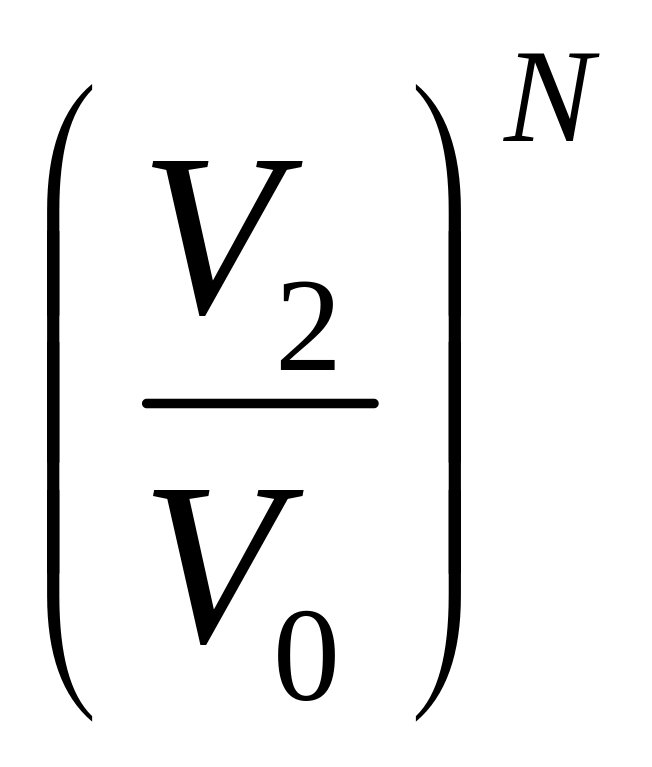
= , ln = N ln , S = k ln

S₂ – S₁ = k ln W_N – k ln W_N , S = k ln W + const

сonst = 0 – постулат Больцмана  S = k ln W

Это соотношение вскрывает статистический характер II закона термодинамики. Условие возрастания S в изолированной системе не обязательно, а вероятно. Возможны самопроизвольные отрицательные процессы, сопровождающиеся уменьшением S в изолированной системе, например, флуктуации плотности (не только возможны, но и повсеместно осуществляются). Значительные отклонения от средних величин в больших системах имеют исчезающе малую вероятность, но в принципе они также возможны.

Установление статистического характера II закона термодинамики является великой заслугой Больцмана, объяснившего таким образом противоречие между обратимостью механического движения и необратимостью и направленностью реальных физических и химических процессов. Эта направленность является следствием молекулярного строения материального мира.

В работах Больцмана, Смолуховского и др. ученых показан статистический характер II закона термодинамики и количественно изучены наблюдаемые отклонения от этого закона. Этими работами окончательно показана несостоятельность антинаучной идеи тепловой смерти вселенной, высказанной Клаузиусом.

Клаузиус неправильно толковал II закон термодинамики (одним из творцов которого он был), как абсолютный закон природы. Незаконно распространяя свой постулат на вселенную, которую он уподоблял изолированной системе, и на неограниченный промежуток времени, Клаузиус дал второму закону термодинамики следующую формулировку: энтропия вселенной стремится к максимуму.

Из этого положения вытекают два вывода:

1. Через достаточно большой промежуток времени вселенная приблизится к такому состоянию, что ее энтропия будет близка к максимальной величине; состояние вселенной будет близко к равновесному и все процессы угаснут – останутся равномерно распределенные в пространстве материя и энергия. Дальнейшая эволюция вселенной прекратится, наступит «тепловая смерть вселенной».

2. Т.к. в настоящее время вселенная далека от «тепловой смерти», хотя и движется только в направлении к ней, то, следовательно, вселенная имела начало, она возникла в противоречии со II законом термодинамики (имеющим абсолютное значение) в результате какого-то творческого акта, не подчиняющегося законам природы.

Выводы Клаузиуса о тепловой смерти вселенной незакономерны, т.к. термодинамические свойства конечной изолированной системы распространялись им на вселенную, безграничную в пространстве и времени. Работы Больцмана и др. ученых, установивших ограниченный статистический характер II закона термодинамики, показали возможность и необходимость наличия во вселенной любых по величине отклонений от требований второго закона для равновесных систем. Само представление о движении вселенной (как целого) к равновесию незакономерно.

Лекция 8

Термодинамические потенциалы идеальных и реальных газов. Летучесть и методы ее расчета.

1. Внутренняя энергия 1 моля идеального газа, зависящая только от Т, выражается уравнением: dU = C_V dT , U = U_o +

2. Энтальпия:

H = U + PV = U_o + + RT = U_o + = U_o +

3. Энтропия:

S = C_V ln T + R ln V + S_o , S = C_P ln T  R ln P + S_o

4. dF = – PdV – SdT , dG = VdP – SdT

Пусть T = const:

dF = – PdV = – dV , dG = VdP = dP

F = – RT ln V + F(T) , G = RT ln P + G(T)

(т.к. интегрирование проведено при T = const, то постоянные интегрирования – функции Т).

Для реальных газов Льюис предложил формальный прием, который позволяет связать найденные опытным путем свойства реального газа (отклонения его от идеального состояния) с его термодинамическими параметрами и изучать таким путем термодинамические закономерности в реальных газовых системах. При этом сохраняются те же простые формулы, что и для идеальных газов. По методу Льюиса вводится новая функция f – термодинамическая летучесть, обобщенная летучесть; кратко – летучесть,

фугитивность. f подставляется в термодинамические уравнения вместо Р.

G = RT ln f + G(T) (1)

При этом вводится условие: lim = 1 при Р  0 (2)

Т.о., метод Льюиса – это математический прием, который состоит в введении новой функции f, промежуточной между параметрами состояния газа Р и Т, с одной стороны, и G – с другой стороны.

G = G₂ – G₁ = RT ln f₂ / f₁ при T = const

Чтобы вычислить G для процессов с реальным газом, нужно знать зависимость f от Р и Т. Уравнение (1) и условие (2) – это основа для вычисления f.

Продифференцируем уравнение (1) по Р при Т = const:

= RT

Учитывая, что = V, получаем: V = RT

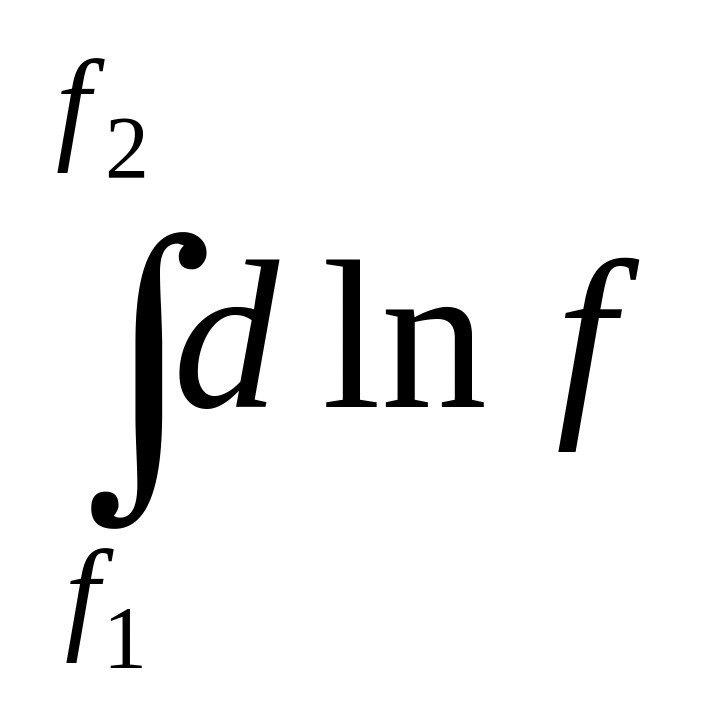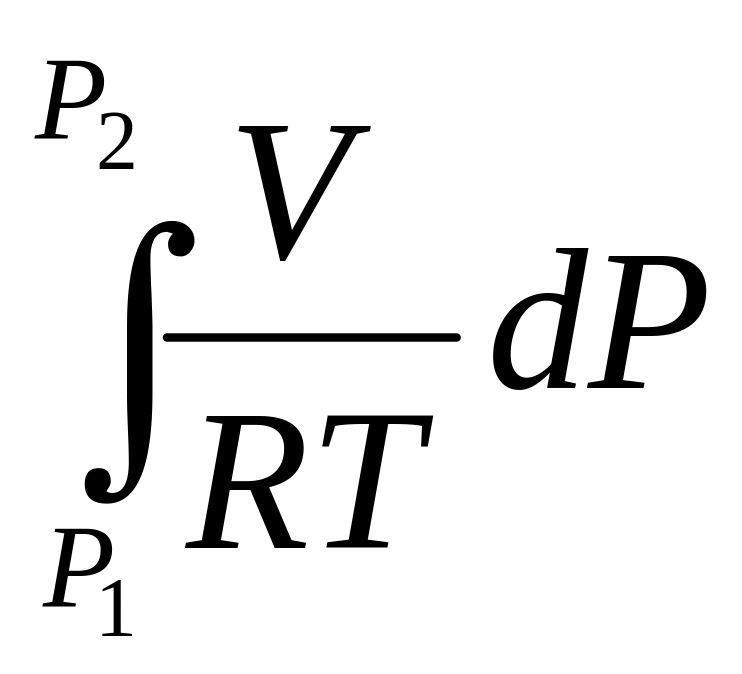= , ln =

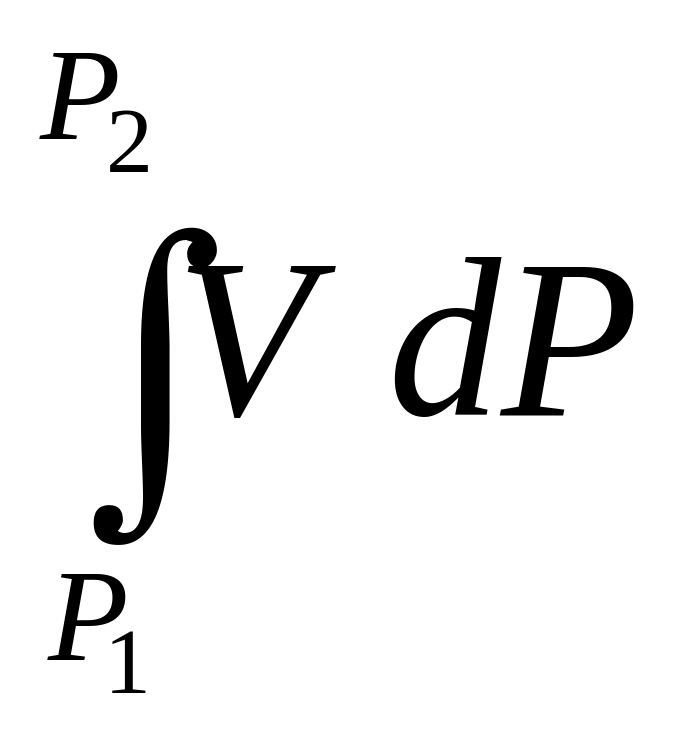
Надо знать зависимость V от Р. Наиболее точный способ заключается в графическом нахождении интеграла этого уравнения. Для этого по экспериментальным значениям V, который занимает 1 моль газа при разных Р, строят кривую зависимости V от Р. Интеграл равен площади под соответствующей частью кривой.

Имея опытные данные V = V(P), вычисляют так называемую объемную поправку реального газа , определяемую по уравнению:

V = –  ,   0 при не слишком высоких Р

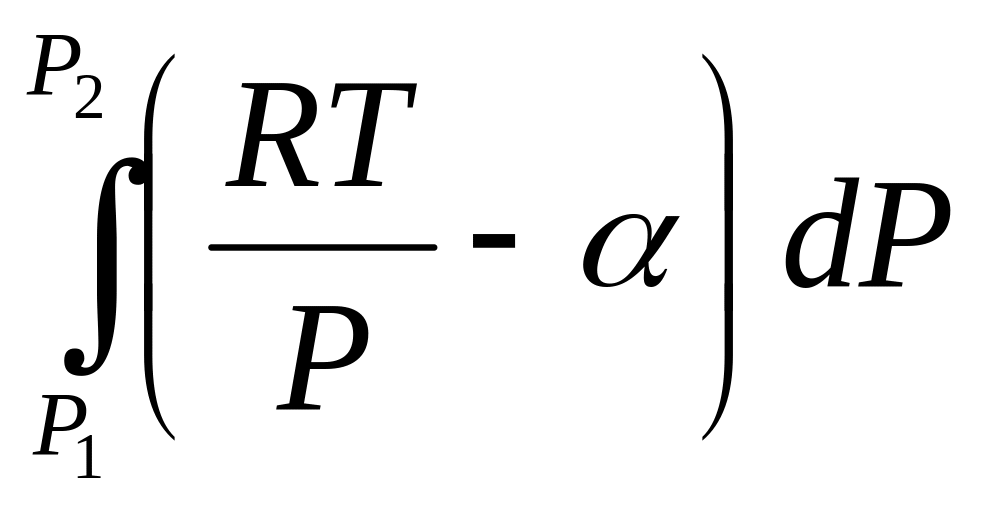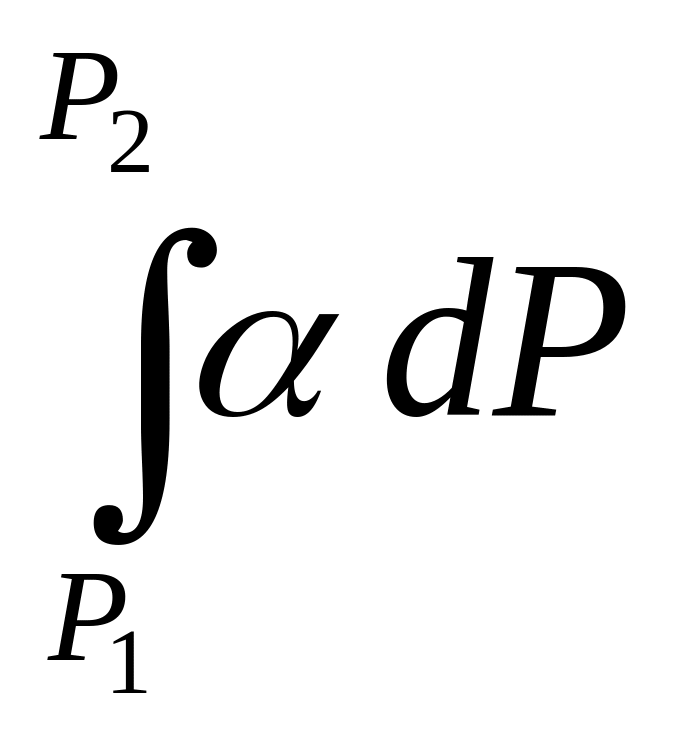ln = = ln – , надо знать  =  (Р).

ln f₂ – ln f₁ = ln P₂ – ln P₁ –

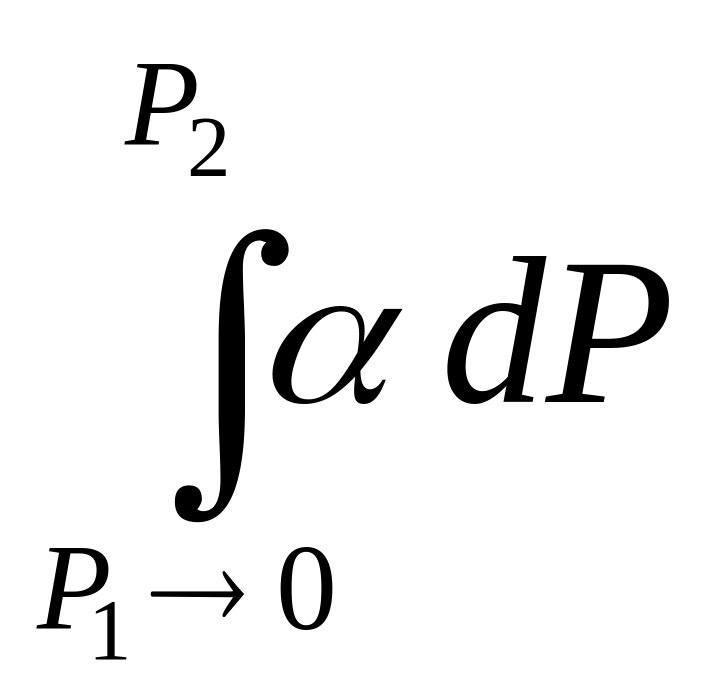
Пусть нижний предел интегрирования Р₁ очень мал, так чтобы f₁ = P₁ :

ln f = ln P –

ln = – , = exp (– )

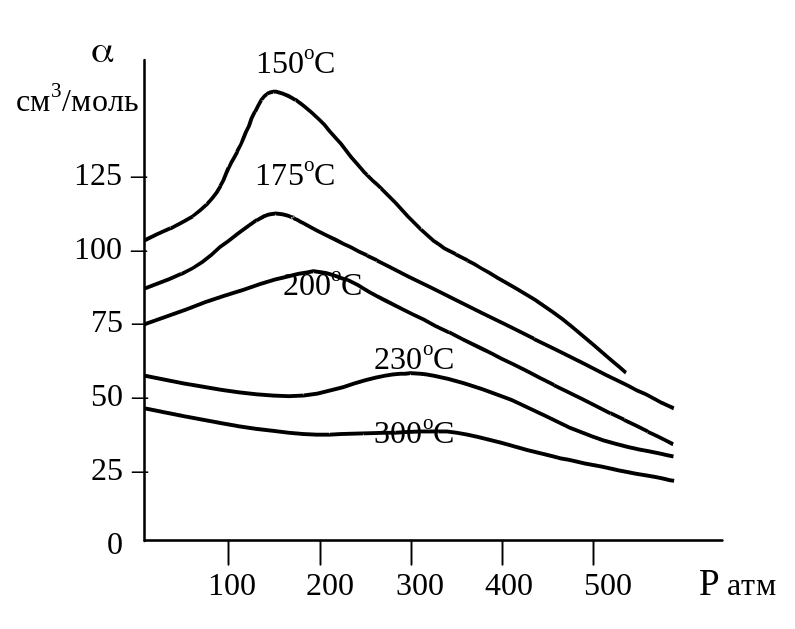
 = называется коэффициентом активности или коэффициентом летучести газа. Изобразим зависимость величины  = – V от Р, характерную для

многих реальных газов при обычной Т: 1. При достаточно высоких Т  мало изменяется с ростом Р в широком интервале Р, начиная от малых Р. 2. Площадь под кривой от Р = 0 соответствует величине интеграла в вышеприведенном уравнении. 3. При повышении Р  для многих газов меняет знак. Поэтому летучесть многих реальных газов сначала меньше Р, потом равна Р, а затем больше Р (при больших Р).

Если Т – высокие, Р – невысокие,  = const, тогда:

ln f = ln P – ,  = = exp (– )