Вопрос 27. Производственная функция. Закон убывающей эффективности.

Производственная функция - это функция, независимая переменная которой принимает значения объемов затрачиваемого или используемого ресурса (фактора производства), а зависимая переменная - значения объемов выпускаемой продукции у=f(x).

В формуле х (х > 0) и у (у > 0) - числовые величины, т.е. у = f(x) есть функция одной переменной х. В связи с этим производственная функция (ПФ)/называется одноресурсной или однофакторной ПФ, ее область определения - множество неотрицательных действительных чисел (т.е. х>0). Запись у =f(x) означает, что если ресурс затрачивается или используется в количестве х единиц, то продукция выпускается в количестве у = f(х) единиц. Символ f -знак функции - является характеристикой производственной системы, преобразующей ресурс в выпуск. Символ f связывает между собой независимую переменную х с зависимой переменной у. В микроэкономической теории принято считать, что у - это максимально возможный объем выпуска продукции, если ресурс затрачивается или используется в количестве х единиц. В макроэкономике такое понимание не совсем корректно: возможно, при другом распределении ресурсов между структурными единицами экономики выпуск мог бы быть и большим. В этом случае ПФ - это статистически устойчивая связь между затратами ресурса и выпуском. Более правильной является символика у =f(x, а), где а - вектор параметров ПФ.

В озьмем ПФ f в виде f{x) = ах^b, где х - величина затрачиваемого ресурса (например, рабочего времени), f(х) - объем выпускаемой продукции (например, число готовых к отправке холодильников). Величины а и b - параметры ПФ. Здесь а и b -положительные числа и число b < 1, вектор параметров есть двумерный вектор (а, b).

График производственной функции у = ах^b изображен на рис. На графике видно, что с ростом величины затрачиваемого ресурса х объем выпуска у растет, однако при этом каждая дополнительная единица ресурса дает все меньший прирост объема у выпускаемой продукции. Отмеченное обстоятельство (рост объема у и уменьшение прироста объема у с ростом величины х) отражает фундаментальное положение экономической теории (хорошо подтверждаемое практикой), называемое законом убывающей эффективности. ПФ у = ах^b является типичным представителем широкого класса однофакторных ПФ.

ПФ могут иметь разные области использования. Принцип "затраты - выпуск" может быть реализован как на микро-, так и на макроэкономическом уровне. ПФ , рассмотренная выше, может быть использована для описания взаимосвязи между величиной затрачиваемого или используемого ресурса х в течение года на отдельном предприятии (фирме) и годовым выпуском продукции у этого предприятия (фирмы). В роли производственной системы здесь выступает отдельное предприятие (фирма) - имеем микроэкономическую ПФ (МИПФ). На микроэкономическом уровне в роли производственной системы может выступать также отрасль, межотраслевой производственный комплекс. МИПФ строятся и используются в основном для решения задач анализа и планирования, а также задач прогнозирования.

ПФ может быть использована для описания взаимосвязи между годовыми затратами труда в масштабе региона или страны в целом и годовым конечным выпуском продукции (или доходом) этого региона или страны в целом. Здесь в роли производственной системы выступает регион или страна в целом (точнее хозяйственная система региона или страны) - имеем макроэкономический уровень и макроэкономическую ПФ (МАПФ). МАПФ строятся и активно используются для решения всех трех типов задач (анализа, планирования и прогнозирования).

Производственная функция нескольких переменных - это функция, независимые переменные x_v ... ,х_п которой принимают значения объемов затрачиваемых или используемых ресурсов (число переменных п равно числу ресурсов), а значение функции имеет смысл величин объемов выпуска:

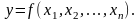
В формуле у (у >0) - скалярная, f- векторная величина, х₁ ..., х_п - координаты вектора х, т.е. f(х₁ , ... , х_п) есть числовая функция нескольких (многих) переменных х,,..., х_п. В связи с этим ПФ f(x₁, ... , х_п) называют многоресурсной или многофакторной ПФ.

ПФ называется динамической, если:

1) время t фигурирует в качестве самостоятельной переменной величины (как бы самостоятельного фактора производства), влияющего на объем выпускаемой продукции;

2) параметры ПФ и ее характеристика зависят от времени t.

Формальные свойства производственных функций

Производственная функция как формальная конструкция определена в неотрицательном октанте двумерной плоскости, т.е. определена при х₁ > 0, х₂ > 0. ПФ должна удовлетворять ряду (для каждой конкретной ПФ - своему) свойств:

Свойство 1 означает, что без ресурсов нет выпуска, следующее свойство означает, что при отсутствии хотя бы одного из ресурсов нет выпуска.

Свойство 2 означает, что с ростом затрат хотя бы одного ресурса объем выпуска растет. Свойство 2" (первая частная производная ПФ положительна) означает, что с ростом затрат одного ресурса при неизменном количестве другого ресурса объем выпуска растет.

Свойство 3 (вторая частная производная ПФ неположительна) означает, что с ростом затрат одного ресурса при неизменном количестве другого ресурса величина прироста выпуска на каждую дополнительную единицу j-го ресурса не растет (закон убывающей эффективности).

Свойство 4 означает, что ПФ является однородной функцией (ОФ) степени р > 0.

Применение производственных функций не ограничивается выявлением зависимости затраты-выпуск. Различные приемы математического аппарата позволяют использовать их для вычисления численных характеристик производства, анализа эффективности изменения масштаба производства и технологического прогресса, исследования эластичности производственных факторов, рационального ведения хозяйства, оптимального планирования и прогнозирования вариантов развития фирмы и др.

Поэтому очень важно, чтобы производственная функция объективно отражала моделируемую действительность, т.е. чтобы она удовлетворяла содержательно-логическим и экономическим требованиям. Основные из них следующие:

• в число аргументов производственной функции должны быть включены все существенные для данного процесса факторы;

• все величины должны иметь отчетливый экономический смысл;

• все экономические величины, входящие в производственную функцию, должны быть измеримы;

• выпуск продукции без затрат невозможен;

• если величина какого-либо ресурса ограничена, то выпуск не может расти бесконечно;

• увеличение затрат не может привести к уменьшению выпуска.

Упрощенные примеры производственных функций - это линейная производственная функция: двухфакторн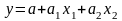ая , и многофакторная .

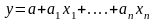Первый успешный опыт построения производственной функции, как уравнения регрессии на базе статистических данных, был получен американскими учеными - математиком Д. Коббом и экономистом П. Дугласом в 1928 году. Предложенная ими функция изначально имела вид:

где Y - объем выпуска, K - величина производственных фондов (капитал), L - затраты труда, - числовые параметры (масштабное число и показатель эластичности). Благодаря своей простоте и рациональности, эта функция широко применяется до сих пор и получила дальнейшие обобщения в различных направлениях. Функцию Кобба-Дугласа иногда мы будем записывать в виде

Легко проверить, что и

Кроме того, функция линейно-однородна:

.

Для многофакторного производства функция Кобба-Дугласа имеет вид:

Для учета технического прогресса в функцию Кобба-Дугласа вводят специальный множитель (технического прогресса) , где t - параметр времени, - постоянное число, характеризующее темп развития. В результате функция принимает "динамический" вид:

где не обязательно .

Рассмотрим ПФ Кобба-Дугласа. 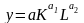. Где Разделим обе части функции на L.

.

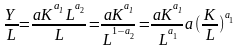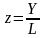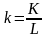Полученные дроби и называются производительностью труда и капиталловооруженностью труда.