5.3. Дополнительные уравнения и выражения

Относительный подогрев

(6)

Изменение давления торможения

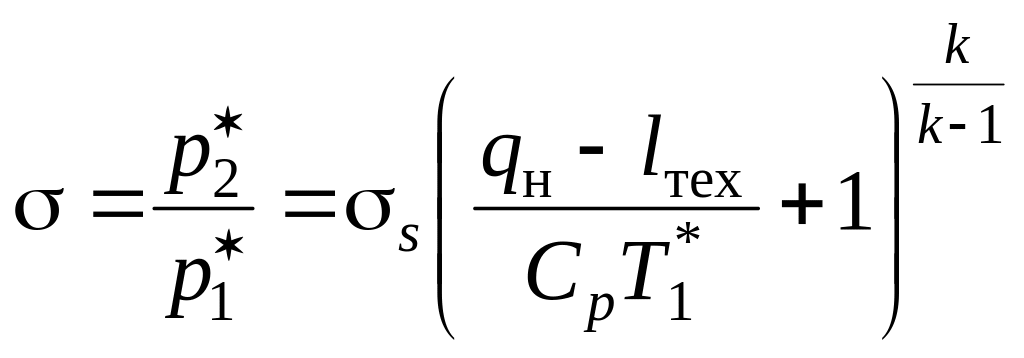(7)

Потери давления торможения (коэффициент потерь эксергии)

(8)

Изменение давления в изоэнтропическом процессе

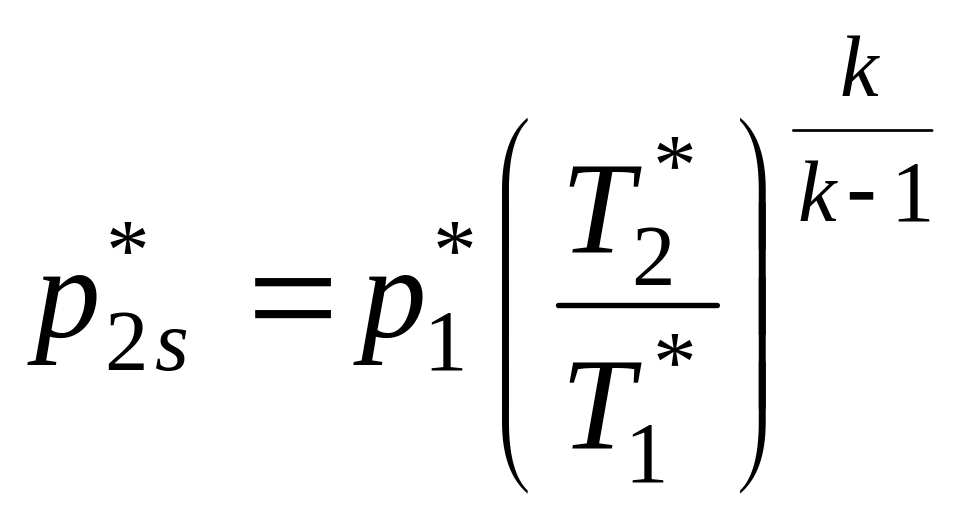(9)

Уравнение для качественной оценки изменения давления торможения

(10)

Уравнение закона обращения воздействий

(11)

Линейные потери давления торможения

(12)

Коэффициенты трения

при Re<Re_кр ζ_тр=64/Re (13)

при Re>Re_кр (14)

Изменение эксергии

[Дж/кг] (15)

Потери эксергии

[Дж/кг] (16)

Граничное условие по давлению

р_сист = р_н при М < 1 (17)

5.4. Задачи по теме 5

Задача 1

На входе в цилиндрический канал с площадью поперечного сечения F заданы давление р₁, температура Т₁ и скорость W₁ газа (значения этих параметров приведены в табл. 5) Определить все параметры (статические и торможения) потока на выходе из канала, изменение давления торможения σ, потери давления торможения σ_s, если при подводе тепла к газу его температура на выходе из трубы стала равной Т₂^* (см. табл. 5). Рабочим телом является воздух с газовой постоянной R = 287 Дж/кгК и показателем изоэнтропы k = 1,4. Трением пренебречь.

Задача 2

До какой температуры Т₂^* необходимо подогреть газ в цилиндрическом канале с площадью F, во входном сечении которого параметры газа равны параметрам газа задачи 1, чтобы на выходе из канала получить скорость звука. Определить все параметры на выходе из канала и сопоставить результаты этой задачи с результатами задачи 1.

Задача 3

В цилиндрическом канале с площадью F, во входном сечении которого параметры газа равны параметрам газа в выходном сечении канала задачи 2, отводится тепло. Какое количество тепла необходимо отвести от газа, чтобы на выходе из канала получить число Маха М = 2. Определить все параметры газа в этом сечении канала.

Задача 4

Определить длину цилиндрической трубы с трением (без подвода тепла), на выходе из которой скорость газа равна скорости звука, а на входе все параметры газа имеют такие же значения, как в задаче 1.

Задача 5

Определить длину цилиндрической трубы с трением (без подвода тепла), параметры газа на входе в которую такие же, как в задаче 1, а статическое давление на выходе равно значению статического давления в задаче 2. Определить все параметры на выходе из трубы. Сравнить результаты задач 4 и 5.

Задача 6

Решить задачу 1 с учетом трения, полагая скорость на выходе из трубы равной скорости звука. Определить длину трубы, сравнить результаты с результатами задачи 4.

Таблица 5