19. Уравнение колмагорова для процесса гибели-размножения

 В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения. Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.  Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.    Рис. 4  Рассмотрим упорядоченное множество состояний системы S₀, S₁, S₂, …, S_k. Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния S_kвозможны переходы только либо в состояние S_k-1, либо в состояние S_k+1. (При анализе численности популяций считают, что состояние S_k соответствует численности популяции, равной k, и переход системы из состояния S_k в состояние S_k+1 происходит при рождении одного члена популяции, а переход в состояние S_k-1, — при гибели одного члена популяции).  Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями l_{k, k+1} или l_{k+1, k}.  По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).  В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния S₀                                                                         (12)  для состояния S₁ – ( l₁₂+l ₁₀)p₁=l₀₁ p₀+ l₂₁p₂, которое с учетом (12) приводится к виду                                                                                            (13)  Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:                                                                                           (14)  к которой добавляется нормировочное условие                                                                             (15)     Решая систему (14), (15), можно получить                                     (16)                       (17)  Легко заметить, что в формулах (17) для p₁, p₂, …, p_n коэффициенты при p₀ есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния S_k (k=1, 2, …, n), а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния S_k. 

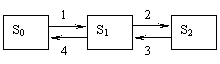
20. Вывод соотношений для Процесса гибели – размножения.

21.Канонический метод построения алгоритмов моделирования смо

В одноканальную СМО поступают случ поток заявок с азаднным законом распределения интервалов м/у заявками. Время распределения также случайно. Если канал занят то заявка покидает систему.

Опр-ть вер-ть отказа, ср время занятости канала.

Процесс фукнционирования наблюдают на [0,T]. Т выбирается из точности и достоверности оценок.

P1 – логический оператор, сравнивающий t_j и Т: t_j < T; t_j – время получения заявки.

М- число реализаций процессов наблюдения. М задают из условия стабильности, точности, достоверности основных хар-к

P3: m<M (сравнение)

P2; t_j-1^осв < t_j - завявка обслуживается , если это рарушается – заявка получает отказ.

Арифметические операторы:

А0 – вычисление случайного времени прихода j-ой заявки по заданному закону распределения.

А1 – считает число реализаций m

A2 – статистическая обработка рез-тов и вывод их

А3 – вычисляет случайное время освобождения канала от предыдущей заявки.

А3: t_j + [тау]_j ; [тау]_{j –} время обслуживания j-ой заявки ; t_j - время прихода

А4 – подсчет количества обслуженных заявок

А5 – подсчет количества необслуженных заявок

А6 – подсчет среднего времени занятости системы

Z – пустой оператор. Когда вычисление не имеет смысла, а программа представляет собой дерево, но не все ветки будут правильны.

End – оператор окончания.

Характеристическая таблица.

Число строк = сочитание логических операторов,т.е. 8(??)

Число столбцов = 3 (???) столбца логич + (???)последовать арифметических операций

N0	P1	N2	P2	N3	P3	N4
A0	0	А1	0	Z	0	A2, End
A0	0	А1	0	Z	1	A0
A0	0	А1	1	Z	0	A2, End
A0	0	А1	1	Z	1	A0
A0	1	А3	0	A5, A0	0	Z
A0	1	А3	0	A5, A0	1	Z
A0	1	А3	1	A4, A6, A0	0	Z
A0	1	А3	1	A4, A6, A0	1	Z