15. Теорема Котельникова. Дискретизация сигналов.
Теорема Котельникова. Дискретизация сигналов.
Теорема Котельникова (теорема отсчетов), определяет условия, при которых непрерывный сигнал, дискретизированный по временной (или пространственной) переменной, может быть восстановлен по своим отсчетам без потери какой-либо информации о нем.
Согласно теореме
Котельникова, если Т такой интервал
дискретизации, что
и выполняются следующие условия:
1) функция x(t)
определена для всех значений времени
;
2) существует преобразование Фурье X(f) функции x(t);
3) функция X(f) ограничена, т.е. |X(f)|=0 при |f|>Fn,
тогда функция x(t) может быть восстановлена по последовательности x(i) единственным образом, за исключением, быть может, изолированного множества точек.
Другими словами, теорема Котельникова утверждает, что непрерывная реализация x(t) может быть восстановлена по бесконечному временному ряду x(i) однозначно, если спектральный состав реализации ограничен и максимальная частота fmax в спектре реализации меньше или равна частоте Найквиста: fmax<Fn или fmax=Fn. Если это условие не выполняется, т.е. в спектре исходной непрерывной реализации содержатся частоты, бльшие частоты Найквиста (fmax>Fn), то при восстановлении реализации по ее дискретному представлению неизбежно возникнут неоднозначности, которые называются ошибками маскировки (подмены) частот.
Дискретизация сигнала во времени - это преобразование непрерывного аналогового сигнала в последовательность его значений в дискретные моменты времени. Эти значения называются отсчетами или выборками. В результате дискретизации непрерывного синусоидального сигнала (рис. 2.1,а) получается дискретный сигнал, показанный на рис. 2.1,6.
16. Дискретное преобразование Фурье. Свойства дискретного преобразования Фурье.
Формулы преобразований
Прямое преобразование:
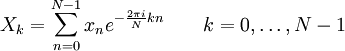
Обратное преобразование:
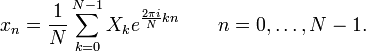
Обозначения:
N — количество значений сигнала, измеренных за период, а также количество компонентов разложения;
—
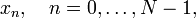измеренные
значения сигнала (в дискретных временных
точках с номерами
,
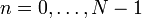которые являются входными данными для
прямого преобразования и выходными
для обратного;
—
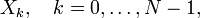Nкомплексных
амплитуд синусоидальных сигналов,
слагающих исходный сигнал; являются
выходными данными для прямого
преобразования и входными для обратного;
поскольку амплитуды комплексные, то
они обозначают одновременно и амплитуду
и фазу;
—
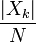обычная
(вещественная) амплитуда k-го синусоидального
сигнала;
arg(Xk) — фаза k-го синусоидального сигнала (аргумент комплексного числа);
k — частота k-го сигнала, равная
,
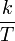где T
— период времени, в течение которого
брались входные данные.
Свойства
линейность
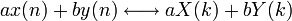
сдвиг по времени
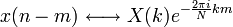
периодичность
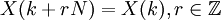
выполняется Теорема Парсеваля
обладает спектральной плотностью S(k) = | x(k) | 2
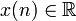
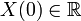
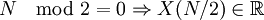Стоит
отметить, что нулевая гармоника является
суммой значений сигнала.
17. Узкополосные сигналы. Комплексное представление узкополосных сигналов.
Сигнал называется узкополосным , если его спектральная плотностьотлична от 0. Лишь в lim-ах частотных интервалов шириной П, образующих окрестности точек +/- W0, g1 выполниться условие: П / W0<<1.
Комплексное представление УС.
В теореме линейныхэлек. Цепей шир. Рспространен метод комплексных амплитуд, согласно кот. Гармонические колебания представляются кА реаль. Или мнимая часть комплексной формул.:
Um*cos(w0t+фи0) = Re[Um *ejфи0*ejw0t]
Um*sin(w0t+фи0) = Im[Um *ejфи0*ejw0t]
Um *ejфи0 – комплекс.амплитуда.
Um *ej(w0t+фи0)-мгновенный комплекс.
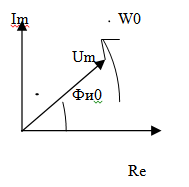
С физ.точки зрения УС представляют собой квазигармонические колебания.
Обобщим метод комплексных амплитуд, УС след вида:
S(t)=As(t)*cos(w0t)-Bs(t)*sin(w0t)
Введем комплексную низкочастотную функцию назваемуюкомплексной огибающей УС S(t)
Us(t)=As(t)+jBs(t).
Легко показать, что сигнал S(t) равен: S(t)=Re[Us(t)*eiw0t]
Таким образом комплексная огибающая УС играет ту же роль, что и комплексная амплитуда по отношению к простому гармоническому колебанию.Однако комплексная огибающая в общем случае зависит от времени.
Вектор Us(t) совершает некоторое движение в компл.плоскости, изменяясь как по амплитуде , так и по направлению.