8. Ортогональные сигналы и обобщённые ряды Фурье. Энергия сигнала, представленного в форме обобщённого ряда Фурье. Ортогональные сигналы и обобщённые ряды Фурье
Два сигнала Uи
V, называются ортогональными,
если их скалярное произведение равно
нулю. (U,V)=0
. Пусть Н гильбертово пространство
сигналов с конечным значение энергии.
Сигналы данного пр-ва определены на
конечном отрезке [t1,t2]
или бесконечно отрезках времени.
Предположим что на этом отрезке задана
беск. система ф-й {Uo,U1,…,Um,…}.
При чем для каждых
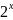функции выполняется условие:
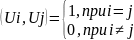в
этом случае говорят, что в пр-ве задано
ортонормированный базис.
Разложим произвольный
сигнал S(t)
из пространства Н в ряд следующего вида:
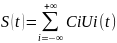
Данное представление называется обобщенным рядом Фурье для сигнала S(t), при этом коэффициенты ряда Сi находятся следующим аналогичным образом:
Умножим обе части
равенства на произвольный элемент,
ортонормированного базиса, а потом
проинтегрируем:
;
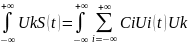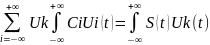
В силу ортонормированности
базиса в левой части равенства отличное
от нуля базиса те слогаемые для которых
I=k: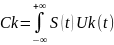
Возможность представления сигналов посредством обобщенных рядов Фурье, играет важное практическое значение. Вместо того чтобы изучать функциональную зависимость в несчетном множестве точек, мы получаем возможность характеризовать сигналы счетной системы коэффициентов обобщенного ряда Фурье.
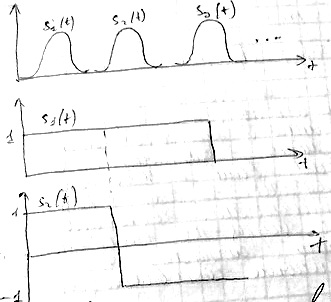
Энергия сигнала, представленная в виде обобщ. Ряда Фурье
Квадрат суммы носит название энергии сигнала именно такая энергия выделяется в резисторе, с сопротивлением 1 Ом, если к нему приложено напряжение S(t):Es = ||S||²
Рассмотрим некоторый сигнал S(t) разложенный в обобщенный ряд Фурье, найдем энергию этого сигнала
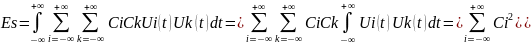
Энергия сигнала есть сумма энергии всех компонент, из которых складывается обобщенный ряд Фурье.
9. Оптимальность разложения сигнала по ортогональному базису. Конечномерный случай
Ортогональный
базис — базис,
составленный из попарно ортогональных
векторов. Ортонормированный базис
удовлетворяет еще и условию единичности
нормы всех его элементов. То есть это
ортогональный базис с нормированными
элементами. Последнее удобно записывается
при помощи символа Кронекера:
то есть скалярное произведение каждой
пары базисных векторов равно нулю, когда
они не совпадают i
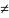j
и равно единице при совпадающем индексе,
то есть когда берется скалярное
произведение любого базисного вектора
с самим собой. Очень многое записывается
в ортогональном базисе гораздо проще,
чем в произвольном, поэтому очень часто
стараются использовать именно такие
базисы, если только это возможно или
использование какого-то специального
неортогонального базиса не дает особых
специальных удобств. Или если не
отказываются от него в пользу базиса
общего вида из соображений общности.
Ортонормированный базис является
самодуальным (дуальный ему базис
совпадает с ним самим). Поэтому в нём
можно не делать различия между верхними
и нижними индексами, и пользоваться,
скажем, только нижними (как обычно и
принято, если конечно при этом используются
только ортонормированные базисы).
Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически.
Коэффициенты
в разложении вектора по ортогональному
базису:
