6. Геометрические методы в теории сигналов. Пространства сигналов. Понятие координатного базиса. Пространства сигналов

1)Линейное; 2) Нормированное линейное; 3) Метрическое

Линейное пространство сигналов

ПустьМ={S1(t),S2(t),…,Sn(t)} – множ-во сигналов М образуют вещественное линейное пространство, если справедлива след.аксиома:

1)Любой сигнал принадлежит данному мн-ву, при любых зн-яхt принимает только веществ.зн-я.

U(t)€MU(t), V(t)= M

2) Для любых двух сигналов для данногомн-ва существует их сумма W(t)=U(t)+V(t), где W(t)€M

3)Для любого сигнала Sи любого вещественного числа α существует сигнал f(t), S(t) )€M, α

f(t)=αS(t)€M

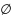4)Мн-во М содержит нулевой элемент такой, что U(t) €M, U(t)+ =U(t)

Если математич. модели сигналов принимают комплексное зн-е, то допуская в А.З. умн-е на комплексное число М ввести понятие комплексного линейного пр-ва.

Нормированное линейное пространство сигналов

Для того чтобы продолжить геометрич. трактовку сигнала необходимо ввести новое понятие которое по своему смыслу соответствует длине вектора(матем.длину вектора называют нормой)

Линейное пр-во сигналов Lявл-ся нормированным, если каждому вектору из этого пр-ва однозначно S(t)€Lсопоставлено число ||S|| называемой нормой сигнала/вектора. При этом выполняется след.аксиома:

||S||>0; ||S||=0 только в этом случае S=0.

Для любого α, S€L, ||αS||=α||S||

Если Sи р€M, то вып-ся неравенство треуг-ка ||S||+||р||≥||S+р||

Нормированное линейное пространство с конечной величиной нормы называется пространством функции с интегрируемом квадратом.

Метрическое пространство сигналов

Линейное пр-во L становится метрическим, если каждой паре эл-тов из этого пр-ва сопоставлено некоторое неотрицательное число ρ=(U,V), называемое метрикой или расстоянием между этими эл-тами. Метрика независима от м-ба ее определения подчиняться правилам:

ρ(U,V)=ρ(V,U)

ρ(U,V)= 0

Для любых Р,U,V выполняется ρ(U,Р)+ρ(Р,V) ρ(U,V)

Обычно метрику определяют как норму разности двух сигналов. ρ(U,V)=||U-V||; ρ(U)=||U- ||

Если знаем метрику то можно узнать что один сигнал аппроксимирует другой.

Понятие координатного базиса.

Как и в любом трехмерном пр-ве, в линейном пр-ве сигналов можно выделить спец. подмнож-ваиграющие роль координатных осей. Говорят, в вещественном мн-ве пр-ве сигналов совокупность векторов (сигналов) из мн-ва М явл-ся линейно независимыми если равенство выполняется (только когда 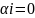). Система линейно независимых векторов образует координатный базис в линейном простр-ве. Если дано разложение некоторого сигнала S(t) в виде: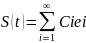 , то числа С1, С2,…,Сiявляются проекциями данного сигнала относительно выбранного базиса. Задача в теории сигналов-числобазиснх векторов, как правило, неограниченно велико. Таки пр-ва называются бесконечномерными.

7. Теория ортогональных сигналов. Ортогональные и квазиортогональные сигналы.

Два сигнала называются ортогональными, если имеют нулевое скалярное произведениеu(t), v(t)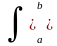 = u(t)v(t) dt = 0.Соответственно, два таких сигнала в своем функциональном пространстве являются взаимно перпендикулярными , полностью независимыми друг от друга (некоррелированными, r = cos, и имеют нулевую энергию взаимодействия (E_uv = 0).

На рисунке 2.3.1 приведены примеры взаимно ортогональных сигналов. Нулевое скалярное произведение двух левых сигналов обеспечивается их формой (равна нулю сумма положительных и отрицательных значений произведения сигналов), а двух правых - взаимным расположением (ненулевые значения сигналов не имеют общих координат).

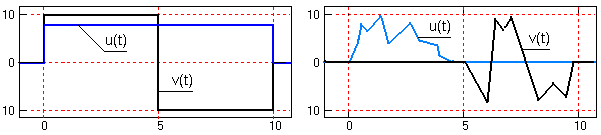
Энергия и мощность суммы ортогональных сигналов обладают свойством аддитивности, т.к. имеют нулевое значение скалярного произведения и, соответственно, нулевую энергию взаимодействия.

Свойство ортогональности: x(t) (t) dt = 0.Если все косинусные составляющие сигнала x(t) превращаются в ортогональные им синусные составляющие сигнала , а синусные – в ортогональные им косинусные, то и сигналы x(t) и должны быть ортогональны. Из теоремы Парсеваля следует: x(t) (t) dt = X^*(f) (f).Функция X^*(f) (f) = -X^*j sgn(f)X(f) = -j sgn(f)|X(f)|² является нечетной, а поэтому определенный интеграл от этой функции по симметричным относительно нуля пределам равен нулю.