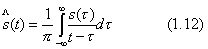- •1. Общие понятия передачи информации.
- •2. Обобщённая структурная схема системы передачи информации.
- •3. Каналы связи и их характеристики.
- •4. Классификация сигналов.
- •5. Динамическое представление сигналов.
- •6. Геометрические методы в теории сигналов. Пространства сигналов. Понятие координатного базиса. Пространства сигналов
- •7. Теория ортогональных сигналов. Ортогональные и квазиортогональные сигналы.
- •8. Ортогональные сигналы и обобщённые ряды Фурье. Энергия сигнала, представленного в форме обобщённого ряда Фурье. Ортогональные сигналы и обобщённые ряды Фурье
- •Энергия сигнала, представленная в виде обобщ. Ряда Фурье
- •9. Оптимальность разложения сигнала по ортогональному базису. Конечномерный случай
- •Бесконечномерный случай
- •10. Спектральный анализ периодических сигналов. Ряд Фурье. Спектральный анализ периодических сигналов.
- •Ряд Фурье.
- •11. Спектральный анализ непериодических сигналов. Преобразование Фурье.
- •12. Преобразование Фурье. Основные свойства преобразования Фурье.
- •13. Сигналы с ограниченным спектром. Идеальные низкочастотный и полосовой сигналы.
- •14. Ортогональные сигналы с ограниченным спектром.
- •15. Теорема Котельникова. Дискретизация сигналов.
- •16. Дискретное преобразование Фурье. Свойства дискретного преобразования Фурье.
- •17. Узкополосные сигналы. Комплексное представление узкополосных сигналов.
- •18. Узкополосные сигналы. Физическая огибающая, полная фаза, мгновенная частота. Свойства физической огибающей и мгновенной частоты узкополосного сигнала.
- •19. Аналитический сигнал. Преобразование Гильберта.
- •20. Элементы корреляционного анализа аналоговых сигналов.
- •21. Элементы корреляционного анализа дискретных сигналов.
- •22. Шумоподобные сигналы.
- •23. Аналоговые методы модуляции.
- •24. Аналоговые методы модуляции. Амплитудная модуляция.
- •25. Аналоговые методы модуляции. Угловая модуляция.
- •26. Цифровые методы модуляции.
- •27. Цифровые методы модуляции. Амплитудная модуляция.
- •28. Цифровые методы модуляции. Фазовая модуляция.
- •29. Цифровые методы модуляции. Частотная модуляция.
- •30. Дискретизация сигналов по времени.
- •31. Аналого-цифровое преобразование сигналов.
- •32. Нелинейное квантование. Компандирование.
- •33. Цифро-аналоговое преобразование сигналов.
- •34. Методы разностного квантования аналоговых сигналов. Дельта-модуляция.
- •35. Системы многоканальной передачи информации.
- •36. Системы передачи информации с частотным разделением каналов.
- •37. Системы передачи информации с временным разделением каналов.
- •38. Системы передачи информации с кодовым разделением каналов.
18. Узкополосные сигналы. Физическая огибающая, полная фаза, мгновенная частота. Свойства физической огибающей и мгновенной частоты узкополосного сигнала.
Комплексную огибающую можно представить показательной форме.
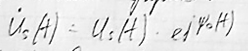
![]() -вещественная
функция, зависящая от времени и принимающая
только неотрицательные значения.
-вещественная
функция, зависящая от времени и принимающая
только неотрицательные значения.
Us(t) – физическая огибающая.
Ψ0(t)-медленно изменяющаяся во времени начальная фаза узкополосного сигнала.
Симфазная и квадратурная амплитуды связаны с физической огибающей и начальной фазой следующим соотношением:
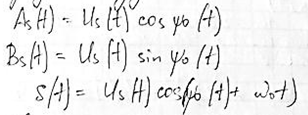
Введём полную фазу узкополосного колебания и определим мгновенную частоту сигнала.
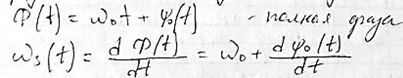
Узкополосный сигнал общего вида представляет собой сложное колебание, получающееся при одновременной модуляции несущего колебания как по амплитуде, так и по фазовому углу.
Свойства физической огибающей узкополосного сигнала.
Выразим физическую огибающую через синфазную и квадратурную амплитуды.
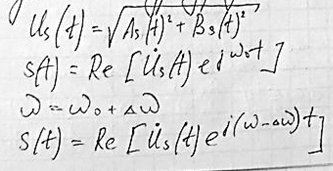
Физическая огибающая является модулем комплексной огибающей, остаётся неизменной.exp в степени=1)
Следующее свойство физической огибающей состоит в том, что в каждый момент времени значение сигнала | S(t)|≤Us(t). Знак равенства получается когда cos(ω0t)=1, но при этом производная сигнала и его огибающей будут равны.
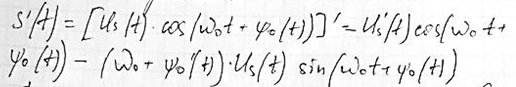
Важность понятия огибающей обусловлена тем, что в радиотехнике широко используются специальные устройства- амплитудные детекторы, которые могут достаточно точно воспроизводить физическую огибающую узкополосного сигнала.
Свойства мгновенной частоты узкополосной огибающей.
Если комплексная огибающая сигнала представляется вектором, который вращается на комплексной плоскости с неизменной угловой скоростью, то мгновенная частота узкополосного сигнала постоянна во времени. Данному сигналу соответствует квази гармоническое колебание промодулированное по амплитуде, но не по фазовому углу.
В общем случае мгновенная частота сигнала представляется по формуле:
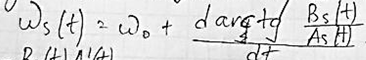
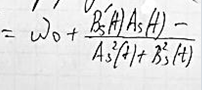
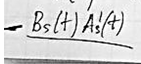
19. Аналитический сигнал. Преобразование Гильберта.
|

 При этом
При этом