Регрессионный анализ

- математико-статистический метод исследования зависимости одной случайной величины (критериальной переменной) от одной или нескольких независимых переменных (предикторов, регрессоров).

Замечание

Термин «зависимость» понимается здесь как «математическая зависимость», которой в определенном смысле наилучшим образом отвечают имеющиеся статистические данные, и не означает в общем случае наличие причинно-следственных связей между наблюдаемыми переменными.

В математической статистике понятия «корреляция» и «регрессия» неотделимы от понятия «стохастическая зависимость», вместе с тем они имеют четкое различие, отраженное в целях соответствующих исследований: собственно корреляционный анализ ориентирован на обнаружение корреляционной зависимости между рассматриваемыми признаками и оценку тесноты их связи, тогда как регрессионный анализ предполагает выявление и исследование формы зависимости критериальной переменной от предикторов.

Задачи регрессионного анализа

• Выбор предикторов, оказывающих значительное влияние на вариацию критериальной переменной, установление вида уравнения регрессии в соответствии с сущностью изучаемого явления.

• Оценка неизвестных параметров регрессионной модели, статистическая проверка их значимости.

• Оценка статистической надежности уравнения регрессии.

• Оценка адекватности и точности регрессионной модели, включающая проверку случайности остаточной компоненты критериальной переменной, проверку нормальности распределений критериальной переменной и остаточной компоненты, проверку равенства нулю математического ожидания остаточной компоненты, проверку равенства дисперсий и попарной некоррелированности остаточных компонент для проведенных наблюдений, оценку остаточной дисперсии.

• Изучение влияния отдельных предикторов на вариацию критериальной переменной.

66. Аддитивная модель регрессии. Основной подход к построению математических моделей регрессии. Множественная линейная модель регрессии.

Аддитивная модель регрессии

При описании исследуемой зависимости с помощью математической символики она обычно представляется как сумма двух составляющих: функциональной зависимости значения y критериальной переменной Y от возможных значений x₁, x₂,…, x_k предикторов X₁, X₂,…, X_k и возмущения ε – остаточной компоненты, отражающей случайность в изменении значений зависимой переменной Y под влиянием других факторов, отличных от X₁, X₂,…, X_k:

.

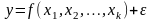Основной подход к построению математических моделей регрессии

В определенном классе многомерных функций подбирается такая функция , при которой остаточная компонента будет минимальной по некоторой статистической мере, т.е. находится аналитическое выражение, наиболее полно в рамках применяемой модели и выбранного критерия оптимальности отражающее математическую зависимость переменной Y от переменных X₁, X₂,…, X_k.

Множественная линейная модель регрессии

Общая формулировка

,

где - известные функции переменных x₁, x₂,…, x_k;

- параметры модели - константы, подлежащие определению.

67. Матричный вид системы уравнений, связывающих выборочные значения критериальной переменной и предикторов со значениями неизвестных параметров модели.

68. Предпосылки регрессионного анализа. Уравнение множественной линейной регрессии.

Предпосылки регрессионного анализа

1. Для каждого наблюдения распределение остаточной компоненты не зависит от значений предикторов.

2. Математическое ожидание остаточной компоненты во всяком наблюдении равно нулю:

.

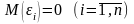Такое требование естественно полагать выполненным, поскольку функциональная компонента регрессионной модели должна учитывать систематическую тенденцию в изменении значений переменной Y.

3. Дисперсия остаточной компоненты одинакова для всех наблюдений:

.

4. Для любых двух наблюдений остаточные компоненты не коррелированны:

.

5. Для каждого наблюдения распределение вероятностей остаточной компоненты подчинено закону Гаусса.

Данное допущение часто основывается на центральной предельной теореме, состоящей в том, что если случайная величина обусловлена взаимодействием большого числа других случайных величин, причем ни одна из них не оказывает доминирующего влияния на общий результат, то распределение результирующей случайной величины близко к нормальному.

Из условий Гаусса - Маркова непосредственно следует, что:

• для i-го наблюдения критериальная переменная Y подчинена нормальному закону распределения вероятностей с математическим ожиданием , являющимся функцией только предикторов, и дисперсией , не зависящей от реализаций случайного вектора (X₁, X₂,…, X_k);

• для произвольных двух наблюдений остаточные компоненты стохастически не независимы.