Замечание

Доказано, что в классе всех возможных оценок, не совпадающих тождественно (т.е. для любого ) с неизвестным параметром θ, оценки, наилучшей в смысле среднеквадратического подхода, не существует.

Эффективность

Несмещенная точечная оценка параметра θ называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок данного параметра, вычисленных по выборкам одного и того же объема n.

Замечание

Сравнение произвольных несмещенных оценок θ*, θ** параметра θ "в среднеквадратичном" сводится к сопоставлению дисперсий данных оценок, так как в этом случае θ=Мθ*=Мθ**, следовательно, определяющее неравенство эквивалентно соотношению Dθ*≤Dθ**. Поэтому эффективная оценка является наилучшей при сравнении в смысле среднеквадратического подхода.

В классе несмещенных точечных оценок параметра θ существует его эффективная оценка. Если θ*, θ** — эффективные оценки этого параметра, то с вероятностью, равной единице, они совпадают: .

11. Метод моментов К.Пирсона определения точечных оценок неизвестных параметров распределения.

Метод моментов Пирсона

Для всякой случайной величины, закон распределения вероятностей которой полностью обусловливается некоторым параметром θ=(θ₁, θ₂,…, θ_q), любой (начальный или центральный) теоретический момент произвольного порядка, согласно соответствующей формулировке, функционально зависит от компонент θ₁, θ₂,…, θ_q этого параметра.

Точечная оценка неизвестного векторного параметра θ по методу К. Пирсона осуществляется с помощью q теоретических моментов различных порядков, выбираемых в зависимости от постановки задачи (начальных, либо центральных, возможно, тех и других одновременно).

В качестве точечной оценки параметра θ=(θ₁, θ₂,…, θ_q) принимается такой вектор , при котором каждый из используемых теоретических моментов совпадает с соответствующим выборочным моментом, вычисленным по имеющимся эмпирическим данным x₁, x₂,…, x_n.

Таким образом, для нахождения искомых приближенных компонент 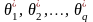строится система q уравнений вида

или

,

в которых x₁, x₂,…, x_n рассматриваются как фиксированные величины.

В случае принципиальной разрешимости данной, вообще говоря, нелинейной системы уравнений относительно переменных результатом аналитического (или же численного) решения станут определяемые по выборке q функций (либо q конкретных чисел):

,

,

,

составляющих точечную оценку (или же реализацию точечной оценки) неизвестного векторного параметра по методу моментов.

Достаточное условие состоятельности оценки, найденной по методу Пирсона

Если полученные с помощью метода моментов функции непрерывно зависят от переменных x₁, x₂,…, x_n, то точечная оценка параметра θ=(θ₁, θ₂,…, θ_q) состоятельная.

Пример

Пусть (x₁, x₂,…, x_n) - выборка объема n из генеральной совокупности с распределением, подчиненным нормальному закону с неизвестными параметрами µ, σ.

Принимая во внимание теоретико-вероятностный смысл параметров нормального распределения, точечные оценки µ*, σ* находятся по первому начальному и второму центральному моментам:

,

.

Очевидно, что данная система уравнений может быть представлена следующим образом:

,

или

.

12. Метод максимального правдоподобия Р.Фишера нахождения точечных оценок неизвестных параметров распределения.