Метод максимального правдоподобия Фишера

Функцией правдоподобия для выборки (x₁,x₂,…,x_n) в случае непрерывно распределенной генеральной совокупности (непрерывной случайной величины) ξ с зависящей от параметра θ=(θ₁, θ₂,…, θ_q) плотностью распределения вероятностей φ(x,θ₁,θ₂,…,θ_q) называется функция

.

Указанная функция представляет собой плотность распределения n-мерного случайного вектора (x₁, x₂,…, x_n), все компоненты которого независимы в совокупности и имеют такое же распределение, что и наблюдаемый признак ξ.

Функция правдоподобия в случае дискретно распределенной генеральной совокупности (дискретной случайной величины) ξ с зависящей от параметра θ=(θ₁, θ₂,…, θ_q) функцией вероятностей f(x,θ₁,θ₂,…,θ_q) определяется аналогично:

.

Значение функции правдоподобия для выборки (x₁,x₂,…,x_n) в данном случае определяется как соответствующая ей вероятность.

В качестве оценки неизвестного параметра θ=(θ₁, θ₂,…, θ_q) по методу Р.Фишера берется вектор , максимизирующий вероятность получить в n наблюдениях имеющуюся выборку (x₁,x₂,…,x_n), т.е. те значения , при которых функция правдоподобия достигает максимума при фиксированных значениях x₁, x₂,…, x_n.

Максимум функций и достигается в одной и той же точке, поэтому при выкладках удобно использовать логарифмическую функцию правдоподобия.

Если функция правдоподобия дифференцируема по переменным θ₁, θ₂,…, θ_q, то требуемую оценку находят из необходимых условий экстремума функции , решая систему q уравнений:

.

Пример

Оценим по выборочным данным x₁, x₂,…, x_n неизвестные параметры µ, σ² нормального распределения генеральной совокупности, используя метод Фишера.

Функция правдоподобия представима следующим образом:

.

Отвечающая ей логарифмическая функция имеет вид:

.

Из системы уравнений правдоподобия:

.

находим искомые оценки:

.

13. χ²-распределение (Пирсона), числовые характеристики распределения. Примеры полезных статистик, имеющих χ²-распределение.

14. Распределение Стьюдента, числовые характеристики распределения. Примеры полезных статистик, имеющих t-распределение.

15. Распределение Фишера-Снедекора. Свойство распределения. Примеры полезных статистик, имеющих F-распределение.

16. Основные таблицы математической статистики.

17. Понятие асимптотически нормальной точечной оценки параметра распределения. Примеры полезных статистик, обладающих свойством асимптотической нормальности.

18. Понятия: «доверительный интервал», «точный доверительный интервал», «асимптотический доверительный интервал», «асимптотический точный доверительный интервал».

19. Схема построения точного доверительного интервала.

20. Схема построения асимптотического точного доверительного интервала.

21. Доверительный интервал для математического ожидания (генеральной средней) нормального распределения при известной генеральной дисперсии.

Полагается, что (x₁, x₂,…, x_n) - независимая повторная выборка объема n из генеральной совокупности с распределением N(µ,σ²).

Ди для математического ожидания (генеральной средней) µ при известной дисперсии σ2

• Выбирается функция , имеющая распределение N(0,1).

Следовательно, , где - функция Лапласа, т.е. функция распределения случайной величины не зависит от параметра µ.

• Полагается, что .

Обозначим символами , квантили распределения N(0,1) уровней соответственно , :

; .

Из соотношения

вытекает, что

; .

Таким образом,

_.

Поскольку - нечетная функция, то

.

Итак,

_.

• Решая относительно µ полученное двойное неравенство:

_,

находим, что при известной дисперсии интервальная оценка математического ожидания заданной надежности γ представима в следующем виде:

или (при другом используемом в литературе обозначении квантили):

_.

Точность оценки .

Значение квантили может быть найдено:

• или из статистической таблицы 1 (Значения функции Лапласа , где случайная величина Т имеет стандартное нормальное распределение), исходя из соотношения:

,

• или с помощью встроенной статистической функции Microsoft Excel НОРМСТОБР(вероятность):

= НОРМСТОБР( ).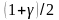

22. Доверительный интервал для математического ожидания (генеральной средней) нормального распределения при неизвестной генеральной дисперсии.

Полагается, что (x₁, x₂,…, x_n) - независимая повторная выборка объема n из генеральной совокупности с распределением N(µ,σ²).

• Используется функция , где - несмещенная оценка σ.

Выбранная статистика имеет не зависящее от параметра µ распределение Стьюдента с числом степеней свободы ν=n-1.

• Пусть 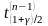, - квантили t-распределения уровней , , соответствующие надежности γ и числу степеней свободы, равному n-1.

В таком случае двойное неравенство

выполняется с вероятностью γ.

• Данное неравенство равносильно следующему неравенству:

.

Распределение Стьюдента симметрично, следовательно,

_.

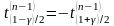Таким образом, при неизвестной дисперсии интервальная оценка надежности γ для математического ожидания имеет вид:

_;

эквивалентная форма:

_.

• Выбирается функция , где - смещенная выборочная дисперсия.

Данная функция имеет не зависящее от σ² распределение с числом степеней свободы, равным n-1.

• Полагая, что 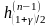, - квантили уровней , , отвечающие надежности γ и числу n-1 степеней свободы -распределения, интервальная оценка для дисперсии при неизвестном математическом ожидании приобретает вид:

или (краткая запись):

_.

Значения квантилей 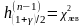, могут быть получены:

• или из статистической таблицы 3 на основании равенств:

; ;

• или с помощью встроенной статистической функции Microsoft Excel ХИ2ОБР(вероятность;степени_свободы), согласно соотношениям:

= ХИ2ОБР( ;n-1);

= ХИ2ОБР( ;n-1).

23. Доверительный интервал для дисперсии нормального распределения при известном математическом ожидании (генеральной средней).

• Применяется функция , где - несмещенная оценка параметра σ² при известном значении параметра µ.

Взятая функция имеет не зависящее от σ² распределение с числом степеней свободы, равным n.

• Если , - квантили уровней , , соответствующие надежности γ и числу n степеней свободы распределения Пирсона, тогда

_.

• Решая двойное неравенство относительно σ², находим, что интервальная оценка заданной надежности γ для дисперсии при известном математическом ожидании представима таким образом:

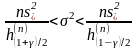
или (краткая запись):

.

Значения квантилей , могут быть получены:

• или из статистической таблицы 3 (Значения вероятностей , где случайная величина имеет распределение Пирсона с числом степеней свободы, равным ν), исходя из равенств:

; ;

• или с помощью встроенной статистической функции Microsoft Excel ХИ2ОБР(вероятность;степени_свободы), определяющей значение по известному значению вероятности и заданному числу степеней свободы ν соответствующего распределения Пирсона:

= ХИ2ОБР( ;n);

= ХИ2ОБР( ;n).

24. Доверительный интервал для дисперсии нормального распределения при неизвестном математическом ожидании (генеральной средней).

• Выбирается функция , где - смещенная выборочная дисперсия.

Данная функция имеет не зависящее от σ² распределение с числом степеней свободы, равным n-1.

• Полагая, что , - квантили уровней , , отвечающие надежности γ и числу n-1 степеней свободы -распределения, интервальная оценка для дисперсии при неизвестном математическом ожидании приобретает вид:

или (краткая запись):

_.

Значения квантилей , могут быть получены:

• или из статистической таблицы 3 на основании равенств:

; ;

• или с помощью встроенной статистической функции Microsoft Excel ХИ2ОБР(вероятность;степени_свободы), согласно соотношениям:

= ХИ2ОБР( ;n-1);

= ХИ2ОБР( ;n-1).

Схема нахождения асимптотически точных доверительных интервалов

• Отыскивается случайная величина - функция выборочных данных x₁, x₂,…, x_n и параметра θ, такая, что при последовательность функций распределения (n=1, 2,…) сходится к независящей от параметра θ функции некоторого известного распределения.

Предполагается также непрерывность и обратимость относительно θ при любых фиксированных значениях x₁, x₂,…, x_n.

• Исходя из соотношения: , где γ - требуемая надежность доверительного интервала (известная величина), выбираются два положительных числа .

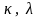Вычисляются квантили предельного распределения уровней и , т.е. числа , , для которых выполняются следующие равенства:

; .

• Решается относительно θ двойное неравенство:

.

25. Доверительное оценивание вероятности (генеральной доли признака) - параметра биномиального распределения - при большом и при малом числе наблюдений.

Определяется доверительный интервал для неизвестной, одинаковой для всех проводимых повторных наблюдений, вероятности р наступления некоторого случайного события А (генеральной доли объектов генеральной совокупности, обладающих признаком A).

а) при достаточно большом числе наблюдений

• В силу асимптотической нормальности относительной частоты (выборочной доли) события А, при значительном числе наблюдений (на практике, как правило, при n>30) распределение статистики почти совпадает с распределением N(0,1).

Следовательно, в таком случае функция распределения случайной величины практически не зависит от параметра р.

Значения x₁, x₂,…, x, указанные в записи , здесь понимаются как индикаторы события А:

,

при этом, очевидно, .

Если - квантиль уровня стандартного нормального распределения, то

.

Двойное неравенство

преобразованиями сводится к квадратному неравенству:

Отсюда

.

Таким образом, границы асимптотически точного доверительного интервала вычисляются согласно формулам:

или (в упрощенном виде)

.

Значение квантили уровня для стандартного нормального распределения вероятностей находится с помощью способов, изложенных выше.

в) при малом числе наблюдений

При малых значениях n отклонение распределения рассмотренной статистики от стандартного нормального распределения может оказаться весьма значительным, и замена, подобная предыдущей, становится недопустимой из-за возникающей большой погрешности.

В этом случае используется известная формула Бернулли:

.

Границы доверительного интервала при числе элементов выборки, обладающих признаком A, равном m, определяются из уравнений:

;

,

где γ - надежность интервальной оценки.

Корни указанных уравнений могут быть найдены с помощью какого-либо численного метода решения нелинейных уравнений (например, посредством метода последовательных приближений) или же могут быть получены из специальных таблиц по заданным значениям n, m, γ.

26. Понятие «статистическая гипотеза». Статистический критерий. Статистика критерия. Область отвержения гипотезы.

• Под статистической гипотезой понимается всякое предположение о распределении наблюдаемого признака (признаков).

Любая гипотеза, в том числе и статистическая, есть определенное утверждение, которое по отношению к реальной ситуации является или истинным, или ложным высказыванием, и не может характеризоваться в этом качестве никак иначе.

В статистической гипотезе речь может идти, в частности, о виде неизвестного распределения вероятностей, значениях его параметров или числовых характеристик, одинаковости (или различии) законов распределения наблюдаемых признаков, соответствии (или несовпадении) их теоретико-вероятностных характеристик, стохастической независимости (или зависимости) исследуемых признаков и тому подобном.

• Простой статистической гипотезой называется предположение о соответствии неизвестного распределения вероятностей отдельному конкретному распределению.