1. Понятия: «генеральная совокупность», «выборочная совокупность». Сущность выборочного метода.

Генеральная совокупность

Множество результатов всех обусловленных определенным комплексом условий мыслимых наблюдений над значениями одного или нескольких признаков называется генеральной совокупностью.

Замечание

Под генеральной совокупностью понимается множество всех потенциальных (в рамках данного комплекса условий наблюдения) объектов, как подлинно существующих, так и гипотетических.

Генеральная совокупность может содержать как конечное, так и бесконечное число объектов.

Пример

Если множество подлежащих изучению объектов есть группа проверяемых по определенным экономическим показателям однородных предприятий, реально функционирующих при заданных условиях, то, как правило, она не исчерпывает соответствующей генеральной совокупности и может быть мысленно дополнена схожими объектами.

Выборочная совокупность

В подавляющем большинстве прикладных задач, связанных с изучением случайных явлений, обследовать генеральную совокупность в целом (сплошным образом) практически не представляется возможным не только в случае бесконечного множества объектов, входящих в генеральную совокупность. Если число объектов ограничено, то, обычно, оно достаточно велико, что влечет чрезмерные временные, финансовые и иные затраты на проведение исследования.

Часть (подмножество) генеральной совокупности, содержащая конечное число объектов, отобранных для изучения, называется выборочной совокупностью.

Сущность выборочного метода состоит в вынесении научно обоснованного суждения об объективных свойствах генеральной совокупности по данным выборочной совокупности.

2. Вариационный ряд. Распределение выборки. Полигон распределения выборки Числовые характеристики распределения выборки: математическое ожидание, дисперсия, начальные и центральные моменты, эксцесс, коэффициенты асимметрии и вариации.

Вариационный ряд

Выборка представляет собой, обычно, неупорядоченное множество чисел. Анализ подобного несистематизированного статистического материала при большом количестве проведенных наблюдений часто весьма затруднителен, поэтому совокупность полученных эмпирических данных подвергается предварительной обработке и представляется в компактной и обозримой форме, позволяющей также во многих случаях снизить объемы расчетов.

• Элементы выборки ранжируют, т.е. располагают в порядке неубывания:

,

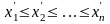где .

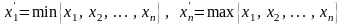• Ранжированный ряд выборочных значений 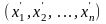группируют, т.е. имеющиеся статистические числовые данные объединяют в группы, каждая из которых содержит все одинаковые и только такие значения наблюдаемого признака.

Выборочное значение, соответствующее отдельной группе сгруппированного ряда статистических данных, называется выборочным вариантом.

Выборочные варианты принято обозначать строчной буквой с индексом, указывающим номер варианта в упорядоченной по возрастанию вариантов последовательности: 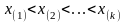, где k – общее число выборочных вариантов.

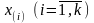Численность m_i отдельной группы сгруппированного ряда статистических данных называется частотой соответствующего выборочного варианта , здесь i – индекс варианта.

Отношение частоты m_i варианта x_(i) к объему n выборки (общей сумме частот) называется относительной частотой (или частностью) данного варианта и обозначается символом ω_i:

.

Возрастающая последовательность вариантов с отвечающими им частотами , представленная в виде таблицы:

,

называется вариационным рядом.

Пример

Выборка: X⁽¹⁰⁾=(2, 1, 2, 4, 3, 2, 1, 1, 2, 4).

Ранжированный ряд: (1, 1, 1, 2, 2, 2, 2, 3, 4, 4).

Группированный ряд: .

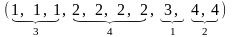Вариационный ряд: .

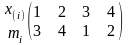Распределение выборки

Пусть 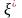- дискретная случайная величина, множество возможных значений которой совпадает с совокупностью всех вариантов выборки (x₁, x₂,…, x_n).

Поставим в соответствие каждому из значений вероятность, равную его относительной частоте .

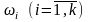Распределение вероятностей, определенное рядом

,

называется распределением выборки (x₁, x₂,…, x_n) (эмпирическим распределением наблюдаемого признака ξ).

Пример

Ряд распределения для выборки X⁽¹⁰⁾=(2, 1, 2, 4, 3, 2, 1, 1, 2, 4):

.

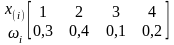Полигон распределения выборки

Конечнозвенная ломаная кривая, последовательно соединяющая отрезками прямых линий точки плоскости с координатами 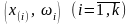, называется полигоном распределения выборки.

Пример

Полигон распределения для выборки (2, 1, 2, 4, 3, 2, 1, 1, 2, 4):

Числовые характеристики распределения выборки – точечные оценки числовых характеристик наблюдаемого признака

В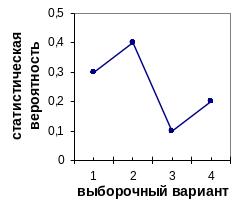 ыборочное среднее

.

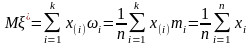Обозначается символом .

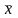Выборочная дисперсия

.

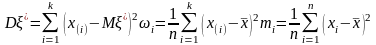Обозначается символом .

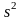Выборочное среднее квадратическое отклонение

.

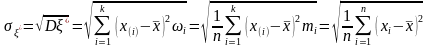Обозначается символом .

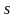Выборочный начальный момент j-го порядка

.

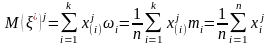Обозначается символом .

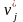Замечание

Выборочный начальный момент первого порядка совпадает с выборочным средним: .

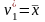Выборочный центральный момент j-го порядка

.

Обозначается символом .

Замечание

Выборочный центральный момент второго порядка есть выборочная дисперсия: .

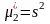Соотношения между центральными и начальными выборочными моментами

;

;

.

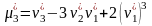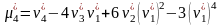Выборочный коэффициент асимметрии

.

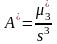Выборочный эксцесс

.

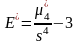Выборочный коэффициент вариации

.

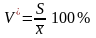Пример

Математическое ожидание и дисперсия распределения выборки (2, 1, 2, 4, 3, 2, 1, 1, 2, 4):

.

.

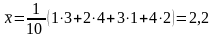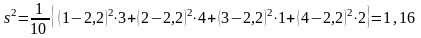3. Состоятельность, несмещенность и асимптотическая нормальность выборочного среднего. Состоятельность, смещенность и асимптотическая нормальность выборочной дисперсии. Несмещенные оценки дисперсии.

• Выборочное среднее , рассматриваемое в качестве случайной величины, обладает следующими свойствами.

Состоятельность. Последовательность случайных величин 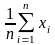(n=1, 2,…) сходится по вероятности к математическому ожиданию наблюдаемого признака:

.

Несмещенность. Каков бы ни был объем n выборки,

;

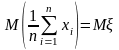Асимптотическая нормальность:

.

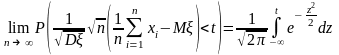Доказательство свойств

Состоятельность.

Элементы выборки (x₁, x₂,…, x_n) отбираются наудачу, независимо друг от друга, одинаковым способом, из одной и той же генеральной совокупности, поэтому все они, будучи случайными величинами, имеют одинаковое распределение вероятностей своих значений. Отсюда следует, что их математические ожидания 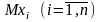совпадают с математическим ожиданием признака ξ: .

Таким образом, для последовательности результатов наблюдений x₁, x₂,…, x_n,… выполняются условия Закона больших чисел в форме Хинчина, в соответствии с которым

.

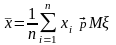Несмещенность выборочного среднего непосредственно вытекает из свойства линейности математического ожидания:

.

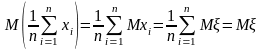Замечание

Несмещенность выборочного среднего означает отсутствие ошибки при систематическом использовании данной оценки. Вероятностное среднее всех возможных случайных значений при фиксированном объеме n выборки равно вероятностному среднему значению наблюдаемого признака.

Асимптотическая нормальность.

Элементы выборки (x₁, x₂,…, x_n) независимы и одинаково распределены. Тем самым выполнены условия применимости к последовательности x₁, x₂,…, x_n,… следствия из Центральной предельной теоремы Ляпунова, представимого в этом случае в виде:

.

Для завершения доказательства асимптотической нормальности выборочного среднего достаточно принять во внимание равенство:

.

• Выборочный начальный момент j-го порядка является состоятельной, несмещенной и асимптотически нормальной оценкой начального момента j-го порядка :

; ; .

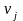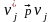• Выборочная дисперсия s² есть состоятельная, смещенная, асимптотически нормальная оценка дисперсии Dξ:

; ; .

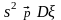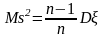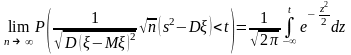Доказательство смещенности выборочной дисперсии s²

По известной из теории вероятностей формуле дисперсия выборочного среднего представима следующим образом:

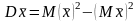
или, учитывая свойство несмещенности выборочного среднего, в виде

.

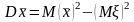(1)

Применяя к выражению , определяющему , свойство аддитивности дисперсии для сумм независимых случайных величин, находим другое представление дисперсии выборочного среднего:

.

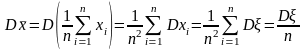(2)

Из уравнений (1), (2) следует, что

.

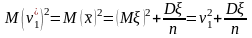(3)

Используя равенство 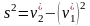, выражение (3) и свойство несмещенности , получаем

.
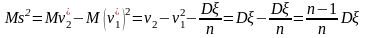