Теорема Гливенко - Кантелли

Если - эмпирическая функция распределения, построенная по независимой повторной выборке объема n из генеральной совокупности с неизвестной функцией распределения F_ξ(x), то для произвольного числа >0

.

Замечание

Теорема Гливенко – Кантелли, в сравнении с теоремой Бореля, устанавливает значительно более сильный результат, показывающий, что при неограниченном возрастании объема выборки n сходимость по вероятности эмпирической функции распределения к истинной функции распределения F_ξ(x) является не только поточечной, но и равномерной на числовой оси , т.е.

.

Данная теорема обосновывает возможность аппроксимировать функцию распределения наблюдаемого признака его эмпирической функцией распределения, тем более точной (почти достоверно), чем больше объем выборки.

В связи с этим обстоятельством, практически важным является вопрос о том, насколько быстро при последовательность эмпирических функций распределения приближается к неизвестной функции распределения F_ξ(x).

6. Теорема Колмогорова. Скорость сходимости последовательности эмпирических функций распределения при неограниченном возрастании объема выборки.

Теорема Колмогорова

Если - эмпирическая функция распределения, построенная по независимой повторной выборке объема n из неизвестного распределения с непрерывной функцией F_ξ(x), то при последовательность функций распределения

случайных величин

сходится к непрерывной функции

С ледствие

В условиях теоремы Гливенко - Кантелли скорость сходимости к нулю при имеет порядок, равный .

7. Свойства несмещенности и асимптотической нормальности эмпирической функции распределения.

Несмещенность

Эмпирическая функция распределения при любом значении переменной x имеет математическое ожидание, равное значению неизвестной функции распределения F_ξ(x) в данной точке:

.

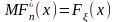Так как при определенном значении аргумента x для всех индикаторов их математическое ожидание совпадает со значением в этой точке теоретической функции распределения, т.е. , то

.

Следствие

Эмпирическая функция распределения при каждом значении своего аргумента характеризуется конечной дисперсией, монотонно убывающей с возрастанием объема выборки n пропорционально в соответствии с формулой:

Применяя свойство аддитивности дисперсии для суммы независимых случайных величин, учитывая далее, что для каждого выборочного значения , на основании соотношения:

находим

Асимптотическая нормальность

Неограниченное возрастание объема выборки n при произвольном фиксированном значении переменной x влечет равномерную сходимость последовательности функций распределения случайных величин

к интегральной функции стандартного нормального распределения:

.

Совокупность индикаторов удовлетворяет условиям Центральной предельной теоремы Ляпунова, в силу того, что индикаторы независимы между собой, имеют одинаковые конечные математические ожидания , дисперсии и абсолютные центральные моменты третьего порядка

Таким образом, согласно следствию из теоремы Ляпунова, функции распределения центрированных и нормированных сумм индикаторов , т.е. функции распределения величин:

при равномерно на числовой оси 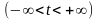сходятся к функции распределения стандартного нормального закона:

.

Для завершения доказательства свойства остается только принять во внимания следующие равенства:

.

8. Гистограмма, построение гистограммы. Достаточное условие сходимости последовательности гистограмм к теоретической плотности распределения при неограниченном возрастании объема выборки.