Несмещенные оценки дисперсии

• при известном математическом ожидании Мξ:

,

• при неизвестном математическом ожидании Мξ:

; .

Доказательство несмещенности оценок , ,

Так как элементы выборки одинаково распределены и независимы, то

;

.

Несмещенность вытекает из определяющего выражения для этой оценки дисперсии и следующих равенств:

.

4. Эмпирическая функция распределения, её основные свойства.

Эмпирическая функция распределения

Определение по выборке

Эмпирической функцией распределения, построенной по выборке (x₁,x₂,…,x_n), называется функция , определяемая при каждом значении действительного переменного x как отношение числа ν(x) элементов выборки, меньших x, к объему выборки n:

.

Определение по вариационному ряду

Эмпирическая функция распределения может быть найдена по вариационному ряду , используя следующее аналитическое представление:

Свойства эмпирической функции распределения

Из определения эмпирической функции распределения по вариационному ряду и из соотношения

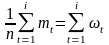
следует, что есть не что иное, как функция распределения выборки , и поэтому она обладает всеми свойствами, присущими интегральной функции распределения дискретной случайной величины, а именно:

• определена на всей числовой оси;

• принимает значения из отрезка [0;1];

• кусочно-постоянная;

• не убывает при возрастании аргумента x;

• непрерывна слева;

• имеет скачок значения в каждой точке , равный соответственно .

Пример

График эмпирической функции распределения выборки

(2, 1, 2, 4, 3, 2, 1, 1, 2, 4):

Замечание

Значение при любом значении переменной x зависит от выборки (x₁, x₂,…, x_n). Следовательно, данная функция при каждом значении своего аргумента есть случайная величина. Эмпирическая функция распределения , рассматриваемая в качестве случайной оценки теоретической функции распределения F_ξ(x), имеет следующие важные свойства.

5. Свойство состоятельности эмпирической функции распределения: теорема Бореля, теорема Гливенко - Кантелли.

Состоятельность

Последовательность эмпирических функций распределения при неограниченном возрастании объема выборки n сходится по вероятности к функции распределения F_ξ(x) наблюдаемого признака ξ.

Теорема Бореля

Для любого значения переменной x и произвольного числа >0

.

Из определения эмпирической функции распределения по выборке (x₁, x₂,…, x_n) непосредственно вытекает, что

,

где - индикатор (число успехов в одном наблюдении) случайного события :

.

Случайные величины независимы, одинаково распределены и, следовательно, имеют одно и то же конечное математическое ожидание:

.

Таким образом, для последовательности индикаторов 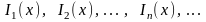выполняются условия применимости Закона больших чисел в форме Хинчина, согласно которому среднее арифметическое рассматриваемых случайных величин сходится по вероятности к их математическому ожиданию:

.

Замечание

Смысл предельного соотношения Бореля состоит в том, что для каждого конкретного значения переменной x при достаточно больших значениях объема выборки n практически достоверно, что значение эмпирической функция распределения отличается от значения неизвестной функции распределения F_ξ(x) признака ξ на величину, меньшую наперед заданного числа, сколь угодно малого.