7. Граничные условия для векторов электрического поля.

На поверхности раздела S двух изотропных сред, характеризуемых параметрами ₁ и ₂ соответственно, выделим достаточно малый элемент S, чтобы, во-первых, его можно было считать плоским, а во-вторых, чтобы в обеих средах распределение нормальной компоненты вектора можно было считать равномерным в пределах S.П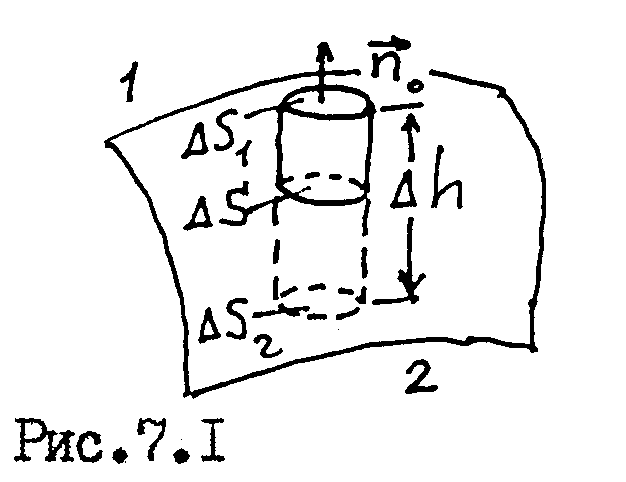 остроим на элементе S прямой цилиндр высотой h так, чтобы его основания находились в разных средах (рис.7.1), и применим к нему третье уравнение максвелла в интегральной форме:

, 7.1

где Sц – поверхность цилиндра, а V - его объем.

Так как поверхность Sц можно представить в виде суммы: , где – площади верхнего и нижнего оснований цилиндра соответственно, его боковая поверхность, то уравнение 7.1 принимает вид:

7.2

Устремим высоту цилиндра h к нулю так, чтобы его основания остава­лись в разных средах. При этом в пределе S₁ и S₂ совпадут с S. Так как элемент поверхности в уравнениях 7.1 и 7.2 совпадает по направлению с внешней нормалью к поверхности S_ц, то в результате предельного перехода получим следующие равенства:

, 7.3

где n₀ –орт нормали к площадке S, проведенной из второй среды в первую; D₁ и D₂ – значения вектора на границе раздела в первой и во второй средах соответственно, а D_1n и D_2n – проекции векторов на нормаль n₀. Переходя в уравнении 7.2 к пределу Ak->o, получаем с учетом 7.3:

7.4. Если заряд не сосредоточен на поверхности раздела, т.е. не является поверхностным, то при любой конечной величине объемной плотности заряда  правая часть 7.4 равна нулю, а нормальная компонента вектора непрерывна при переходе из одной среды в другую: 7.5. Особый интерес представляет случай, когда заряды распределены вдоль поверхности раздела в виде бесконечно тонкого слоя. Такие за­ряды называют поверхностными и характеризуют поверхностной плотностью _n, определяемой соотношением: ,7.6

где – элемент поверхности, – заряд этого элемента.Пусть теперь на границе раздела имеются поверхностные заряды с плотностью _n. В этом случае правая часть уравнения 7.1 уже не будет равна нулю. Считая распределение заряда на площадке равномерным (в противном случае нельзя считать равномерным распределение ), разделим обе части уравнения 7.4 на . В результате имеем:

. 7.7

Соотношение 7.7 показывает, что при переходе из одной среды в дру­гую нормальная компонента вектора претерпевает скачок, равный по­верхностной плотности заряда, распределенного вдоль границы раздела. Выражая в этом соотношении через с помощью равен­ства , получаем граничное условие для нормальных компонент вектора Е:

.7.8. Если на границе раздела отсутствуют поверхностные заряды, то ус­ловие 7.8 можно представить в виде:

7.9

7.9 показывает, что нормальная компонента вектора Е при переходе через незаряженную поверхность раздела двух сред пре­терпевает разрыв, величина которого определяется отношением диэлек­трических проницаемостей этих сред.

7.3. Условия для касательных составляющих векторов и

И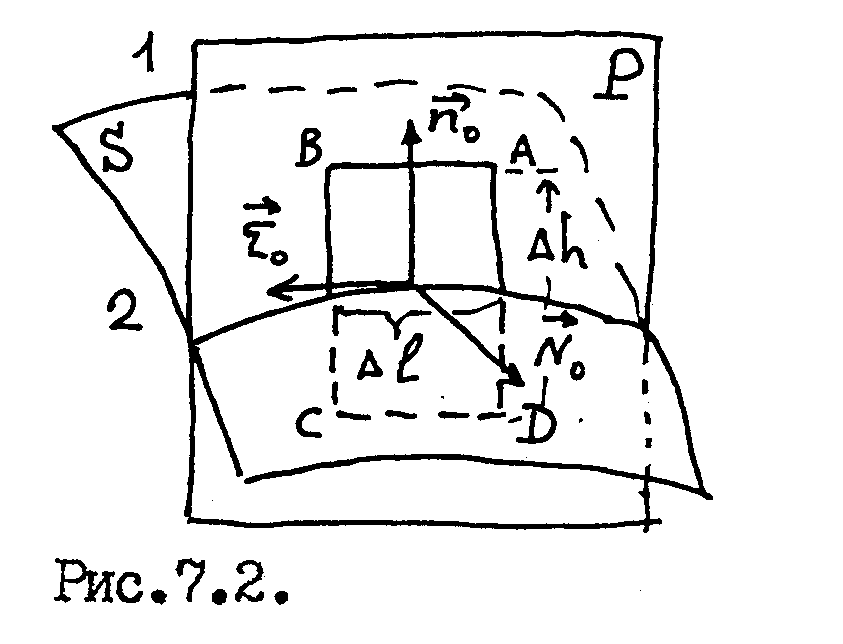 з произвольной точки на поверхности раздела S двух изотропных сред проведем из второй среды в первую единичную нормаль (рис. 7.2). Через проведем плоскость Р. На линии пересечения поверхности раздела и плоскости Р выделим достаточно малый отрезок так, чтобы выбранная точка находилась внутри этого отрезка. Размеры отрезка должны быть такими, чтобы, во-первых, его можно было считать прямолинейным, а во-вторых, чтобы в обеих средах касательную компоненту вектора можно было считать постоянной в пределах . В плоскости Р на отрезке построим прямоугольный контур АВСД высоты так, чтобы он находился в обеих средах. Проведём, кроме того, единичную касательную к отрезку и единичную нормаль к плоскости Р, образующую с обходом контура ABCD правовинтовую систему. Векторы , и также образуют правовинтовую систему и удовлетворяют соотношению:

.7.10 К контуру ABCD применим второе уравнение Максвелла в интегральной форме:

, 7.11.где S – площадь, охватываемая контуром ABCD, a .

Левую часть уравнения 7.11 можно представить в виде суммы четырех интегралов:

7.12

Устремим высоту контура ABCD к нулю так, чтобы стороны AB и CD оста­вались в разных средах и в пределе совпадали с . Учитывая, что на сторонах AB и CD дифференциал определяется равенствами и соответственно, и используя условие малости , получаем:

, 7.13

где и – значения вектора на границе раздела в первой и во второй средах соответственно, а и – проекции векторов и на направление .

Так как векторы и имеют конечные значения, то выполня­ются соотношения: . 7.14

Переходя в формуле 7.12 к пределу при и используя равенства 7.13 и 7.14, получаем:

7.15

Равенство 7.15 показывает, что касательная составляющая вектора непрерывна при переходе через границу раздела двух сред.

Касательная составляющая вектора , наоборот, претерпевает разрыв, величина которого зависит от соотношения между диэлектрическими проницаемостями. Выражая и в равенстве 7.15 через и , получаем: . 7.16

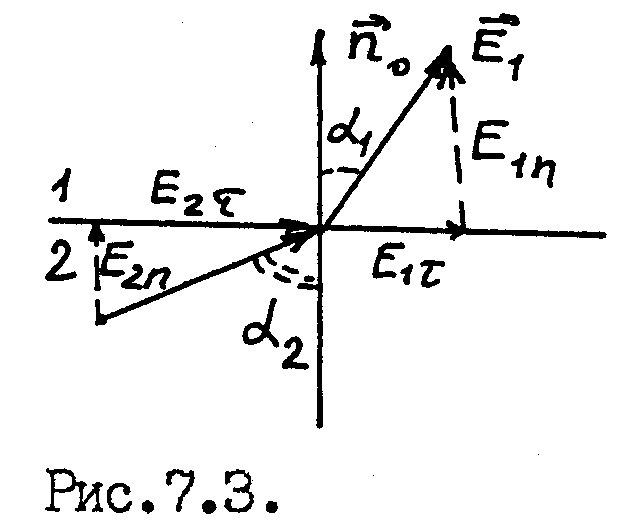
Выведенные граничные условия показывают, что на границе раздела векторы и преломляются. Обозначим углы между нормалью к поверхности раздела и векторами и соответственно через (рис.7.3). Так как , а то, используя граничные условия 7.15 и 7.9, получаем, что при отсутствии поверхностных зарядов на границе раздела спра­ведливо следующее соотношение:

7.17

В изотропных средах векторы и направлены одинаково. Поэтому соотношение 7.17 определяет также и преломление вектора .

Полная система граничных условий. Граничные условия на поверхно­сти идеального проводника

Таким образом, на поверхности раздела двух сред должны выполнятся следующие граничные условия:

. 7.30

, - касательные составляющие векторов, , - нормальные составляющие векторов. Где проекция вектора плотности поверхностных токов на направление N₀. S – поверхность раздела 2-х изотропных сред. P – плоскость проведенная через n₀. n₀ - единичная нормаль проведенная из 2-й среды в 1-ю. ₀ – единичная касательная к отрезку l. l – отрезок на линии пересечеия поверхности пересечения раздела и плоскости Р.

Уравнения 7.30 составляют полную систему граничных условий. Они справедливы для любых электромагнитных процессов, рассматриваемых в макроскопической электродинамике. Не включенные в систему 7.30 гра­ничные условия для составляющих являются следствия­ми соотношений 7.30 и уравнений состояния .

Граничные условия 7.30 можно также записать в векторной форме:

7.31

При изучении переменных электромагнитных полей вблизи поверхности металлических тел часто предполагают, что рассматриваемое тело явля­ется идеально проводящим. При этом граничные условия 7.30 и 7.31 упро­щаются, т.к. в среде с поле отсутствует. Действительно, объем­ная плотность тока проводимости долина быть ограниченной величи­ной. Поэтому из закона Ома 4.20 следует, что напряженность электри­ческого поля внутри идеального проводника должна быть равной нулю. Полагая во втором уравнении Максвелла , получаем . Так как поле считается переменным, то последнее равенство выполняется только при .

Пусть идеально проводящей является вторая среда. Тогда и условия 7.30 принимают вид:

, 7.32

или в векторной форме:

. 7.33

Таким образом, на поверхности идеального проводника касательная составляющая напряженности электрического поля и нормальная сос­тавляющая напряженности магнитного поля обращаются в нуль.