18. Фазовые переходы. Фазовые переходы 1-го рода. Уравнение Клапейрона-Клаузиуса. Фазовые переходы 2-го рода. Уравнение Эренфеста. Критические и закритические явления.

При равновесии, а следовательно, и при фазовых превращениях химические потенциалы вещества в фазах, а также давление (при плоской поверхности) и температура фаз всегда одинаковы. Что же касается других термических и калорических величин (или соответствующих им производных разных порядков от энергии Гиббса), то они при фазовых превращениях теряют непрерывность. Фазовые превращения, при которых скачком изменяется удельный объем v и поглощается (или выделяется) теплота называются фазовыми переходами первого рода. Объем и энтропия выражаются через первые производные энергии Гиббса:

Исходя из этого, Эренфест предложил классификацию фазовых переходов, по ко­торой порядок фазового перехода опреде­ляется порядком тех производных термо­динамического потенциала, которые при переходе испытывают скачки: при фазовых переходах первого рода испытывают скачки (все или только некоторые) первые произ­водные энергии Гиббса, при фазовых пере­ходах второго рода первые производные энергии Гиббса непрерывны, но испытывают скачки его вторые ппоизводные—теплоемкость(С_Р= ), сжимаемость ( ), коэффициент теплового расширения ( ).

В настоящее время известны фазовые переходы первого рода: плавление, кипение, переход проводника из нормального состояния в сверхпроводящее в магнитном поле, переходы из одной кристаллической модификации в другую и т. д., фазовый переход второго рода — превращение проводника из нормального состояния в сверхпроводящее при отсутствии магнитного поля, а также большое число фазовых переходов, при которых вторые производные термодинамического потенциала обращаются в бесконечность (критические переходы): критический переход жидкость —газ, переход ферромагнетика в парамагнетик, сегнетоэлектрический переход и др. Критические переходы не укладываются в классификацию фазовых переходов Эренфеста, указывая на ее ограниченность.

Основным уравнением, характеризующим фазовые переходы пер­вого рода, является дифференциальное уравнение Клапейрона — Клаузиуса. Это уравнение получается из условия равенства хими­ческих потенциалов при равновесии двух фаз и связывает между собой теплоту перехода, скачок удельного объема и наклон кривой равновесия в точке перехода.

Из формулы следует уравнение кривой равновесия р=р(Т). Однако дифференциальное уравнение кривой равновесия имеет нораздо более простой вид и связывает медлу собой указанные выше лекщгко измеряемые величины: . (12.3)

Уравнение является дифференциальным уравнением кривой равновесия и называется уравнением Клапейрона — Клаузиуса. Чаще его записывают в виде: (12.4)

где — теплота перехода на моль или грамм веще­ства; v" — v' — изменение объема соответствующей массы веще­ства. Главное применение уравнения состоит в вычислении удельных теплот испарения, возгонки, плавления и изменения моди­фикации.

Если на систему действует не давление р, а какая-либо другая обобщенная сила А, то мы получаем общее дифференциальное уравнение кривой равновесия двух фаз однокомпонентной системы: .(s – изменение энтропии , а – скачок внешнего параметра).

Уравнением Клапейрона — Клаузиуса: определяет изменение температуры фазового перехода (например, точки замерзания или кипения) с изменением давления.

ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА. УРАВНЕНИЕ ЭРЕНФЕСТА

В отличие от фазовых переходов первого рода при фазовых пере­ходах второго рода никакого скачка в изменении состояния не происходит. Состояние системы изменяется непрерывно, и в точках фазового перехода состояния фаз совпадают. Тепловой эффект перехода равен нулю, и удельный объем остается прежним (s^’’=s^’, v^’’=v^’), но теплоемкость С_р, коэффициент теплового расширения и сжимаемость испытывают скачки. Связь между этими скачками и наклоном кривой равновесия в точке перехода определяется урав­нениями Эренфеста, который впервые (1933) ввел представление о фазовых переходах второго рода при рассмотрении перехода Неl в Неll.

До недавнего времени к фазовым переходам второго рода по­мимо сверхпроводящего перехода при отсутствии магнитного поля относили также превращение железа в точке Кюри в парамагнит­ное состояние, переход Неl в Неll, многие превращения в кристаллах. По современным представлениям, только сверхпроводящий переход при Н = 0 является переходом второго рода по Эренфесту, остальные же из названных переходов имеют другую при­роду.

Найдем уравнения Эренфеста. Правая часть уравнения Кла­пейрона — Клаузиуса (12.3) в точке фазового перехода второго рода принимает вид неопределенности О/О. Для ее раскрытия вос­пользуемся правилом Лопиталя. Дифференцируя числитель и зна­менатель правой части (12.3) или по Т, или по р, получаем уравнения Эренфеста:

В общем случае, если на систему действует обобщенная сила А, которой соответствует внешний параметр а, уравнения Эренфеста будут иметь вид (то же, с заменой р на А, v на а).

Уравнения Эренфеста связывают скачки вторых производных термодинамического потенциала не только при фазовых переходах второго рода, но и в случае целого ряда фазовых переходов первого рода. Примером такого перехода первого рода является переход из упорядоченного состояния в неупорядоченное в сплавах AuCu₃, AuCu и др. Характерной особенностью этих фазовых переходов является постоянство скачков объема и энтропии на всей линии превращения:

, (12.12)

так что на диаграмме Т, р наклон линии фазового равновесия dp/dT= S/ V оказывается постоянным и, следовательно, сама эта линия есть прямая (линейные фазовые переходы первого рода). Дифференцируя уравнение (12.12) по температуре вдоль линии равновесия, получаем выражения откуда непосредственно следуют уравнения Эренфеста.

Таким образом, уравнения Эренфеста определяют широкий класс фазовых превращений — линейные фазовые переходы первого рода и фазовые переходы второго рода.

КРИТИЧЕСКИЕ И ЗАКРИТИЧЕСКИЕ ЯВЛЕНИЯ

В 1860 г. Д. И. Менделеев, исследуя зависимость поверхностного натяжения жидкостей от температуры, установил, что при неко­торой температуре, названной им температурой абсолютного кипения, поверхностное натяжение исчезает. При этом обе сосущест­вующие фазы (жидкость и пар) становятся тождественными. Такое состояние характеризуется определенными значениями темпера­туры Ткр, давления р_кр и объема V_кр и называется критическим состоянием. Кривая равновесия жидкости и пара на диаграмме Т, р кончается в критической точке.

На основании этих экспериментальных исследований Дж. В. Гиббс (1876) и независимо от него А. Г. Столетов (1879) сформулировали основные положения классической термодинами­ческой теории критических явлений. По Гиббсу — Столетову, кри­тическая фаза представляет собой предельный случай двухфаз­ного равновесия, когда обе равновесно сосуществующие фазы ста­новятся тождественными. Иначе говоря, это устойчивое состояние однородной системы, лежащее на границе устойчивости по отно­шению к виртуальным изменениям каждой ее координаты при по­стоянстве других термодинамических сил.

Математически граница устойчивости однородной системы по отношению к таким виртуальным изменениям ее координат опре­деляется обращением в равенства термодинамических неравенств, характеризующих эту устойчивость однородной системы: (dp/dV)_T=0, (dT/dV)_p=0, (dT/dS)_p=0, (dp/dS)_T=0.

Условия устойчивости критического состояния: T S- p V>0.

Критическое состояние определяется четырьмя уравне­ниями для функции двух переменных, не может в данном случае привести к противоречию, так как, согласно термодинами­ческому тождеству

только два из приведенных уравнений являются независимыми.

Критическое состояние системы жидкость — пар — это однокомпонентная, однофазная система, поэтому по правилу фаз n<k число степеней свободы критического состояния f_кр=k-n=0.

Это означает, что критическое состояние простой однокомпонентной системы возможно лишь при определенных температуре, давлении и объеме, т. е. в одной критической точке Т_кр, р_кр, V_кр, Параметры критической точки зависят только от свойств данного вещества.

С изменением термодинамических сил, действующих на систему, изменяются различные характеристики фазового перехода первого рода (ФП I рода). Так, при повышении температуры и давления в системе жидкость — пар уменьшаются удельная теплота пере­хода и области метастабильных и неустойчивых состояний (см. рис. 46). Предельным случаем ФП I рода является критический пе­реход.

Как показывается в статисти­ческой физике, коэффициенты устойчивости обратно пропорцио­нальны флуктуациям различных физических величин. С приближе­нием к критической точке флук­туации растут. За критической точкой существуют только устой­чивые состояния, поэтому в этой области невозможно сосуществование фаз, имеющих границу раздела. Анализ термодинамической устойчивости закритической фазы привел В. К. Семенченко к пост­роению термодинамики непрерывных фазовых переходов.

Как уже упоминалось, рассмотрение изотерм вблизи критиче­ской точки показывает, что точки перегиба на этих изотермах име­ются и в закритической области. Но точка перегиба на кривой соот­ветствует экстремумам на кривых для ее первых производных, В точках квазиспинодали флуктуации достигают при данных усло­виях наибольшего значения и система превращается в смесь флуктуационных зародышей обеих граничных (далеких от этого состоя­ния) фаз — квазифазу или мезофазное состояние*, не теряя своей макроскопической однородности. Поскольку минимум устойчиво­сти является поворотной точкой в отношении изменения свойств фаз, он до некоторой степени аналогичен точке фазового перехода второго рода и условно его можно считать за точку закритического перехода. При этом, конечно, не нужно забывать, что закритический переход происходит на конечном интервале Т, р и других термо­динамических сил. Поэтому в условной точке закритического пере­хода не происходит скачков энтропии, объема и других я,-, а только их быстрое изменение. Работа и удельная теплота перехода также равны по этой причине нулю. Сами коэффициенты устойчивости изменяются также непрерывно, а не скачком; в этом состоит от­личие закритических переходов от ФП II рода по Эренфесту.

До сих пор мы для опреде­ленности пользовались диаграм­мами, относящимися к флюид­ным системам, т. е. системам газ — жидкость. Однако все из­ложенное применимо и к ани­зотропным системам, а также к системам, фазы которых отли­чаются по своим магнитным или электрическим свойствам (ферро-и антиферромагнетики, сверх­проводники и сегнетоэлектрики разных типов).

Очень интерес­ный случай критического перехода в анизотропной среде пред­ставляет а-^-переход в кварце. Он сопровождается резко выражен­ной критической опалесценцией и экстремумами нескольких КУ. Но самым интересным является возможность непосредственного на­блюдения смешанного состояния обеих граничных фаз.

19. Микроканоническое и каноническое распределения Гиббса. Статистический интеграл системы. Энтропия. Большое каноническое распределение (классический и квантовый случай). Термодинамическая эквивалентность канонических распределений.

Рассмотрим многочастичную термодинамически равновесную систему. Основная идея статфизики сос­тоит в замене среднего по времени (b(q, р)); функции b(q, p)

данной системы средним значением b(q, p) этой функции по ан­самблю определенным образом распределенных систем где фазовая плотность распределения p(q, p) для равновесных систем, очевидно, не зависит от времени и удовлетворяет условию нормировки Задача состоит в том, чтобы найти p(q, p), удовлетворяющую равенству Для этого обратимся прежде всего к основному уравнению ста­тистической физики классических систем — уравнению Лнувилля. Из него получаем откуда следует, что равновесная функция распределения p(q, p) является интегралом движения уравнений Гамильтона или функцией интегралов движения: В соответствии с введенным Гиббсом (отвечающим термодина­мике) статистическим определением энтропии (см. ниже) функция p(q, p) зависит лишь от однозначных аддитивных интегралов дви­жения. Известны три таких интеграла движения: энергия Н, им­пульс Р и момент импульса М. Поэтому Для равновесной системы частиц в неподвижном сосуде им­пульс Р и момент импульса М равны нулю. Поэтому в этом слу­чае для систем с заданным числом частиц фазовая плотность рас­пределения зависит лишь от функции Гамильтона Для определения явного вида функции распределения в статис­тической физике принимается в качестве основного положения по­стулат равной априорной вероятности любого микросостояния равновесной изолированной системы, т. е. принимается, что для изолированной системы, имеющей энергию Е с точностью (определяемой заданием макроскопических условий) и число частиц N в объеме V, функция распределения p(q, p) постоянна в слое и равна нулю вне этого слоя:

Равновероятностное распределение микросостояний изолиро­ванной системы называется микроканоническим распределением, а соответствующий ансамбль — микроканоническим ансамблем. С помощью б-функции микроканоническое распределение (12.9) можно записать в виде

П остоянная g(E, N, V) определяется из условия нормировки и имеет смысл плотности распределения фазового объема по энер­гии. Действительно, интеграл от g(E') по допустимым значениям энергии, меньшим Е (Еmin<E'<Е), равен фазовому объему (приведенному), заключенному внутри гиперповерхности Н(q, р) =Е. Увеличение фазового объема Г(Е) при возрастании энергии на величину Е называется статистичес­ким весом макроскопического состояния системы с энергией E и равно где g(E) — энергетическая плотность фазового объ­ема, или, поскольку точки фазового объема изображают состояния, плотность состояний системы с данной энергией Е. Можно показать, что микроканоническое распределение обеспечивает равенство среднего по макроканоническому ансамблю среднему по времени функции координат к импульсов систем. Такие системы называются эргодическими. Обоснование (исходя из механики) эргодичности многочастичных систем и возможности замены средних по времени средними по микроканоническому ансамблю носит название эргодической проблемы. Эта проблема несмотря на ряд полученных важных результатов еще ждет своего решения. Для построения термодинамики многочастичной системы дос­таточно, как известно, определить один из ее термодинамических потенциалов. Остальные величины находятся уже методами самой термодинамики. При независимых макроскопических параметрах E, V, N, которыми определяется термодинамическое состояние рассматриваемой системы, термодинамическим потенциалом явля­ется энтропия. Гиббс определяет ее как величину, пропорциональ­ную логарифму фазового объема где k — универсальная постоянная, равная постоянной Больцмана. Можно показать, что определенная таким образом энтропия обладает известными термодинамическими свойствами.

Заметим, что поскольку при определении энтропии в статис­тическом пределе (N=>, V=>, V/N = v = const) следует учиты­вать только основную асимптотику по числу частиц —N, то опре­деление статистической энтропии не является единствен­ным. Так, например, можно использовать вместо эквива­лентные выражения в виде логарифмов или плотности состояний i статистического веса Логарифмический вид выражений для энтропии обусловлен требованием ее аддитивности, в частности, для невза­имодействующих подсистем. Вычисление фазового объема или ста­тистического веса даже для относительно простых статистических систем .представляют трудную задачу. Поэтому микроканоничес­кое распределение используется в основном не для вычисления термодинамических функций конкретных систем, а для общетеоре­тического рассмотрения. Каноническое распределение Найдем распределение по состояниям (функцию распределения в фазовом пространстве) неизолированной (но замкнутой) систе­мы, находящейся в тепловом контакте с другой системой значи­тельно больших размеров (по числу степеней свободы) — термо­статом. Т — температура термостата и системы, находим каноническое распределение Гиббса

где  — kT называется модулем канонического распределения, а константа A содержит все не зависящие от q и р вели­чины и определяется из условия нормировки Входящий интеграл называется статистич. интегралом системы, а определяемая есть ее энергия Гельмгольца F(T,V,N). Действительно, вычислим внутренние уравнению Гиббса—Гельмгольца т. е. что внутренняя энергия статистической системы равна сред­нему значению ее функции Гамильтона по каноническому распре­делению Гиббса как и должно быть в соответствии с фи­зическим смыслом Е. Поскольку функция Гамильтона системы равна сумме кинетической и потенциальной энергий ее частиц, а кинетическая энергия есть квадратичная функция импульсов, то интегрирова­ние по ним в может быть произведено и мы получим называется конфигурационным интегралом. Интегрирование по импульсам канонического распределения Гиббса легко выполняется и дает конфигурационное рас­пределение Гиббса Энергия Гельмгольца — тепловая длина волны де Бройля. Таким образом вычисление энергии Гельмгольца, а следова­тельно, и всех термодинамических функций многочастичной си­стемы сводится к вычислению ее конфигурационного интеграла (12.24). С помощью известных термодинамических соотношений (5.17) С помощью канонического распределения находим, что энтропия

с истемы пропорциональна среднему значению логарифма плотности веро­ятности, а не является

средним значением какой-либо механиче­ской величины. Большое каноническое распределение Определим теперь распределение по состояниям открытой си­стемы в термостате, называемое большим каноническим распре­делением Гиббса. С такими системами мы встречаемся в целом ряде приложений. Кроме того, использование большого канони­ческого распределения во многих случаях оказывается более эф­фективным, чем микроканонического и канонического распреде­лений. Рассмотрим малую систему, которая находится в тепловом и материальном контакте с термостатом, обмениваясь с ним не только энергией, но и частицами. Границы, отделяющие систему от термостата в некотором смысле условны: они фиксируют лишь ее объем V и другие внешние параметры а, но не энергию Е и число частиц N. В соответствии с этим термодинамическое со­стояние системы определяется переменными Т, V, N. Большое каноническое распределение получим аналогично выводу канонического, исходя из микроканонического распреде­ления для изолированной объединенной (термостат и изучаемая малая система) системы с энергией ЕО и числом частиц NO. От­личие в рассматриваемом случае системы состоит в том, что те­перь следует в явном виде указывать число частиц в ней. Таким образом, подобно функция распределения си­стемы с переменным числом частиц в термостате имеет вид: где индексы о к т относятся соответственно к объединенной си­стеме и к термостату. Поскольку мы будем предполагать, что для энергии E и числа частиц N подсистемы справедливы нера­венства то в первом приближении где учтено, что Подставляя (12.45) в (12.44), находим распределение Гиббса большое каноническое большой статистический интеграл (сумма), большой термодинамический потенциал. Действительно, термодинамические параметры —число частиц и внутренняя энергия —определяемые со­ответствующими частными производными большого термодина­мического потенциала, совпадают со средними значениями числа частиц и функции Гамильтона по большому каноническому рас­пределению Г иббса (12.46).

Термодинамическая эквивалентность канонических распределений Мы рассмотрели три гиббсовских распределения: микрокано­ническое — для изолированных систем, каноническое — для не­изолированных закрытых систем в термостате и большое канони­ческое—для неизолированных открытых систем в термостате.За исключением немногих случаев, использование этих распределений для каждой из названных систем приводит в статистическом преде­ле (N=>, V=>, V/N = u = const) к термодинамически эквива­лентным результатам. Это означает, что каноническим и большим каноническим распределениями можно пользоваться также для описания изолированных систем, что практически является очень важным. Во всех практически важных случаях относительная' флуктуация энергии очень мала и в статистиче­ском пределе стремится к нулю. Малость величины относитель­ной флуктуации означает, что зна­чения энергии системы в термоста­те сколько-нибудь отличные от средней энергии, рактически не­вероятны.

Энергии, заметно отличающиеся от Н, чрезвычайно маловероят­ны, и система ведет себя практически как изолированная. Это и приводит к термодинамической эквивалентности результатов, по­лученных с помощью канонического и микроканонического рас­пределений. Аналогично с помощью большого канонического распределе­ния находим: относительная флуктуация числа частиц в системах большого канонического ансамбля

стремится к нулю в статистическом пределе. Отсюда следует эк­вивалентность большого канонического и канонического распре­делений. Заметим, что, несмотря на термодинамическую эквива­лентность статистических ансамблей, расчеты величины флуктуа­ции, проведенные с их помощью, приводят к различным резуль­татам. Как видно из формулы, относительная флуктуация энергии системы в термостате не будет малой тогда, когда бесконечно большая теплоемкость, и аналогично относительная флуктуация не будет малой при нулевая величина коэффициента устойчивости. Это имеет место, как известно из термодинамики, в критическом состоянии и в двухфазных системах. В этих слу­чаях канонические ансамбли не эквивалентны. основы КВАНТОВОЙ СТАТИСТИКИ Квантовые микроканоническое и каноническое распределения. Определение микроканонического и канонического распреде­лений квантовых систем в целом аналогично рассмотренному классическому случаю. Роль функции распределения играет те­перь статистический оператор р или набор коэффициентов wk. определяющих вероятностное распределение по чистым состоя­ниям.

Как следует из уравнения Неймана, равновесный ста­тистический оператор коммутирует с гамильтонианом И для покоящейся системы является его функцией. Поэтому необходимо задать зависимость коэффициентов wk от энергии Ek.

Если число квантовых состояний изолированной системы, имеющей энергию Е с определенным отклонением Е<Е, равно Г(E), то в соответствии с постулатом равной априорной вероят­ности состояний таких систем имеем квантовое микроканониче­ское распределение 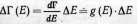из условия нормировки (13.1): 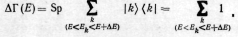а полное число состояний равно Энтропия квантовой статистической системы определяется фор­мулами, Отсюда получаем квантовое канониче­ское распределение по состояниям или после нормировки называется статистической суммой, а есть энергия Гельмгольца квантовой системы, в чем легко убе­диться. Заметим, что каноническое распределение определяет также распределение по энергиям для системы с невырожденными уровнями энергии. При наличии вырождения, когда одному и тому же энергетическому уровню Е соответствует gt различных состояний, вероятность такого вырожденного зна­чения энергии равна Зная энергию Гельмгольца, как функцию своих есте­ственных переменных, все другие термодинамические параметры можно найти методами термодинамики. Энтропия системы равна Таким образом, исследование квантовой статистической системы с помощью канонического распределения сводится к следующей процедуре:

а) вначале решается динамическая задача по определению энергетического спектра Е; и соответствующего набора кванто­вых чисел i путем решения уравнения Шредингера;

б) потом рассчитывается статистическая сумма (13.11) систе­мы и ее энергия Гельмгольца F(Q, V, N) (13.12);в) и далее вычисляются термодинамические характеристики системы. Квантовое большое каноническое распределение. Рассмотрим свойства открытых квантовых систем в термо­стате. Макроскопически такие системы описываются переменны­ми Т, V, N. Границы, отделяющие систему от термостата, прони­цаемы для частиц. Соответствующее этим условиям распределе­ние по состояниям — большое каноническое распределение — мо­жет быть получено подобно каноническому, исходя из микрока­нонического распределения для объединенной изолированной си­стемы с энергией E0 и числом частиц N0. При этом в дополнение к неравенству для энергии системы необходимо добавить неравенство для числа ее ча­стиц Отсюда, используя микроканоннческое распределение для объ­единенной системы, находим большое каноническое распределе­ние по состояниям i квантовой открытой системы а термо­стате:

большой термодинамический потенциал. Действительно, вычисленные с помощью (13.19) по формулам термодинамики энергия и число частиц системы равны соответ­ствующим средним по большому каноническому распределению: Энтропия системы, как и в случае канонического распределения определяется средним значением логарифма функции распреде­ления: Таким образом, при использовании большого канонического распределения для исследования квантовых статистических систем необходимо прежде всего определить энергетический спектр системы из решения уравнения Шредингера Причем в отличие от канонического распределения требуется най­ти зависимость спектра для произвольного числа частиц N, в том числе и для малых N~ 1. Затем следует расчет большой статистической суммы и большого термодинамического потенциала . Далее методами термодинамики вычисляются все необходимые термодинамические характеристики системы.

20. Статистическая термодинамика квантовых идеальных одноатомных газов. Распределение Бозе-Эйнштейна и Ферми-Дирака. Сопоставление распределений М.-Б., Б.-Э. и Ф.-Д. Вырождение квантовых газов. Теплоёмкость твёрдых тел.

При температурах Т<Т₀ ( ) система частиц становится квантовой. Квантовые частицы помимо волновых свойств обладают собственным (спиновым) механическим моментом. Его величина равна h ,где спин s – целое (включая нуль) или полуцелое положительное число, определяемое природой частиц. Таким образом, состояние квантовой частицы данного типа определяется волновой функцией Ψ(x,y,z) и спиновым числом m_s (характеризующим одно из возможных значений проекций спинового момента на фиксированную ось). Возможны 2s+1 состояний с заданной волновой функцией, отличающейся ориентацией спина.

Так как в отсутствие магнитного поля энергия частицы не зависит от ориентации спина, то наличие спина увеличивает число квантовых состояний с заданной энергией в 2s+1 раз. В зависимости от того, является ли спин целым или полуцелым, частицы делятся на два класса: бозе-частицы, или бозоны (с целым спином), и ферми-частицы, или фермионы (с полуцелым спином). Бозонами являются фотон (s=1), π- и К-мезоны (s=0). Большинство элементарных частиц (электроны, протоны, нейтроны и др.) имеют спин s = и являются фермионами.

Спин сложной частицы определяется числом входящих в нее фермионов. Если это число четное (Н, Н₂, Не⁴), то сложная частица является бозоном, если нечетное (D, HD) – фермионом.

Волновая функция системы бозонов симметрична, а фермионов – антисимметрична относительно перестановки любой пары частиц. Волновая функция квантового идеального газа представляется произведением волновых функций отдельных частиц и полностью определяется заданием чисел заполнения n_k каждого к-го одночастичного состояния. Требование антисимметрии волновой функции системы фермионов приводит к тому, что они удовлетворяют принципу Паули: в заданном квантовом состоянии может находиться не более одной частицы, т.е. n_k=0; 1. В каждом одночастичном состоянии бозе-газа может находиться любое число частиц: n_k=0;1;2,…N, где N – общее число частиц в системе.

Распределение частиц по одночастичным квантовым состояниям зависит от того, являются ли частицы бозонами или фермионами. В соответствии с этим существуют две квантовые статистики: статистика Бозе-Эйнштейна (для бозонов) и статистика Ферми-Дирака (для фермионов). Функция распределения по квантовым состояниям обоих классов частиц имеет вид:

= (n_k) = ^k / ^k 1. Распределение бозе-частиц по состояниям называется распределением Бозе-Эйнштейна: = оно было установлено в 1924 г. Распределение частиц по энергиям найдем, умножив на число g_k микросостояний с энергией : ( ) = 2. Распределение Ферми-Дирака Среднее число ферми-частиц в к-ом состоянии равно: = Распределение электронов по эгеогиям (s= ) будет ( ) = сопоставление распределений М-Б, Б-Э и Ф-Д: все эти три функции распределения идеальных газов можно записать в едином виде: = , (1) где для распределения М-Б, для распределения Ф-Д, для распределения Б-Э. На рис приведены графики этих функций распределения. Из (1 ) видно, что распределения Б-Э и Ф-Д переходят в распределение М-Б, т.е. газ становится классическим, если . (2) Если , то функция распределения газа отличается от максвелл-больщмановской и говорят, что газ вырожден. Величина называется фактором вырождения, выражение (2) – критерием невырожденности, а противоположные неравенства – критерием сильного вырождения.

Теплоемкость твердых тел рассчитывается по формуле Дюлонга и Пти: Твердое тело рассматривается как совокупность N независимых атомов, колеблющихся с одной и той же частотой ν. Однако средняя энергия, приходящаяся на одну степень свободы, полагается равной не КТ, а вычисляется по формуле Планка для средней энергии линейного осциллятора: (1)энергия грамм-атома, имеющего 3N степеней свободы, равна: (2), величину , имеющего размерность температуры, Эйнштейн назвал характеристической температурой тела. Следовательно , дифференцируя по температуре, получим

При низких температурах (Т<<θ), , вследствие чего единицей в знаменателе можно пренебречь и записать: При Т , а