13. Общие свойства решений одномерного уравнения Шрёдингера. Частица в прямоугольной потенциальной яме бесконечной и конечной "глубины". Спектр энергии и собственные функции.

(1) – общий вид уравнения Шредингера, где

(2) – оператор Гамильтона

(3) – одномерное уравнение Шредингера или уравнение Шредингера для стационарных состояний. Это уравнение не содержит времени.

Шредингер показал, что уравнение (3) полностью решает проблему квантования энергии системы. Квантование энергии возникает потому. Что на волновые функции, являющиеся решениями уравнения Шредингера, накладываются определенные естественные ограничения. При этих ограничениях уравнение (3) имеет решения не при всех, а только при избранных значениях параметра Е. Естественные ограничения состоят в том, что волновая функция и ее первые пространственные производные должны быть конечны, однозначны и непрерывны даже в точках разрыва потенциальной функции . Избранные значения параметра Е, для которых уравнение (3) имеет решения, удовлетворяющие перечисленным ограничениям, называются собственными значениями величины Е для диф. уравнения (3), соответствующие им решения – собственными функциями того же уравнения Собственные значения Е и принимаются за возможные значения энергии в стационарных состояниях. Совокупность возможных значений величины Е называются спектром этой величины. Собственные значения могут быть дискретными, а могут непрерывно заполнять конечный или бесконечный интервал. Получаем дискретный и непрерывный спектры энергии.

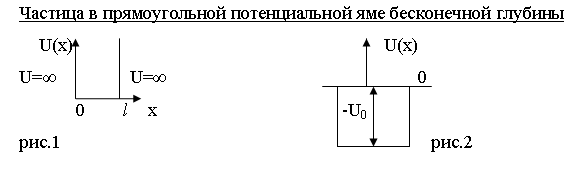
Предположим, частица может двигаться лишь вдоль оси x. Пусть движение ограничено непроницаемыми для частицы стенками: x=0 и x=l Потенциальная энергия в этом случае имеет след.вид (рис.1): она равна нулю при 0≤x≤ l и обращается в бесконечность за пределами этого интервала.

За пределы потенциальной ямы частица попасть не может, следовательно, функция за пределами ямы равна нулю. Из условия непрерывности следует, что должна быть равна нулю и на границах ямы: . В области, где не равна тождественно нулю. Уравнение Шредингера можно записать так: . Решив его, найдем собственные функции и собственные значения задачи. Собственные значения энергии частицы: (4)

Отсюда видно, что энергия квантуется. Энергетические спектры дискретны, при U₀=+∞ число их бесконечно велико. Т.к. значение n=0 исключается, то энергия наинизшего уровня равна . Это нулевая энергия, необходимость которой следует из общих положений.

Собственные функции задачи: (5)

Частица в прямоугольной яме конечной глубины.

Потенциальную функцию вне ямы U(x) примем равной нулю. Внутри ямы U(x)=U₀<0. За начало координат возьмем центр ямы 0. (рис.2). Исследуем сначала случай, когда полная энергия Е отрицательна, причем U₀<E<0. Введем обозначения (6)

Тогда уравнение Шредингера внутри ямы будет: (7), а вне ямы: (8). Общее решение (7) имеет вид (9). Решение уравнения (8): при x>a и при x<-a . Все возможные решения разделяются на два класса: 1) с четной волновой функцией, когда A≠0, B=0 и C=D, k*ctg(ka)=a (10)

2) c нечетной волновой функцией, когда A=0, B≠0,C=-D, k*ctg(ka)=-a(11).

Уровни энергии найдутся путем графического или численного решения (10) или (11), в которых положительные величины определяются выражениями (6). Т.к. k существенно отлична от нуля, то из (6) следует, что E>U₀. Все уровни энергии, в том числе и самый низший, лежат выше дна потенциальной ямы. Опять наше решение приводит к необходимости существования нулевой энергии. Теперь рассмотрим случай, когда Е>0. в этом случае величина a чисто мнимая. Вместо (8) получаем уравнение (8а) Его решения: при x>+a, при x<-a. Оба решения остаются конечными при любых значениях х, в частности сколь угодно больших по абсолютной величине. Эти решения надо сшить с решением внутри интервала –a<x<+a, которое представляется формулой (9). Таким путем, получается 4 линейных уравнения относительно , содержащие А и В в качестве параметров. Этого достаточно, чтобы выразить эти неизвестные коэффициенты через А и В. При этом А и В могут принимать любые значения. Отсюда следует, что при Е>0 энергия не квантуется – спектр непрерывен. Волновая функция не стремится к нулю при , т.е. движение частицы инфинитно, как того и требует общая теория.