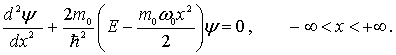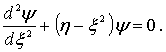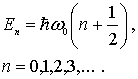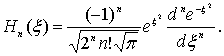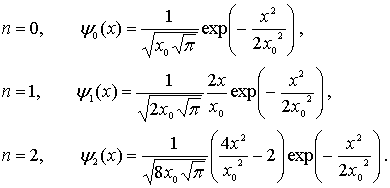- •1. Уравнение Лагранжа примеры его составления. Функция Лагранжа, ее свойства.
- •Свойства функции Лагранжа
- •2. Законы сохранения, соответствующие фундаментальным симметриям: энергия, импульс, момент импульса.
- •В общем случае теорема об изменении обобщенной энергии имеет вид
- •3. Канонические уравнения Гамильтона. Первые интегралы уравнений Гамильтона. Эквивалентность лагранжевого и гамильтонового формализма.
- •4. Движение в центральных полях. Кеплерова задача. Параметрическое уравнение. Траектории движения.
- •5. Уравнения Максвелла.
- •6. Проводники и диэлектрики.
- •7. Граничные условия для векторов электрического поля.
- •7.3. Условия для касательных составляющих векторов и
- •8. Граничные условия для векторов магнитного поля
- •9. Скалярный и векторный потенциалы заряда, движущегося с постоянной скоростью; формула Лоренца.
- •10. Преобразования Лоренца для проекций векторов и . Инварианты электромагнитного поля.
- •11. Полное описание квантовой системы. Принцип суперпозиции. Ортогональность и нормировка собственных функций эрмитовых операторов. Базис пространства состояний. Чистые и смешанные состояния.
- •13. Общие свойства решений одномерного уравнения Шрёдингера. Частица в прямоугольной потенциальной яме бесконечной и конечной "глубины". Спектр энергии и собственные функции.
- •14. Квантовое движение в центральном поле. Состояния электрона в поле ядра. Атом водорода и водородоподобные ионы. Квантовые числа.
- •15. Гармонический осциллятор в энергетическом представлении. Операторы рождения и уничтожения. Спектр энергии и собственные функции.
- •Общие условия равновесия и устойчивости
- •Равновесие гомогенной системы
- •18. Фазовые переходы. Фазовые переходы 1-го рода. Уравнение Клапейрона-Клаузиуса. Фазовые переходы 2-го рода. Уравнение Эренфеста. Критические и закритические явления.
15. Гармонический осциллятор в энергетическом представлении. Операторы рождения и уничтожения. Спектр энергии и собственные функции.
Квантовый гармонический
осциллятор.гармоническим осциллятором
называется система, способная совершать
гармонические колебания. Рассмотрим
одномерный гармонический осциллятор,
совершающий колебания вдоль оси
![]() под
действием возвращающей квазиупругой
силы
под
действием возвращающей квазиупругой
силы
![]() .
Потенциальная энергия такого осциллятора
имеет вид
.
Потенциальная энергия такого осциллятора
имеет вид
|
(4.77) |
Рис. 4.24. |
(4.78) |
Вводя величины
|
(4.79) |
и переходя к новой
безразмерной переменной
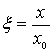 ,
приводим уравнение (4.78)
к виду
,
приводим уравнение (4.78)
к виду
|
(4.80) |
Анализ показывает, что
волновые функции, являющиеся решением
уравнения (4.80)
, будут непрерывными и конечными не при
всех значениях параметра
![]() ,
а лишь при
,
а лишь при
![]() Выражая,
согласно (4.79),
энергию осциллятора
Выражая,
согласно (4.79),
энергию осциллятора
![]() через
,
получаем
через
,
получаем
|
(4.81) |
Это соотношение и
определяет закон квантования энергии
гармонического осциллятора. Отметим,
что энергетические уровни гармонического
осциллятора, в отличие, например, от
случая прямоугольной потенциальной
ямы, являются эквидистантными,
т.е. расположены на одинаковом
энергетическом расстоянии
![]() друг
от друга (рис.4.25) .
друг
от друга (рис.4.25) .
Рис.4.25.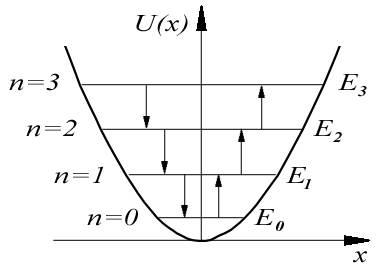
![]() ,
соответствующих значению квантового
числа
,
соответствующих значению квантового
числа![]() .
Отличие от нуля минимальной энергии
осциллятора характерно, как мы уже
видели, для всех квантовых систем и
является следствием соотношения
неопределенностей. значение нулевой
энергии
.
Отличие от нуля минимальной энергии
осциллятора характерно, как мы уже
видели, для всех квантовых систем и
является следствием соотношения
неопределенностей. значение нулевой
энергии
![]() есть
минимальное значение энергии осциллятора,
которое согласуется с требованиями
соотношения неопределенностей. Поместим
начало координат в точку, являющуюся
положением равновесия гармонического
осциллятора, совершающего колебания
по закону
есть
минимальное значение энергии осциллятора,
которое согласуется с требованиями
соотношения неопределенностей. Поместим
начало координат в точку, являющуюся
положением равновесия гармонического
осциллятора, совершающего колебания
по закону
![]() .
Тогда неопределенность координаты
.
Тогда неопределенность координаты
![]() принимает
вид
принимает
вид
 Амплитуда
колебаний
связана
с энергией
Амплитуда
колебаний
связана
с энергией
![]() соотношением
соотношением
![]() ,
следовательно
,
следовательно
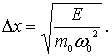 Аналогично,
для неопределенности импульса имеем
Аналогично,
для неопределенности импульса имеем
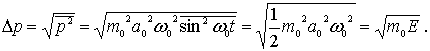 Подставляя
Подставляя
![]() и
и
![]() в
соотношение неопределенностей
в
соотношение неопределенностей
![]() ,
получаем следующее условие
,
получаем следующее условие
![]() т.е.
действительно, минимальное значение
энергии гармонического осциллятора
есть
т.е.
действительно, минимальное значение
энергии гармонического осциллятора
есть
![]() .
Эквидистантность
энергетических уровней гармонического
осциллятора (4.83)
на первый взгляд означает, что осциллятор
может поглощать и испускать излучение
с частотой
.
Эквидистантность
энергетических уровней гармонического
осциллятора (4.83)
на первый взгляд означает, что осциллятор
может поглощать и испускать излучение
с частотой
![]() ,
кратной
,
кратной
![]() ,
т.е.
,
т.е.
![]() ,
где
,
где
![]() -
разность квантовых чисел начального и
конечного уровней осциллятора. Однако,
на самом деле это не так. Точный расчет,
выходящий за рамки данного курса,
показывает, что особенности испускания
и поглощения электромагнитного излучения
гармоническим осциллятором таковы, что
возможны переходы только между соседними
уровнями, т.е.
-
разность квантовых чисел начального и
конечного уровней осциллятора. Однако,
на самом деле это не так. Точный расчет,
выходящий за рамки данного курса,
показывает, что особенности испускания
и поглощения электромагнитного излучения
гармоническим осциллятором таковы, что
возможны переходы только между соседними
уровнями, т.е.
|
(4.82) |
Условия, которые определяют изменение квантовых чисел при разрешенных переходах системы из одного состояния в другое, называются правилами отбора. Таким образом, правила отбора, характеризующие испускание и поглощение электромагнитного излучения гармоническим осциллятором, имеют вид (4.82) . Перейдем теперь к анализу волновых функций гармонического осциллятора. Как показано в теории дифференциальных уравнений с переменными коэффициентами, волновые функции, являющиеся решениями уравнения (4.80) , имеют вид
|
(4.83) |
где
![]() -
полином Чебышева-Эрмита
-
полином Чебышева-Эрмита
![]() -го
порядка, определяемый выражением
-го
порядка, определяемый выражением
|
(4.84) |
Отметим, что для этих
полиномов справедливо рекуррентное
соотношение
![]() позволяющее
найти
позволяющее
найти
![]() для
всех
для
всех
![]() ,
зная
,
зная
![]() и
и
![]() .
Например,
.
Например,
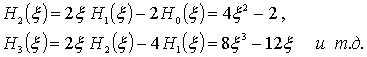 Волновые
функции (4.83)
ортонормированы, т.е. удовлетворяют
условию
Волновые
функции (4.83)
ортонормированы, т.е. удовлетворяют
условию
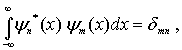 где
где
![]() -
символ Кронекера (4.18)
. Приведем вид волновых
функций для первых трех энергетических
уровней гармонического осциллятора
-
символ Кронекера (4.18)
. Приведем вид волновых
функций для первых трех энергетических
уровней гармонического осциллятора
|
(4.85) |
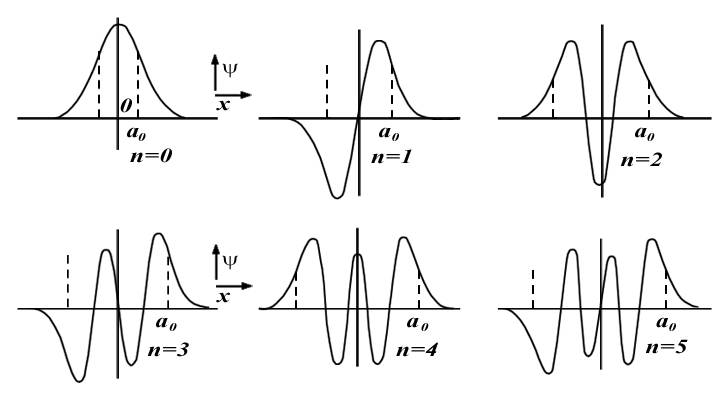
Графики волновых функций для значений квантового числа от 0 до 5 представлены на рис.4.26. Отрезок определяет область, в
|
Рис. 4.26. |
которой совершал бы
колебания классический осциллятор.
Ширина этой области оказывается различной
для разных значений квантового числа
,
поскольку энергия осциллятора, а,
следовательно, и амплитуда его колебаний
также зависят от
.
Из (4.83)
- (4.85)
следует, что волновые функции гармонического
осциллятора обладают определенной
четностью. Они являются четными функциями
координаты
при
четных значениях
и
при
,
и нечетными функциями при нечетных
.
Значение квантового числа
определяет
также число точек пересечения волновой
функции с осью
.
В основном состоянии, т.е. при
![]() ,
точки пересечения внутри параболической
ямы отсутствуют, при
,
точки пересечения внутри параболической
ямы отсутствуют, при
![]() имеется
одна точка пересечения, при
имеется
одна точка пересечения, при
![]() -
две и так далее. Таким образом, при
увеличении квантового числа
на
единицу волновая функция гармонического
осциллятора меняет четность и приобретает
добавочную точку пересечения с осью
-
две и так далее. Таким образом, при
увеличении квантового числа
на
единицу волновая функция гармонического
осциллятора меняет четность и приобретает
добавочную точку пересечения с осью
![]() .
Отметим, что вне
классической области
.
Отметим, что вне
классической области
![]() волновые
функции
волновые
функции
![]() отличны
от нуля, что свидетельствует о том, что
квантовый гармонический осциллятор с
определенной вероятностью может
находиться вне пределов параболической
потенциальной ямы. В задаче 4.10 выполнен
расчет вероятности пребывания частицы
вне классической области для гармонического
осциллятора, находящегося в основном
состоянии. При малых
значениях квантового числа
плотность
вероятности нахождения частицы,
определяемая квадратом модуля волновой
функции
отличны
от нуля, что свидетельствует о том, что
квантовый гармонический осциллятор с
определенной вероятностью может
находиться вне пределов параболической
потенциальной ямы. В задаче 4.10 выполнен
расчет вероятности пребывания частицы
вне классической области для гармонического
осциллятора, находящегося в основном
состоянии. При малых
значениях квантового числа
плотность
вероятности нахождения частицы,
определяемая квадратом модуля волновой
функции
![]() ,
кардинальным образом отличается от
плотности вероятности обнаружения
классического осциллятора
,
кардинальным образом отличается от
плотности вероятности обнаружения
классического осциллятора
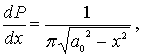 (4.86)
изображенной на рис.4.27 пунктирными
линиями. Так, при
(4.86)
изображенной на рис.4.27 пунктирными
линиями. Так, при
![]() имеет
форму гауссовской кривой с
имеет
форму гауссовской кривой с
м
Рис. 4.27.
![]() ,
тогда как плотность вероятности
обнаружения классического осциллятора
(4.86)
наоборот минимальна в точке
,
тогда как плотность вероятности
обнаружения классического осциллятора
(4.86)
наоборот минимальна в точке
![]() и
стремится к
и
стремится к
![]() в
точках поворота, в которых скорость
частицы обращается в нуль (рис.4.27а).
При значительной
величине квантового числа
,
например, при
в
точках поворота, в которых скорость
частицы обращается в нуль (рис.4.27а).
При значительной
величине квантового числа
,
например, при
![]() функция
приближается
к классической кривой распределения.
Она достигает максимума вблизи точек
поворота и резко спадает вне классической
области движения (рис.4.27б) . При
функция
приближается
к классической кривой распределения.
Она достигает максимума вблизи точек
поворота и резко спадает вне классической
области движения (рис.4.27б) . При
![]() кривая
вероятности
,
как того и требует принцип соответствия,
переходит в классическую функцию
распределения плотности
вероятности. Отметим,
что модель гармонического осциллятора
и связанная с ним задача о движении
частицы в параболической потенциальной
яме является идеализацией, справедливой
лишь при малых отклонениях колеблющейся
частицы от положения равновесия. Во
всех реальных ситуациях потенциальная
энергия
кривая
вероятности
,
как того и требует принцип соответствия,
переходит в классическую функцию
распределения плотности
вероятности. Отметим,
что модель гармонического осциллятора
и связанная с ним задача о движении
частицы в параболической потенциальной
яме является идеализацией, справедливой
лишь при малых отклонениях колеблющейся
частицы от положения равновесия. Во
всех реальных ситуациях потенциальная
энергия
![]() частицы,
совершающей колебания около положения
равновесия, имеет более сложный по
сравнению с (4.79)
вид. Поэтому при возрастании амплитуды
колебаний, начиная с некоторых значений
амплитуд, движение частицы будет все
больше отличаться от гармонических
колебаний. Такое движение называют
ангармоническим движением, а соответствующий
осциллятор - ангармоническим
осциллятором. Однако в случае малых
колебаний влияние ангармонизма ничтожно
мало, что позволяет использовать модель
гармонического осциллятора для описания
колебательного движения квантово-механических
систем. Выполненный в
данной главе анализ движения частиц в
прямоугольной и параболической
потенциальных ямах показывает, что не
смотря на отличие в форме ямы, в поведении
частицы в яме имеется много общего: 1.
Энергетический спектр частицы, находящейся
в яме, является дискретным, т.е. энергия
частицы квантуется. 2.
Частица, находящаяся в основном состоянии,
т.е. на самом низшем энергетическом
уровне, обладает не равной нулю
энергией. 3. Плотность
вероятности нахождения частицы
частицы,
совершающей колебания около положения
равновесия, имеет более сложный по
сравнению с (4.79)
вид. Поэтому при возрастании амплитуды
колебаний, начиная с некоторых значений
амплитуд, движение частицы будет все
больше отличаться от гармонических
колебаний. Такое движение называют
ангармоническим движением, а соответствующий
осциллятор - ангармоническим
осциллятором. Однако в случае малых
колебаний влияние ангармонизма ничтожно
мало, что позволяет использовать модель
гармонического осциллятора для описания
колебательного движения квантово-механических
систем. Выполненный в
данной главе анализ движения частиц в
прямоугольной и параболической
потенциальных ямах показывает, что не
смотря на отличие в форме ямы, в поведении
частицы в яме имеется много общего: 1.
Энергетический спектр частицы, находящейся
в яме, является дискретным, т.е. энергия
частицы квантуется. 2.
Частица, находящаяся в основном состоянии,
т.е. на самом низшем энергетическом
уровне, обладает не равной нулю
энергией. 3. Плотность
вероятности нахождения частицы
![]() имеет
максимумы в области между классическими
точками поворота и экспоненциально
спадает вне классической области. Это
означает, что с определенной вероятностью
частица может находиться вне ямы (за
исключением ям с бесконечно высокими,
непроницаемыми, стенками). 4.
При увеличении квантового числа
на
единицу волновая функция, описывающая
поведение частицы в яме, приобретает
дополнительную точку пересечения с
осью
.
Подчеркнем, что отмеченные
свойства не зависят от формы потенциальной
ямы, т.е. от вида потенциальной энергии
. Следует
отметить еще одно важное обстоятельство:
энергетический спектр частицы является
дискретным (энергия квантуется) только
в тех случаях, когда частица находится
в потенциальной яме. Если же частица
движется в области потенциального
порога, барьера, или над потенциальной
ямой ( при
имеет
максимумы в области между классическими
точками поворота и экспоненциально
спадает вне классической области. Это
означает, что с определенной вероятностью
частица может находиться вне ямы (за
исключением ям с бесконечно высокими,
непроницаемыми, стенками). 4.
При увеличении квантового числа
на
единицу волновая функция, описывающая
поведение частицы в яме, приобретает
дополнительную точку пересечения с
осью
.
Подчеркнем, что отмеченные
свойства не зависят от формы потенциальной
ямы, т.е. от вида потенциальной энергии
. Следует
отметить еще одно важное обстоятельство:
энергетический спектр частицы является
дискретным (энергия квантуется) только
в тех случаях, когда частица находится
в потенциальной яме. Если же частица
движется в области потенциального
порога, барьера, или над потенциальной
ямой ( при
![]() )
, то ее энергетический спектр является
непрерывным (квантование отсутствует).
Этот результат согласуется с общей
теоремой квантовой механики, согласно
которой энергия всегда квантуется у
систем, которые не могут уходить на
бесконечность, и не квантуется у систем,
способных уходить на бесконечность.
Задача 4.10. Гармонический
осциллятор находится в основном
состоянии. Найдите вероятность обнаружения
частицы вне пределов классической
области, т.е. вне области
)
, то ее энергетический спектр является
непрерывным (квантование отсутствует).
Этот результат согласуется с общей
теоремой квантовой механики, согласно
которой энергия всегда квантуется у
систем, которые не могут уходить на
бесконечность, и не квантуется у систем,
способных уходить на бесконечность.
Задача 4.10. Гармонический
осциллятор находится в основном
состоянии. Найдите вероятность обнаружения
частицы вне пределов классической
области, т.е. вне области
![]() ,
где
-
амплитуда классических колебаний.
Решение: Поскольку
осциллятор находится в основном
состоянии, то, согласно (4.81)
, (4.83)
его энергия равна
,
где
-
амплитуда классических колебаний.
Решение: Поскольку
осциллятор находится в основном
состоянии, то, согласно (4.81)
, (4.83)
его энергия равна
![]() ,
а волновая функция, описывающая его
состояние, имеет вид
,
а волновая функция, описывающая его
состояние, имеет вид
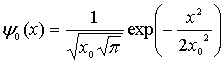 .
Здесь
-
частота классического гармонического
осциллятора, а параметр
.
Здесь
-
частота классического гармонического
осциллятора, а параметр
![]() определяется
выражением
определяется
выражением
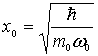 . При
максимальном отклонении классического
осциллятора от положения равновесия
его полная энергия должна быть равна
потенциальной энергии, т.е.
. При
максимальном отклонении классического
осциллятора от положения равновесия
его полная энергия должна быть равна
потенциальной энергии, т.е.
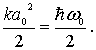 Отсюда
следует, что амплитуда классических
колебаний
Отсюда
следует, что амплитуда классических
колебаний
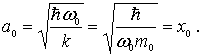 Найдем
вероятность обнаружения частицы в
классической области
Найдем
вероятность обнаружения частицы в
классической области
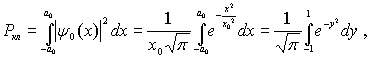 где
где
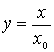 .
Поскольку под интегралом стоит четная
функция переменной
.
Поскольку под интегралом стоит четная
функция переменной
![]() ,
то
,
то
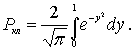 Интеграл
Интеграл
 называется
интегралом вероятностей . Этот интеграл
широко используется в теории вероятностей,
статистике, теоретической и математической
физике, его значения для различных
пределов интегрирования
называется
интегралом вероятностей . Этот интеграл
широко используется в теории вероятностей,
статистике, теоретической и математической
физике, его значения для различных
пределов интегрирования
![]() приведены
в таблицах. В данном случае, при
приведены
в таблицах. В данном случае, при
![]() ,
,
![]() ,
следовательно
,
следовательно
![]() Соответственно,
вероятность
Соответственно,
вероятность
![]() того,
что частица будет обнаружена вне
классической области, равна
того,
что частица будет обнаружена вне
классической области, равна
![]() Таким
образом, вероятность пребывания
гармонического осциллятора, находящегося
в основном состоянии, вне пределов
классической области составляет ~ 16 %,
т.е. имеет заметную величину.
Таким
образом, вероятность пребывания
гармонического осциллятора, находящегося
в основном состоянии, вне пределов
классической области составляет ~ 16 %,
т.е. имеет заметную величину.
16. Основные законы и методы термодинамики. Три начала термодинамики. Энтропия и термодинамическая температура. Метод круговых процессов, метод термодинамических потенциалов. Термодинамические потенциалы сложных систем и систем с переменным числом частиц.
Первый постулат. У изолированной системы существует состояние термодинамического равновесия, в которые она приходит с течением времени и выйти из которого сама не может. Второй. Все равновесные внутренние параметры системы (величины, определяющиеся совокупным движением и распределением в пространстве входящих в систему частиц: р, Е) являются функциями внешних параметров (величины, входящие в систему: V) и температуры.
Первое начало ТД. Выражает закон сохранения и превращения энергии. Внутренняя энергия системы является однозначной функцией её состояния и изменяется только под влиянием внешних воздействий. Другая формулировка: невозможен вечный двигатель первого рода (совершающий работу, не заимствуя энергию извне).
Второе начало. Невозможен вечный двигатель второго рода (устройство, полностью превращающее теплоту в работу).
Третье начало. По мере приближения температуры к нулю, энтропия всякой равновесной системы при изотермических процессах перестает зависеть от каких-либо термодинамических параметров состояния и в пределе при температуре, стремящейся к 0К, принимает одну и ту же для всех систем постоянную величину, которую можно принять равной нулю.
Методы термодинамики. Метод циклов:
![]() (первое
начало)
(первое
начало)
![]()
Метод термодинамических потенциалов:![]() ,
где Аi и ai
– сопряжённые обобщённые термодинамические
сила и параметр (p и V).
,
где Аi и ai
– сопряжённые обобщённые термодинамические
сила и параметр (p и V).
Термодинамические потенциалы: U(S,V), F(T,V) = U - TS, G(T, p) = U – TS + pV, H(S,p) = U + pV. Зная хотя бы одну характеристическую функцию, можно вычислить параметры всей системы. Первые производные характеристических функций дают параметры системы. Через вторые производные можно выразить калорические свойства системы, т. е. теплоёмкость.
Термодинамические потенциалы систем
с постоянным числом частиц. Для
открытой системы с учётом химического
превращения частиц:![]() ,
где
,
где
![]() внутр.
+
внутр.
+
![]() обмен
с вн. средой,
обмен
с вн. средой,
![]() - химический потенциал k-ой
частицы. При равновесных химических
процессах
- химический потенциал k-ой
частицы. При равновесных химических
процессах
![]() - основное уравнение термодинамики для
систем с постоянным числом частиц.
- основное уравнение термодинамики для
систем с постоянным числом частиц.
![]() - это химический потенциал, значение
энергии Гиббса на одну частицу. Он не
зависит от числа частиц, зависит только
от T и p. Если в системе смесь веществ, то
- это химический потенциал, значение
энергии Гиббса на одну частицу. Он не
зависит от числа частиц, зависит только
от T и p. Если в системе смесь веществ, то
![]() .
.
17. Равновесные процессы. Основное уравнение термодинамики для равновесных процессов. Условия термодинамического равновесия и устойчивости. Условия устойчивости равновесия однородной системы. Равновесие в гомогенной системе. Условия химического равновесия.
Если некоторые параметры системы
изменяются со временем, то говорят, что
в ней происходит процесс.
По первому постулату ТД всякая система,
выведенная из состояния равновесия, с
течением времени вернется в какое-либо
равновесие. Процесс перехода системы
из неравновесного состояния в равновесное
называется релаксацией,
а время установления равновесного
состояния называется временем релаксации
![]() .
Строго говоря, такое определение времени
релаксации не является однозначным,
так как зависит от способа вывода системы
из состояния равновесия, поэтому чаще
под временем
релаксации понимают время, за
которое отклонение параметра уменьшается
в e=2.71 раза. Это обусловлено
тем, что по мере приближения к равновесному
значению, зависимость отклонения
параметра от равновесного носит
экспоненциальный характер.
.
Строго говоря, такое определение времени
релаксации не является однозначным,
так как зависит от способа вывода системы
из состояния равновесия, поэтому чаще
под временем
релаксации понимают время, за
которое отклонение параметра уменьшается
в e=2.71 раза. Это обусловлено
тем, что по мере приближения к равновесному
значению, зависимость отклонения
параметра от равновесного носит
экспоненциальный характер.
С понятием времени релаксации тесно
связано определение равновесных
процессов. Процесс называется
квазистатическим
или равновесным,
если все параметры системы изменяются
бесконечно медленно, так что система
всё время фактически находится в
равновесных состояниях. Это возможно
в случае, когда
![]()
Обратимым называется процесс, если возвращение системы в исходное состояние можно осуществить без каких-либо изменений в окружающих телах. Всякий квазистатический процесс обратим. Примерами необратимых процессов являются: процесс теплопередачи при конечной разности температур, расширение газа в пустоту, процесс диффузии.
Основное уравнение термодинамики
Согласно
второму началу термодинамики, элементарное
количество теплоты
![]() связано
с изменением энтропии системы
связано
с изменением энтропии системы
![]() следующим
неравенством (см. формулу (3.59)):
следующим
неравенством (см. формулу (3.59)):
![]() .(4.1) Совместно
с первым началом термодинамики
.(4.1) Совместно
с первым началом термодинамики
![]() ,
(4.2) выражение (4.1)
дает основное
неравенство термодинамики
в
виде:
,
(4.2) выражение (4.1)
дает основное
неравенство термодинамики
в
виде:
![]() .
(4.3) В этом выражении
знак равенства соответствует равновесным
термодинамическим процессам, а знак
неравенства - неравновесным. Для
анализа равновесных процессов выражение
(4.3)
может быть записано в виде уравнения
.
(4.3) В этом выражении
знак равенства соответствует равновесным
термодинамическим процессам, а знак
неравенства - неравновесным. Для
анализа равновесных процессов выражение
(4.3)
может быть записано в виде уравнения
![]() ,
(4.4) которое носит название основного
уравнения термодинамики равновесных
(обратимых) процессов.
Уравнение (4.4)
позволяет проводить расчет любых
равновесных термодинамических процессов.
,
(4.4) которое носит название основного
уравнения термодинамики равновесных
(обратимых) процессов.
Уравнение (4.4)
позволяет проводить расчет любых
равновесных термодинамических процессов.
Рассмотрим применение
этого уравнения для определения
соотношения между уравнением состояния
![]() и
выражением для внутренней энергии
и
выражением для внутренней энергии
![]() термодинамической
системы. Преобразуем выражение (4.4)
к следующему виду:
термодинамической
системы. Преобразуем выражение (4.4)
к следующему виду:
 .
(4.5) Здесь учтено, что
внутренняя энергия
.
(4.5) Здесь учтено, что
внутренняя энергия
![]() является
функцией состояния, и поэтому она имеет
полный дифференциал:
является
функцией состояния, и поэтому она имеет
полный дифференциал:
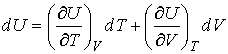 .
(4.6) С другой стороны,
так как энтропия
.
(4.6) С другой стороны,
так как энтропия
![]() тоже
является функцией состояния, для ее
полного дифференциала можно записать
выражение:
тоже
является функцией состояния, для ее
полного дифференциала можно записать
выражение:
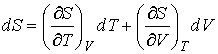 .
(4.7) Сопоставление
формул (4.5)
и (4.7)
дает
.
(4.7) Сопоставление
формул (4.5)
и (4.7)
дает
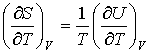 ,
(4.8)
,
(4.8)
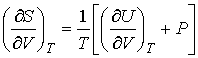 .
(4.9) Далее, учитывая
то, что
.
(4.9) Далее, учитывая
то, что
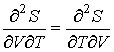 (4.10) и дифференцируя
по
(4.10) и дифференцируя
по
![]() выражение
(4.8)
и по
выражение
(4.8)
и по
![]() выражение
(4.9),
имеем:
выражение
(4.9),
имеем:
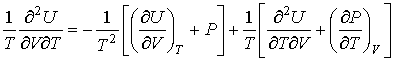 .
(4.11) Использование
равенства
.
(4.11) Использование
равенства
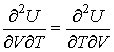 (4.12) позволяет получить
окончательное выражение для
дифференциального уравнения, связывающего
уравнение состояния
(4.12) позволяет получить
окончательное выражение для
дифференциального уравнения, связывающего
уравнение состояния
![]() и
внутреннюю энергию
и
внутреннюю энергию
![]() термодинамической
системы
термодинамической
системы
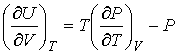 .
(4.13)
.
(4.13)

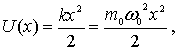
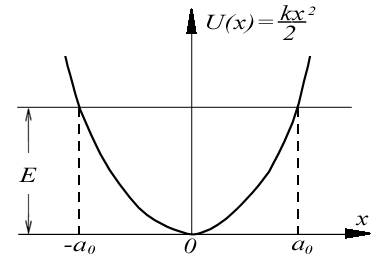
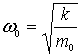 -
собственная частота классического
гармонического осциллятора. Таким
образом, квантово-механическая задача
о гармоническом осцилляторе сводится
к задаче о движении частицы в
параболической потенциальной
яме (4.77)
. Рассмотрим сначала
поведение классического гармонического
осциллятора. Пусть частица с полной
энергией
-
собственная частота классического
гармонического осциллятора. Таким
образом, квантово-механическая задача
о гармоническом осцилляторе сводится
к задаче о движении частицы в
параболической потенциальной
яме (4.77)
. Рассмотрим сначала
поведение классического гармонического
осциллятора. Пусть частица с полной
энергией
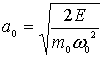 . В
квантовой механике для решения задачи
о гармоническом осцилляторе нужно
решить уравнение Шредингера (4.6)
с потенциальной энергией (4.77)
. В
квантовой механике для решения задачи
о гармоническом осцилляторе нужно
решить уравнение Шредингера (4.6)
с потенциальной энергией (4.77)