2.3 Собственный базис симметричной матрицы

В п. 1.3 главы 1 был рассмотрен алгоритм получения собственных векторов матрицы А. Мы увидели, что для некоторых матриц совокупность их собственных векторов образует базис пространства , а для иных нет. Возникает вопрос: какой должна быть квадратная матрица, чтобы из ее собственных векторов всегда можно было построить базис всего пространства . Таким свойством обладает симметричная матрица – квадратная матрица, у которой элементы, симметричные относительно главной диагонали равны, т.е. , т.е. .

Пусть

– симметричная матрица, т.е. , для всех .

Теорема 1. Характеристический многочлен симметричной матрицы А имеет ровно n вещественных корней ₁, ₂, …, _n с учетом их кратности.

Как мы знаем, корни ₁, …, _n, и только они, являются собственными числами матрицы А. Напомним, что для произвольной матрицы А порядка n характеристический многочлен может иметь меньше чем n вещественных корней или не иметь их вовсе.

Известно, что для произвольной квадратной матрицы, собственные векторы, отвечающие различным собственным значениям, линейно независимы. Для симметричной матрицы имеет место более сильное утверждение.

Теорема 2. Собственные векторы симметричной матрицы, отвечающие различным собственным значениям, попарно ортогональны.

Действительно, пусть , , , . Покажем, что и ортогональны, т.е. .

Нам понадобится следующее свойство скалярного произведения: для любых и любой квадратной матрицы В:

.

Рассмотрим скалярное произведение .

;

; .

Отсюда ; , так как , то , что и требовалось проверить.

В благоприятном случае, если все собственные значения ₁, ₂,…,_n симметричной матрицы различны, то соответствующие собственные векторы по теореме 2 попарно ортогональны и образуют ортогональный базис в . (см. пример 1, § 1.3 гл. 1). Оказывается, и в общем случае, симметричная матрица обладает набором собственных векторов, образующих ортогональный базис в . Этот факт основан на теореме.

Теорема 3. Пусть  – корень кратности р характеристического многочлена симметричной матрицы А, и – собственное подпространство, отвечающее корню . Тогда размерность подпространства равна кратности корня : .

Отметим, что для несимметричной матрицы может оказаться, что и из собственных векторов матрицы нельзя составить базис . (см. пример 3, п. 1.3, гл. 1).

Из сформулированных теорем следует важное утверждение.

Теорема 4. Для симметричной матрицы существует ортогональный базис, составленный из ее собственных векторов.

Опишем теперь процесс получения ортогонального (даже ортонормированного) базиса из собственных векторов симметричной матрицы.

1. Вычислим корни характеристического многочлена .

Пусть – различные корни кратности соответственно . Все корни вещественны и .

2. Каждый корень подставим в систему уравнений

.

Найдем фундаментальную систему решений (ФСР) собственного подпространства . Число векторов ФСР обязательно равно р_к – кратности корня _к. Система векторов ФСР , отвечающие одному и тому же _к, может оказаться не ортогональной.

3. Применим к системе процесс ортогонализации (в случае необходимости). Получим новую фундаментальную систему , уже ортогональную.

4. Объединим все найденные системы , отвечающие различным собственным числам _к . В результате получим ортогональную систему из n собственных векторов матрицы А (различным _к отвечают ортогональные собственные векторы), которая и образует базис в – собственный ортогональный базис матрицы А: .

5. Нормируем этот базис: .

Получим ортонормированный собственный базис (см. умения) симметричной матрицы А.

Заметим, что матрица С перехода от стандартного базиса к собственному базису – ортогональна. Теперь сформулируем еще один важный результат. Для всякой симметричной матрицы А существует такая ортогональная матрица U, что , причем В имеет диагональный вид: 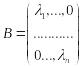, где _i – собственные числа матрицы А, . (В качестве матрицы U следует взять ортогональную матрицу перехода С).