Приложение 2 о приближенном вычислении собственных значений матрицы

Нахождение собственных значений и собственных векторов матриц требуется во многих физических и технических задачах при исследовании устойчивости различных процессов, например при определении устойчивости и колебаний различных инженерных сооружений.

Задачу отыскания всех собственных значений и собственных векторов матрицы называют полной проблемой собственных значений, а нахождение лишь некоторых из них – частичной проблемой собственных значений.

Задача численного нахождения собственных значений и векторов является одной из наиболее сложных вычислительных задач алгебры.

Как известно, собственные значения  матрицы А являются корнями характеристического многочлена det(A–E). Может показаться, что основная трудность состоит в отыскании корней этого многочлена, однако, для произвольной матрицы, особенно большого размера, затруднительно вычислить сами коэффициенты характеристического многочлена. Поэтому большинство численных методов основываются не на получении характеристического многочлена матрицы А, а на различных преобразованиях, упрощающих матрицу.

В практических задачах чаще всего требуется вычислить не все собственные значения, а лишь некоторые из них. Так, в вопросах устойчивости требуется найти минимальное (или максимальное) по модулю собственное значение матрицы.

Для этого проще всего использовать итерационные методы. Опишем такой алгоритм для нахождения максимального по модулю собственного значения и соответствующего собственного вектора.

Пусть матрица А порядка n имеет все действительные собственные значения ₁, ₂, …, _n и соответствующие собственные векторы которые образуют базис в . Предположим, что собственные значения удовлетворяют условиям:

т.е.

собственные значения монотонно убывают по модулю, причем ₁ – максимальное значение (строго больше остальных).

Возьмем произвольный вектор (начальное приближение), разложим его по базису {u}

Умножим теперь матрицу А на вектор , в результате получим вектор

или коротко

А теперь умножим матрицу А на вектор и получим вектор

Продолжая процесс, через k шагов получим

Преобразуем полученное равенство:

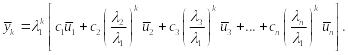
Так как то

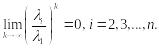
Это означает, что при больших k слагаемые 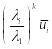в разложении вектора убывают и не играют существенной роли, а значит, вектор будет “почти” коллинеарен вектору .

, т.е. .

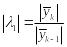Приведенные рассуждения положены в основу итерационного метода нахождения наибольшего по модулю собственного значения. Этот метод носит название степенного метода. При достаточно большом ₁ длины полученных векторов сильно растут, поэтому при реализации алгоритма обычно проводят нормировку .

Алгоритм степенного метода состоит в следующем:

1. Задается начальное приближение

2. Последовательно вычисляются по формулам:

k-й шаг итерации

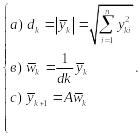
3. Вычисление ведется до тех пор, пока не станет где e - заданная точность.

4. Собственный вектор

Это означает, что последовательность длин d_k векторов сходится к максимальному собственному значению ₁, а последовательность векторов к собственному вектору , отвечающему собственному значению ₁.

Отметим, что скорость сходимости степенного метода зависит от того, насколько _max превышает остальные собственные значения, чем больше отношение тем быстрее сходится метод.

Так, для матрицы

точное значение _max = 10,123, _min = 1,887. Уже на третьем шаге итерации получаем

₁ d₃ = 10,125,

что дает хорошее приближение для ₁.

Если наибольшее по модулю собственное значение имеет кратность больше единицы, то итерационный процесс сходится к одному из собственных векторов собственного подпространства . Выбирая различные начальные векторы , можно построить все линейно независимые собственные векторы подпространства .

Если же нужно найти не наибольшее, а наименьшее собственное значение , то следует использовать соображение: если – собственный вектор А с собственным значением , то

Таким образом вектор u является собственным и для матрицы А^–1, отвечающим собственному значению

Отсюда следует, что

Значит, для нахождения минимального собственного значения матрицы А следует найти обратную матрицу А^–1 и для нее найти максимальное собственное значение.