4.4 Матрица перехода

Как мы видим в рассмотренных примерах, в линейном пространстве V все базисы равноправны. Тот или иной базис выбирают исходя из конкретных обстоятельств. Иногда для представления элементов линейного пространства используют несколько базисов и тогда возникает задача о преобразовании координат векторов, которые связаны с изменением базиса. Мы уже встречались с этой задачей в пространстве Rⁿ (при переходе от стандартного базиса к собственному базису матрицы А).

Матрицей перехода от базиса к базису в линейном n-мерном пространстве V называется квадратная матрица С порядка n, столбцами которой являются координаты нового базиса по старому :

, .

Сформулируем еще раз основные свойства матрицы перехода С.

1. Матрица С невырождена и имеет обратную .

2. Матрица является матрицей перехода от нового базиса к старому .

3. Пусть в n-мерном линейном пространстве задан базис ; С – произвольная невырожденная квадратная матрица порядка n, тогда существует такой базис в линейном пространстве, что матрица С будет матрицей перехода от базиса к базису . Действительно, так как С – невырождена, то ее вектор-столбцы линейно независимы. Будем считать столбцы матрицы С координатами по базису новой системы из n линейно независимых векторов , тогда система – базис, а матрица С – матрица перехода от к .

4. Если в линейном пространстве заданы базисы , и , причем С – матрица перехода от базиса к , а В – матрица перехода от базиса к , то матрица–произведение является матрицей перехода от базиса к .

Например, пусть векторы “нового” базиса трехмерного линейного пространства выражены через “старый” базис по формулам:

,

,

.

Чтобы составить матрицу С перехода от к , запишем координаты векторов системы по базису в столбцы матрицы С:

, , .

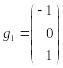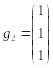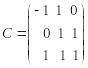Матрица С невырожденная, . Матрица имеет вид:

.

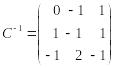Следовательно, соотношения, выражающие векторы базиса через векторы :

,

,

.

Рассмотрим теперь, как преобразуются координаты произвольного вектора в линейном пространстве V при переходе от старого базиса к новому с заданной матрицей перехода С.

Мы уже подробно рассматривали эту задачу в случае арифметического n-мерного пространства Rⁿ. Аналогичный результат имеет место в случае произвольного линейного пространства V, а именно: пусть старый и новый –два базиса в n-мерном пространстве V; С – матрица перехода от к ; v – произвольный вектор пространства V;

и , тогда , т.е. чтобы получить координаты вектора в старом базисе нужно столбец координат этого вектора в новом базисе умножить слева на матрицу перехода из старого базиса в новый.

4.5 Подпространство

В любом линейном пространстве V можно выделить такое подмножество, которое относительно операций из V само является линейным пространством.

Определение. Непустое подмножество W V называется подпространством линейного пространства V, если:

1) сумма любых векторов х, у из W является вектором из W, т.е. если ;

2) произведение любого вектора х из W на скаляр есть вектор из W, т.е. если , где – число.

Иными словами, применение линейных операций к векторам подмножества W не выводит результат из W, говорят, что подпространство замкнуто относительно операций сложения и умножения на скаляр. Фактически подпространство W является пространством, а потому, основные понятия, введенные для пространств, переносятся на подпространства. Так, базис подпространства W – система линейно независимых векторов такая, что любой вектор представим в виде линейной комбинации .

Доказывается, что все базисы подпространства состоят из одного и того же числа векторов m, которое называется размерностью подпространства W и обозначается .

Рассмотрим примеры подпространств.

Множество, состоящее только из нулевого вектора , есть подпространство в V и все пространство V также есть подпространство самого себя. Эти два подпространства называют несобственными, остальные же подпространства – собственные.

1. Пусть в пространстве задан фиксированный вектор . Рассмотрим множество W векторов из , ортогональных вектору а:

.

Покажем, что W – подпространство. Действительно, пусть , , т.е. их скалярные произведения с вектором а равны нулю: , . Рассмотрим вектор , проверим, принадлежит ли он W, т.е.равно ли скалярное произведение нулю:

,

аналогично, для и любого числа а верно:

,

т.е. W – подпространство.

Распишем координатное равенство :

.

Геометрически это уравнение определяет любую плоскость (так как а – произвольно), проходящую через начало координат. Размерность (плоскость двумерна).

Заметим, что любая плоскость и прямая, проходящие через начало координат в пространстве , являются подпространствами в . Других собственных подпространств в нет.

2. Множество решений системы линейных однородных уравнений, , где является подпространством , причем , где .

3. В пространстве непрерывных на функций множество всех дифференцируемых функций образует подпространство (так как производная суммы функций равна сумме производных, а константу можно выносить за знак производной).

4. В пространстве многочлены степени образуют пространство. Совокупность же многочленов фиксированной степени n подпространством не является (легко проверить).

5. В пространстве квадратных матриц порядка n все симметричные матрицы образуют подпространство.

6. В том же пространстве можно выделить подпространство верхнетреугольных (нижнетреугольных) матриц.

Легко проверить, что все рассмотренные пространства содержат нулевой элемент и, вместе с каждым элементом х подпространства, противоположный элемент – х. Этот факт является общим для всех подпространств (следует из определения).

Рассмотрим теперь множество решений неоднородной системы линейных уравнений , , , . Мы знаем, что общее решение этой системы записывается в виде:

,

где – общее решение однородной системы, а – частное решение неоднородной системы (любое). Множество решений неоднородной системы устроено так: надо взять подпространство решений однородной системы и “сдвинуть” его на произвольный вектор – решение неоднородной системы. Это множество не является подпространством (например, нуль-вектор в него не входит).

В пространстве мы приводили примеры подпространств – плоскости и прямые, проходящие через начало координат. В то же время, плоскости или прямые, не проходящие через начало координат, не являются подпространствами, но по своим свойствам похожи на соответствующие подпространства. Они получены параллельным сдвигом в пространстве.

Пусть W – подпространство пространства V, а – фиксированный вектор, вообще говоря, не принадлежащий W. Тогда совокупность Н всех таких векторов х, что , где у – пробегает все подпространство W, называют сдвигом подпространства W. Множество Н, вообще говоря, не является подпространством.

Важным примером подпространства является линейная оболочка векторов.

Определение. Пусть – система векторов из пространства V. Совокупность всех линейных комбинаций , где – действительные числа, называется линейной оболочкой системы векторов . Обозначим линейную оболочку .

Примеры.

1. Линейная оболочка векторов базиса пространства V совпадает со всем пространством.

2. Рассмотрим систему функций из пространства . Их линейная оболочка – множество всех многочленов степени .

Легко проверить, что линейная оболочка векторов , образует подпространство, так как при сложении линейных комбинаций и умножении их на число вновь получаются линейные комбинации так же векторов.

Для линейной оболочки , если же линейно независимы, то они служат базисом в L и . Если векторы , порождающие линейную оболочку, линейно зависимы, то , где r – ранг системы векторов (максимальное число линейно независимых векторов системы). Всякий базис можно дополнить до базиса всего пространства V.

Рассмотрим еще один пример.

В пространстве линейную оболочку векторов составляют функции вида , где a, b – любые вещественные числа. Функции линейно независимы и составляют базис своей линейной оболочки, . Найдем, например, координаты гиперболических функций и в этом базисе.

, ,

поэтому координаты , а в базисе .